Funciones de grado superior a dos (ejemplos)

Una función (polinómica) de grado superior a dos tiene la forma general:

f(x) = a₀ + a₁x +a₂x² + ….a_nxⁿ

Con n = 3, 4, 5, …, un entero no negativo y los coeficientes a_o, a₁… a_n, que usualmente son números reales.

El grado de la función viene dado por el valor de n, el mayor de los exponentes y que a su vez es mayor que 2. Cuando n = 0 es una función constante, si n= 1 se trata de una función lineal, y finalmente con n = 2 es una función cuadrática.

Ejemplos de funciones de grado superior a dos, en la variable “x”, son las siguientes:

• f (x) = x³
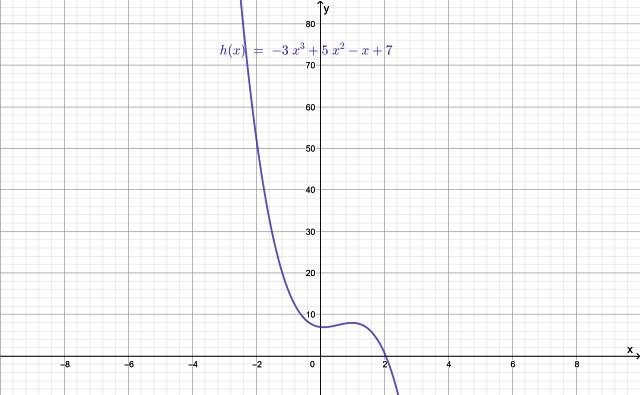
• h (x) = − 3x³ + 5x² – x + 7
• g (x) = x⁴ − 6x² + 25

La función f(x) = x³ es la más sencilla de todas las funciones de grado superior a dos y su grado es 3. A una función de grado 3 se la conoce también como función cúbica. Por su parte, g(x) es de grado 4, por ser 4 el máximo exponente.

El valor de n es muy importante porque determina la forma general de la gráfica, y asimismo la cantidad máxima de raíces o intersecciones que la función tiene con el eje horizontal. En efecto, una función de grado 3 tocará al eje horizontal a lo sumo en 3 puntos, una de grado 4 lo hará a lo sumo en 4 puntos y así sucesivamente.

En cuanto al término independiente, en una función polinómica de cualquier grado indica la intersección de la función con el eje vertical.

Características de las funciones polinómicas de grado superior a dos

Dominio

El dominio de una función es el conjunto de valores que permiten calcular los valores de y = f(x). Para las funciones polinómicas este conjunto es el de los números reales R, o bien el conjunto de los números complejos, de ser necesario extender el dominio.

Quiere decir que, dada la función polinómica f(x) = a₀ + a₁x +a₂x² + ….a_nxⁿ, siempre se puede sustituir en ella cualquier número real, efectuar las operaciones indicadas y obtener como resultado un valor de y=f(x) real.

Rango

Es el conjunto formado por todos los valores que adquiere f(x), es decir, las imágenes que tiene cada valor de x a través de la función f(x). Para las funciones polinómicas de grado mayor a 2, este conjunto es el de los números reales.

Raíces de la función

Son los valores de x para los cuales se cumple que f(x) = 0. Como se indicó anteriormente, el grado de la función señala el número máximo de raíces que esta puede tener, aunque no todas ellas son necesariamente reales.

Cuando los coeficientes de la función son números reales, las raíces reales corresponden a las intersecciones de la función con el eje x.

Ejemplo 1

Las raíces racionales de la función f (x) = 2x³ − 9x² + 7x + 6 se pueden encontrar mediante el siguiente teorema:

Si la raíz de f(x) = a₀ + a₁x +a₂x² + ….a_nxⁿ es de la forma b/c, entonces los valores posibles de b son factores de a_o y los valores posibles de c son factores de a_n.

Para la función del ejemplo, las combinaciones ya simplificadas son:  ±  6, ± 3, ±  2, ±  1, ±  3/2, ±  ½. Ahora se va probando cada una mediante el procedimiento de división sintética, por ejemplo. Cuando el residuo de la división es 0, el valor probado es una raíz:

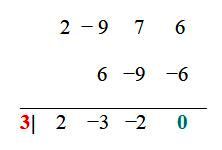
El valor x₁ = 3 es una raíz o cero de la función, por lo tanto (x−3) es un factor común de f(x), y esta se puede escribir como:

f(x) = (x−3)∙(2x² −3x −2)

Las dos raíces restantes son los valores que satisfacen la ecuación 2x² −3x −2 = 0. Esta ecuación se puede resolver mediante la fórmula general, una calculadora científica o repitiendo el proceso de tanteo anterior.

Dichas raíces son x₂ = 2 y x₃ = − ½, y ahora f(x) se puede escribir como el producto de tres factores:

f(x) = (x−3)∙(x−2)⋅(x + ½)

Las intersecciones de f(x) con el eje x son los puntos: P₁ (3,0), P₂(2,0) y P₃(−½,0). La gráfica de la función, obtenida con Geogebra, muestra sus intersecciones con el eje x:

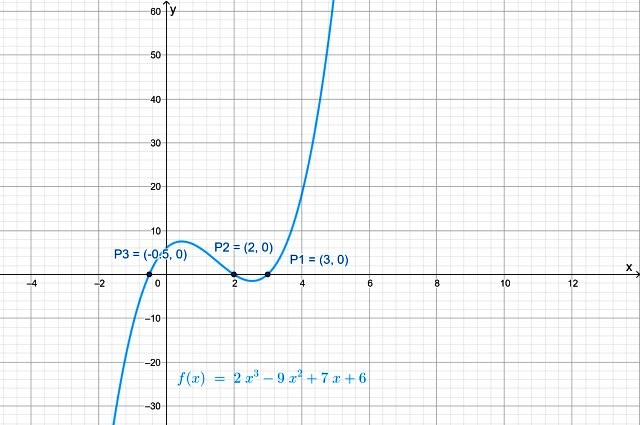
Intersección con el eje vertical

Para hallar la intersección de la función con el eje vertical hay que encontrar f(0), que es simplemente a₀.

Ejemplo 2

Hallar la intersección de f(x) = 2x³ − 9x² + 7x + 6 con el eje vertical es muy simple, al hacer x = 0 en f(x) se obtiene:

f(x) = 6

Y el punto de intersección de la función con el eje vertical es P₄(0,6).

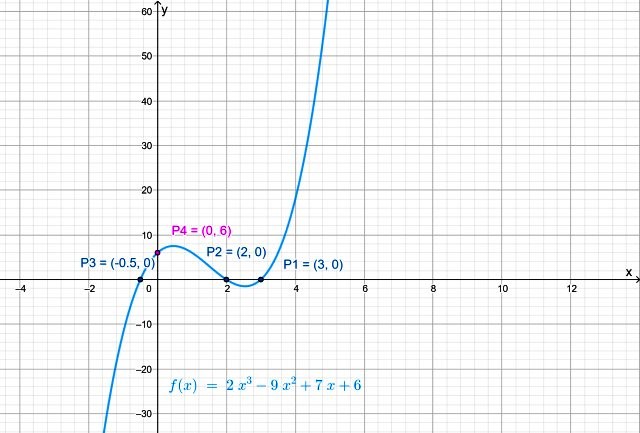
Continuidad

Las funciones polinómicas en general, y en particular las de grado superior a 2 son funciones continuas en todo su dominio, esto significa que no tienen saltos, escalones, agujeros o valores para los cuales no estén definidas. Tampoco tienen asíntotas, que son rectas verticales, horizontales u oblicuas a las cuales la función se acerca sin cruzarlas.

Estas cualidades de suavidad y continuidad se aprecian en las gráficas mostradas anteriormente.

Gráfica de las funciones de grado superior a 2

Las gráficas de las funciones de grado superior a 2 son continuas y suaves, y su forma depende del grado del polinomio.

Por ejemplo, las de grado 3 semejan una letra “n” y las de grado 4 una “w”, aunque si se invierten los signos de los coeficientes la forma de la gráfica cambia (comparar las figuras 2 y 1, ya que esta última tiene signo negativo en el término con el mayor grado).

Para valores de x alejados de x = 0, tanto a la izquierda como a la derecha, la función se comporta a como lo haría el término de mayor grado, porque este prevalece sobre los demás cuando x se hace muy grande o muy pequeño.

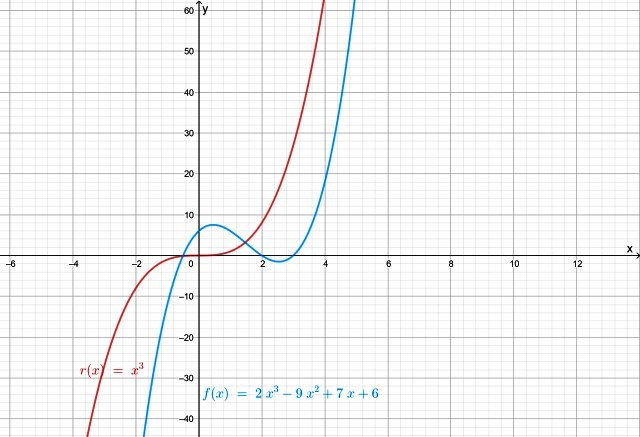
En la imagen que sigue se compara la función f (x) = 2x³ − 9x² + 7x + 6 con la función r (x) = x³ y se aprecia que la forma de ambas curvas es parecida para valores de x que estén bien lejos de x = 0.

Para valores grandes de x la función crece rápidamente tendiendo a +∞, mientras que para valores negativos de x, la función decrece rápidamente y tiende a −∞.

Comparando las curvas de grado par (figura 4) con las de grado impar (figura 2), siempre y cuando el coeficiente que acompaña al término de mayor grado tenga el mismo signo, se observa que las curvas de grado impar empiezan desde “y” negativo y van creciendo, mientras que las de grado par empiezan en “y” positivo y decrecen.

Referencias

1. Barnett, R. 2000. Precálculo: Funciones y gráficas. 4ta. Edición. McGraw Hill.
2. Cálculo.CC. Funciones Polinómicas. Recuperado de: calculo.cc.
3. Larson, R. 2012. Precálculo. 8va. Edición. Cengage Learning.
4. Stewart, J. 2007. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
5. Varsity Tutors. Graficando funciones polinomiales. Recuperado de: varsitytutors.com.