Valor presente neto: para qué sirve, cómo se calcula, ventajas
El valor presente neto (VPN) es la diferencia entre el valor presente de las entradas de efectivo y el valor presente de las salidas de efectivo durante un período de tiempo dado.
El valor presente neto se determina al calcular los costos (flujos de efectivo negativos) y los beneficios (flujos de efectivo positivos) para cada período de una inversión. El período suele ser de un año, pero podría medirse en trimestres o meses.

Es el cálculo utilizado para encontrar el valor presente de un flujo futuro de pagos. Representa el valor del dinero en el tiempo y se puede utilizar para comparar alternativas de inversión que sean similares. Se debe evitar cualquier proyecto o inversión con un VPN negativo.
Índice del artículo
- 1 Valor de los flujos de efectivo en el tiempo
- 2 ¿Para qué sirve el valor presente neto?
- 3 Cómo se calcula
- 4 Ventajas
- 5 Desventajas
- 6 Ejemplos
- 7 Referencias
El valor del dinero en el tiempo determina que el tiempo afecta el valor de los flujos de efectivo.
Por ejemplo, un prestamista puede ofrecer 99 centavos por la promesa de recibir $1 al mes siguiente. Sin embargo, la promesa de recibir ese mismo dólar dentro de 20 años en el futuro valdría hoy mucho menos para ese mismo prestamista, incluso si la retribución en ambos casos fuera igualmente cierta.
Esta disminución en el valor actual de los flujos de efectivo futuros se basa en la tasa de rentabilidad elegida, o tasa de descuento.
Por ejemplo, si existe una serie de flujos de efectivo idénticos en el tiempo, el flujo de efectivo en el presente es el más valioso, y cada flujo de efectivo futuro se hace menos valioso que el flujo de efectivo anterior.
Esto es porque el flujo presente se puede invertir de inmediato y así comenzar a obtener rentabilidad, mientras que con un flujo futuro no se puede.
Debido a su simplicidad, el valor presente neto es una herramienta útil para determinar si un proyecto o inversión resultará en una ganancia o en una pérdida neta. Un valor presente neto positivo resulta en ganancias, mientras que uno negativo da como resultado una pérdida.
El valor presente neto mide el exceso o el déficit de los flujos de efectivo, en términos del valor presente, por encima del costo de los fondos. En una situación teórica de presupuesto con capital ilimitado, una empresa debe realizar todas las inversiones con un valor presente neto positivo.
El valor presente neto es una herramienta central en el análisis del flujo de caja y es un método estándar para utilizar el valor del dinero en el tiempo para evaluar proyectos a largo plazo. Es ampliamente utilizado en economía, finanzas y contabilidad.
Se utiliza en la elaboración de presupuestos de capital y en la planificación de inversiones para analizar la rentabilidad de una inversión o proyecto planeado.
Supongamos que un inversionista pudiera elegir recibir un pago de $100 hoy o en un año. Un inversionista racional no estaría dispuesto a posponer el pago.
Sin embargo, ¿qué pasaría si un inversor pudiera elegir recibir $100 hoy o $105 en un año? Si el pagador es confiable, ese 5% adicional podría valer la pena la espera, pero solo si no hubiera otra cosa que los inversionistas pudieran hacer con los $100 que ganaran más del 5%.
Un inversionista podría estar dispuesto a esperar un año para ganar un 5% adicional, pero eso puede no ser aceptable para todos los inversionistas. En este caso, el 5% es la tasa de descuento que variará según el inversor.
Si un inversor supiera que podría ganar el 8% de una inversión relativamente segura durante el próximo año, no estaría dispuesto a posponer el pago del 5%. En este caso, la tasa de descuento del inversor es del 8%.
Una empresa puede determinar la tasa de descuento utilizando la rentabilidad esperada de otros proyectos con un nivel de riesgo similar, o el costo de pedir dinero prestado para financiar el proyecto.
Para calcular el valor presente neto se utiliza la siguiente fórmula que se muestra a continuación:

Rt= entrada o salida neta de efectivo en un solo periodo t.
i= tasa de descuento o rentabilidad que podría obtenerse en inversiones alternas.
t= número de períodos de tiempo.
Esta es una manera más fácil de recordar el concepto: VPN= (Valor presente de los flujos de efectivo esperados) – (Valor presente del efectivo invertido)
Además de la fórmula en sí, el valor presente neto se puede calcular utilizando tablas, hojas de cálculo, o calculadoras.
El dinero en el presente vale más que la misma cantidad en el futuro, debido a la inflación y a las ganancias de inversiones alternas que podrían hacerse durante el tiempo intermedio.
En otras palabras, un dólar que se gane en el futuro no valdrá tanto como uno ganado en el presente. El elemento de tasa de descuento de la fórmula de valor presente neto es una forma de tenerlo en cuenta.
– Toma en cuenta el valor del dinero en el tiempo, poniendo énfasis en los flujos de efectivo anteriores.
– Observa todos los flujos de efectivo involucrados a lo largo de la vida del proyecto.
– El uso del descuento reduce el impacto de los flujos de efectivo menos probables a largo plazo.
– Tiene un mecanismo de toma de decisiones: rechazar proyectos con valor presente neto negativo.
El valor presente neto es un indicador de cuánto valor agrega una inversión o proyecto a la empresa. En teoría financiera, si hay una opción entre dos alternativas mutuamente excluyentes, se debe seleccionar la que produzca el valor presente neto más alto.
Podrían aceptarse proyectos con un riesgo adecuado si tienen un valor presente neto positivo. Esto no significa necesariamente que deban llevarse a cabo, ya que el valor presente neto al costo del capital puede no tener en cuenta el costo de oportunidad, es decir, la comparación con otras inversiones disponibles.
Se supone que una inversión con un valor presente neto positivo será rentable, y una inversión con uno negativo dará lugar a una pérdida neta. Este concepto es la base de la regla del valor presente neto, que establece que solo deben considerarse las inversiones con valores de VPN positivos.
Un valor presente neto positivo indica que las ganancias planeadas que son generadas por un proyecto o inversión, en dólares presentes, exceden los costos proyectados, también en dólares presentes.
Un inconveniente del uso de un análisis de valor presente neto es que hace suposiciones sobre eventos futuros que pueden no ser confiables. La medición de la rentabilidad de una inversión con el valor presente neto se basa en gran medida en estimaciones, por lo que puede haber un margen sustancial para el error.
Entre los factores estimados están el costo de inversión, la tasa de descuento y los rendimientos esperados. Un proyecto puede requerir gastos imprevistos para arrancar o puede requerir gastos adicionales al final del proyecto.
El período de recuperación, o método de recuperación, es una alternativa más simple al valor presente neto. Este método calcula el tiempo que tardará en reembolsarse la inversión original.
Sin embargo, este método no tiene en cuenta el valor del dinero en el tiempo. Por esta razón, los períodos de recuperación calculados para inversiones a largo plazo tienen mayor potencial de inexactitud.
Además, el período de recuperación está estrictamente limitado a la cantidad de tiempo requerido para recuperar los costos iniciales de inversión. Es posible que la tasa de retorno de la inversión experimente movimientos bruscos.
Las comparaciones que usan períodos de recuperación no tienen en cuenta la rentabilidad a largo plazo de inversiones alternas.
Supongamos que una empresa puede invertir en equipos que costarán $1.000.000, y se espera que generen ingresos de $25.000 mensuales por 5 años.
La compañía tiene el capital disponible para el equipo. Alternativamente, podría invertirlo en el mercado de valores para obtener un rendimiento esperado del 8% anual.
Los gerentes sienten que comprar un equipo o invertir en el mercado de valores son riesgos similares.
Como el equipo se paga por adelantado, este es el primer flujo de efectivo incluido en el cálculo. No hay tiempo transcurrido que deba contabilizarse, por lo que la salida de $1.000.000 no necesita ser descontada.
Identificar el número de períodos (t)
Se espera que el equipo genere un flujo de efectivo mensual y que dure 5 años. Esto significa que habrá 60 flujos de efectivo y 60 períodos incluidos en el cálculo.
Identificar la tasa de descuento (i)
Se espera que la inversión alterna pague el 8% anual. Sin embargo, debido a que el equipo genera un flujo mensual de efectivo, la tasa de descuento anual debe convertirse en una tasa mensual. Usando la siguiente fórmula, se encuentra que:
Tasa mensual de descuento= ((1+0,08)1/12)-1= 0,64%.
Los flujos mensuales de efectivo se obtienen al final del mes. El primer pago llega exactamente un mes después de haber comprado el equipo.
Este es un pago futuro, por lo que debe ajustarse por el valor del dinero en el tiempo. Para ilustrar el concepto, en la tabla a continuación se descuentan los primeros cinco pagos.
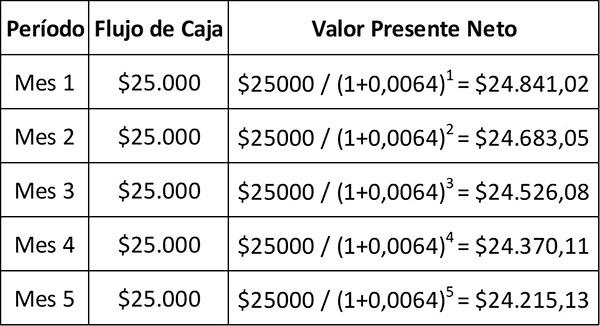
El cálculo completo del valor presente neto es igual al valor presente de los 60 flujos de efectivo futuros, menos la inversión de $1.000.000.
El cálculo podría ser más complicado si se esperara que el equipo tuviera algún valor al final de su vida útil. Sin embargo, en este ejemplo, se supone que no va a valer nada.
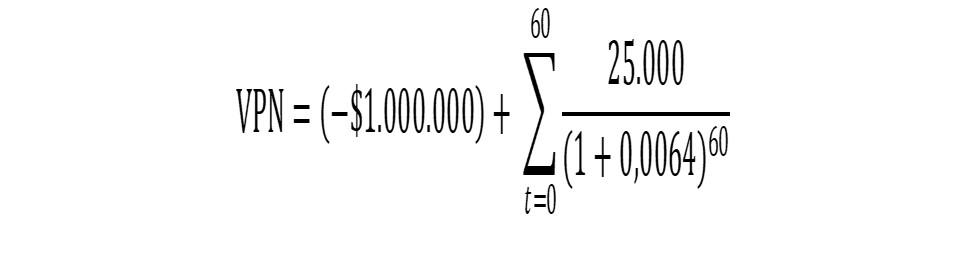
Esta fórmula se puede simplificar al siguiente cálculo: VPN = (-$1.000.000) + ($1.242.322,82) = $242.322,82
En este caso, el valor presente neto es positivo. Por tanto, el equipo debe ser comprado. Si el valor presente de estos flujos de efectivo hubiera sido negativo debido a que la tasa de descuento fuera mayor, o los flujos de efectivo netos fueran menores, se habría evitado la inversión.
- Will Kenton (2018). Net Present Value – NPV. Investopedia. Tomado de: investopedia.com.
- Wikipedia, the free encyclopedia (2019). Net present value. Tomado de: en.wikipedia.org.
- CFI (2019). What is Net Present Value (NPV)? Tomado de: corporatefinanceinstitute.com.
- Tutor2u (2019). Net Present Value (“NPV”) Explained. Tomado de: tutor2u.net.
- Investing Answers (2019). Net Present Value (NPV). Tomado de: investinganswers.com.
- Ellen Chang (2018). What Is Net Present Value and How Do You Calculate It? The Street. Tomado de: thestreet.com.
