Coeficiente de determinación: fórmulas, cálculo, interpretación, ejemplos
El coeficiente de determinación es un número comprendido entre 0 y 1 que representa la fracción de puntos (X,Y) que siguen la línea de ajuste por regresión de un conjunto de datos con dos variables.
También se le conoce como bondad del ajuste y se le denota por R2. Para calcularlo se toma el cociente entre la varianza de los datos Ŷi estimados por el modelo de regresión y la varianza de los datos Yi correspondientes a cada Xi de los datos.
R2 = Sŷ / Sy

Si el 100% de los datos están sobre la línea de la función de regresión, entonces el coeficiente de determinación será 1.
Por el contrario, si para un conjunto de datos y cierta función de ajuste el coeficiente R2 resultase ser igual a 0.5, entonces puede decirse que el ajuste es satisfactorio o bueno en un 50%.
De manera similar, cuando el modelo de regresión arroja valores de R2 inferiores a 0.5, ello indica que la función de ajuste elegida no se adapta satisfactoriamente a los datos, siendo por lo tanto necesario buscar otra función de ajuste.
Y cuando la covarianza o el coeficiente de correlación tiende a cero, entonces las variables X e Y de los datos no guardan relación alguna, y por tanto R2 también tenderá a cero.
Índice del artículo
En la sección anterior se dijo que el coeficiente de determinación se calcula encontrando el cociente entre las varianzas:
-Estimada por la función de regresión de la variable Y
-La de la variable Yi correspondiente a cada una de la variable Xi de los N pares datos.
Dicho en forma matemática, queda así:
R2 = Sŷ / Sy
De esta fórmula se desprende que R2 representa la proporción de varianza explicada por el modelo de regresión. Alternativamente, puede calcularse R2 mediante la siguiente fórmula, totalmente equivalente a la anterior:
R2 = 1 – (Sε / Sy)
Donde Sε representa la varianza de los residuos εi = Ŷi – Yi , mientras que Sy es la varianza del conjunto de valores Yi de los datos. Para determinar Ŷi se aplica la función de regresión, lo que significa afirmar que Ŷi = f(Xi).
La varianza del conjunto de datos Yi, con i de 1 a N se calcula de esta manera:
Sy = [Σ (Yi –
Y después se procede en forma similar para Sŷ o para Sε.
A modo de mostrar el detalle de la forma como se hace el cálculo del coeficiente de determinación tomaremos el siguiente conjunto de cuatro pares de datos:
(X, Y): {(1, 1); (2, 3); (3, 6) y (4, 7)}.
Se propone un ajuste de regresión lineal para este conjunto de datos que se obtiene mediante el método de los mínimos cuadrados:
f(x) = 2.1 x – 1
Aplicando esta función de ajuste, se obtienen los pares:
(X, Ŷ): {(1, 1.1); (2, 3.2); (3, 5.3) y (4, 7.4)}.
Luego calculamos la media aritmética para X e Y:
Varianza Sy
Sy = [(1 – 4.25)2 + (3 – 4.25)2 + (6 – 4.25)2 +…. ….(7 – 4.25)2] / (4-1)=
= [(-3.25)2+ (-1.25)2 + (1.75)2 + (2.75)2) / (3)] = 7.583
Varianza Sŷ
Sŷ = [(1.1 – 4.25)2 + (3.2 – 4.25)2 + (5.3 – 4.25)2 +…. ….(7.4 – 4.25)2] / (4-1)=
= [(-3.25)2 + (-1.25)2 + (1.75)2 + (2.75)2) / (3)] = 7.35
Coeficiente de determinación R2
R2 = Sŷ / Sy = 7.35 / 7.58 = 0.97
El coeficiente de determinación para el caso ilustrativo considerado en el segmento anterior resultó ser 0.98. Es decir que el ajuste lineal mediante la función:
f(x) = 2.1x – 1
Es 98% confiable para explicar la data con la que se obtuvo mediante el método de mínimos cuadrados.
Además del coeficiente de determinación, existe el coeficiente de correlación lineal o también conocido como coeficiente de Pearson. Este coeficiente, denotado como r, se calcula mediante la siguiente relación:
r = Sxy / (Sx Sy)
Aquí el numerador representa la covarianza entre las variables X e Y, mientras que el denominador es el producto de la desviación estándar para la variable X y la desviación estándar para la variable Y.
El coeficiente de Pearson puede tomar valores entre -1 y +1. Cuando este coeficiente tiende a +1 hay correlación lineal directa entre X e Y. Si en cambio tiende a -1, hay correlación lineal pero cuando X crece Y decrece. Finalmente, es cercano a 0 no hay correlación entre las dos variables.
Es preciso destacar que el coeficiente de determinación coincide con el cuadrado del coeficiente de Pearson, solamente cuando el primero se ha calculado en base a un ajuste lineal, pero esta igualdad no es válida para otros ajustes no lineales.
Un grupo de estudiantes de bachillerato se proponen determinar una ley empírica para el periodo de un péndulo como función de su longitud. Para lograr este objetivo realizan una serie de mediciones en las que miden el tiempo de una oscilación del péndulo para diferentes longitudes obteniendo los siguiente valores:
| Longitud (m) | Período (s) |
|---|---|
| 0,1 | 0,6 |
| 0,4 | 1,31 |
| 0,7 | 1,78 |
| 1 | 1,93 |
| 1,3 | 2,19 |
| 1,6 | 2,66 |
| 1,9 | 2,77 |
| 3 | 3,62 |
Se pide realizar un gráfico de dispersión de los datos y realizar un ajuste lineal mediante regresión. Además, mostrar la ecuación de regresión y su coeficiente de determinación.
Solución

Puede observarse un coeficiente de determinación bastante alto (95%), por lo que se pudiese pensar que el ajuste lineal es óptimo. Sin embargo, si se observan los puntos en conjunto, parece que tienen tendencia a curvarse hacia abajo. Este detalle no está contemplado en el modelo lineal.
Para los mismos datos del ejemplo 1, realizar un gráfico de dispersión de los datos. En esta oportunidad, a diferencia del ejemplo 1, se pide hacer un ajuste por regresión mediante una función potencial.
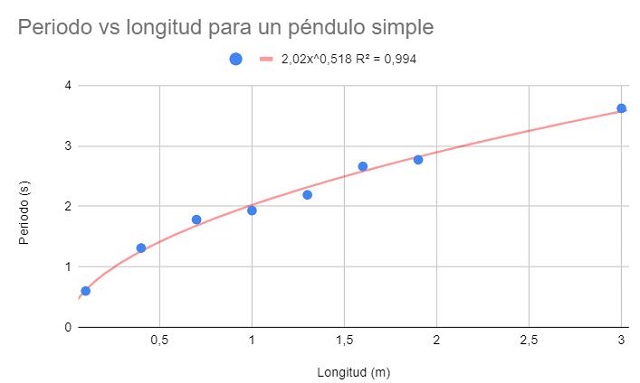
También muestre la función de ajuste y su coeficiente de determinación R2.
Solución
La función potencial es de la forma f(x) = AxB, donde A y B son constantes que se determinan por método de mínimos cuadrados.
La figura anterior muestra la función potencial y sus parámetros, así como el coeficiente de determinación con un valor altísimo de 99%. Note que los datos siguen la curvatura de la línea de tendencia.
Con los mismos datos del ejemplo 1 y ejemplo 2, realice un ajuste polinomial de segundo grado. Mostrar el gráfico, el polinomio de ajuste y el coeficiente de determinación R2 correspondiente.
Solución
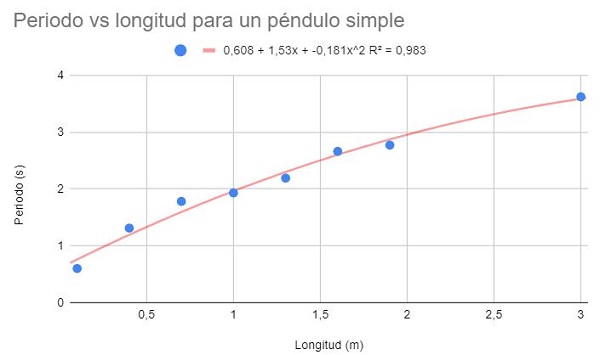
Con el ajuste polinómico de segundo grado puede verse una línea de tendencia que se ajusta bien a la curvatura de los datos. Asimismo, el coeficiente de determinación está por encima del ajuste lineal y por debajo del ajuste potencial.
De los tres ajustes mostrados, el que tiene un coeficiente de determinación más alto es el ajuste potencial (ejemplo 2).
El ajuste potencial coincide con la teoría física del péndulo, que como se sabe, establece que el período de un péndulo es proporcional a la raíz cuadrada de su longitud, siendo la constante de proporcionalidad 2π /√g donde g es la aceleración de gravedad.
Este tipo de ajuste potencial no solo tiene el coeficiente de determinación más alto, sino que el exponente y la constante de proporcionalidad coinciden con el modelo físico.
-El ajuste por regresión determina los parámetros de la función que pretende explicar los datos mediante el método de mínimos cuadrados. Dicho método consiste en minimizar la sumatoria de la diferencia cuadrática entre el valor Y de ajuste y el valor Yi de los datos para los valores Xi de los datos. De esta forma se determinan los parámetros de la función de ajuste.
-Como hemos visto, la función de ajuste más común es la recta, pero no es la única, ya que los ajustes pueden ser también polinómicos, potenciales, exponenciales, logaritmos y otros.
-En todo caso, el coeficiente de determinación depende de los datos y del tipo de ajuste y es un indicativo de la bondad del ajuste aplicado.
-Por último, el coeficiente de determinación indica el porcentaje de variabilidad total entre el valor Y de los datos respecto al valor Ŷ del ajuste para los X dados.
- González C. Estadística General. Recuperado de: tarwi.lamolina.edu.pe
- IACS. Instituto Aragonés de Ciencias de Salud. Recuperado de: ics-aragon.com
- Salazar C. y Castillo S. Principios básicos de estadística. (2018). Recuperado de: dspace.uce.edu.ec
- Superprof. Coeficiente de determinación. Recuperado de: superprof.es
- USAC. Manual de estadística descriptiva. (2011). Recuperado de: estadistica.ingenieria.usac.edu.gt.
- Wikipedia. Coeficiente de determinación. Recuperado de: es.wikipedia.com.
