Ángulo inscrito de una circunferencia: definición, teoremas, ejemplos
El ángulo inscrito de una circunferencia es aquel que tiene su vértice sobre la circunferencia y sus semirrectas son secantes o tangentes a la misma. Como consecuencia el ángulo inscrito siempre será convexo o plano.
En la figura 1 se representan varios ángulos inscritos en sus respectivas circunferencias. El ángulo ∠EDF es inscrito por tener su vértice D sobre la circunferencia y sus dos semirrectas [DE) y [DF) secantes a la circunferencia.
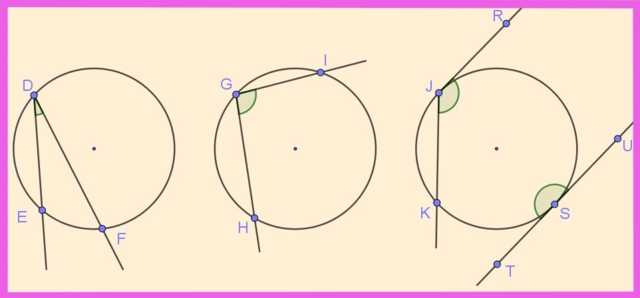
De forma semejante, el ángulo ∠HGI es inscrito, por tener su vértice en la circunferencia y sus lados secantes a la misma.
Los ángulos ∠KJR y ∠UST también son inscritos a la circunferencia. El primero de ellos tiene un lado secante y el otro tangente, mientras que el segundo tiene sus dos lados tangentes a la circunferencia, formando un ángulo inscrito plano (180º).
Algunos autores llaman ángulo semi-inscrito al que tiene uno de sus lados tangente a la circunferencia, pero en este artículo se le considera inscrito.
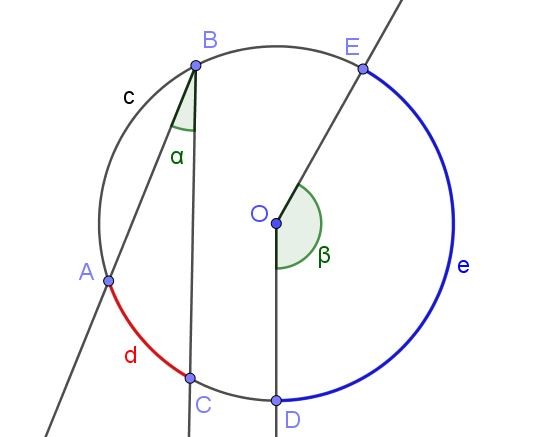
Todo ángulo inscrito define o subtiende un arco asociado a la misma. Por ejemplo en la figura 2 el ángulo inscrito ∠ABC subtiende el arco A⌒C de longitud d.
En la misma figura se muestra el ángulo ∠DOE, que no es inscrito en la circunferencia por no tener su vértice sobre su circunferencia, sino en el centro O.
Índice del artículo
Además del ángulo inscrito, en una circunferencia puede definirse el ángulo central, que es aquel cuyo vértice está en el centro de la circunferencia y cuyos lados cortan a la circunferencia.
La medida en radianes de un ángulo central es el cociente entre el arco que subtiende, es decir el arco de circunferencia comprendido entre los lados del ángulo, y el radio de la circunferencia.
Si la circunferencia es unitaria (de radio 1), entonces la longitud del arco en la mismas unidades de radio es la medida del ángulo en radianes.
Y cuando se requiere la medida del ángulo en grados, entonces se multiplica la medida en radianes por el factor 180º/π.
Los instrumentos de medición de ángulos siempre usan un ángulo central y la longitud del arco subtendido por esta directamente calibrada en grados. Esto significa que siempre que se mide un ángulo, en el fondo lo que se mide es la longitud del arco subtendido por el ángulo central.
La medida de un ángulo inscrito es la mitad de la medida del ángulo central, si ambos ángulos subtienden el mismo arco.
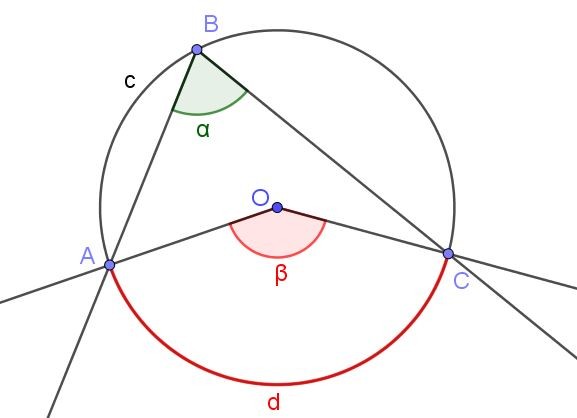
En la figura 4 se muestran dos ángulos ∠ABC y ∠AOC, que intersectan el mismo arco de circunferencia A⌒C.
Si la medida del ángulo inscrito es α, entonces la medida β del ángulo central es el doble de la medida del ángulo inscrito (β = 2 α) debido a que ambos subtienden el mismo arco de medida d.
Demostración 1a
Para demostrar el teorema 1, se comenzará mostrando varios casos particulares, hasta llegar al caso general.
Supongamos un ángulo inscrito, en el que uno de sus lados pasa por el centro de la circunferencia, tal como lo muestra la figura 5.
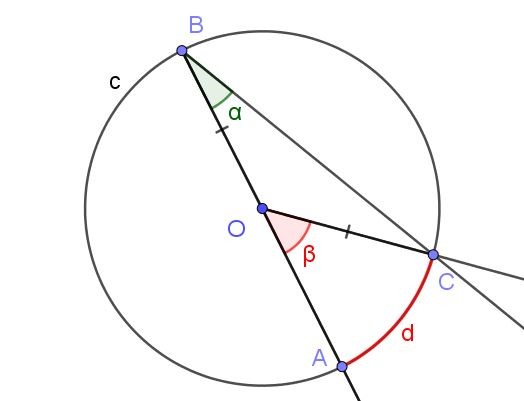
En este caso, se forma el triángulo isósceles COB, ya que [OC] = [OB].
En un triángulo isósceles, los ángulos adyacentes a la base son iguales, por lo tanto se tienen que ∠BCO = ∠ABC = α. Por otra parte ∠COB = 180º – β.
Considerando la suma de los ángulos internos del triángulo COB se tiene:
α + α + (180º – β) = 180º
De donde se deduce que 2 α = β, o lo que es equivalente: α = β/2. Esto coincide con lo que afirma el teorema 1: la medida del ángulo inscrito es la mitad del ángulo central, si ambos ángulos subtienden la misma cuerda [AC].
Demostración 1b
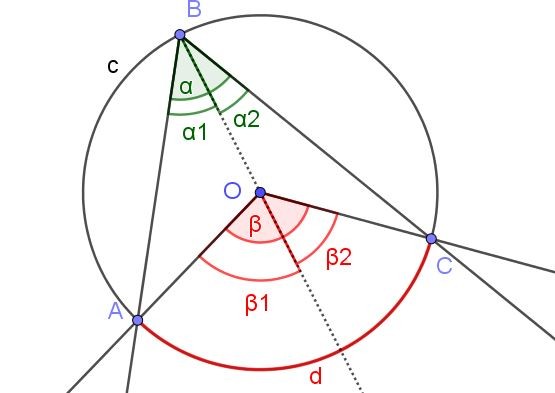
En este caso se tiene un ángulo inscrito ∠ABC, en el que el centro O de la circunferencia está dentro del ángulo.
Para demostrar el teorema 1 en este caso, se traza la semirrecta auxiliar [BO), de modo que se tienen dos ángulos inscritos ∠ABO y ∠OBC adyacentes a dicha semirrecta.
Similarmente se tienen los ángulos centrales β1 y β2 adyacentes a dicha semirrecta. De esta manera se tiene la misma situación que en demostración 1a, por lo que puede afirmarse que α2 = β2 /2 y α1 = β1 /2. Como α = α1 + α2 y β = β1 + β2 se tiene por tanto que α = α1 + α2 = β1 /2 + β2 /2 = (β1 + β2) / 2 = β / 2.
En conclusión α = β / 2, lo cual cumple el teorema 1.
Si dos o más ángulos inscritos subtienden el mismo arco, entonces tienen la misma medida.
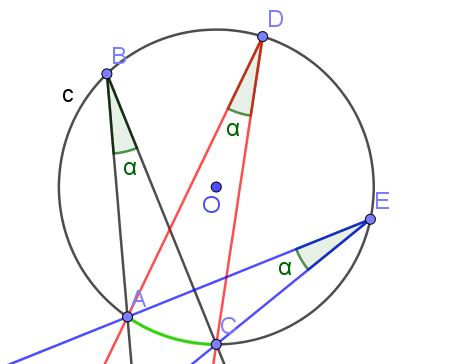
Los ángulos inscritos que subtienden cuerdas de la misma medida son iguales.
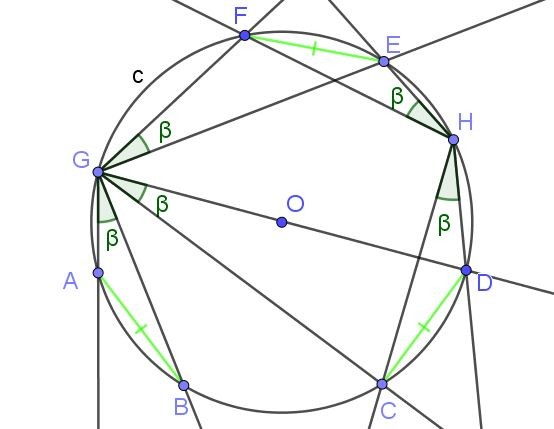
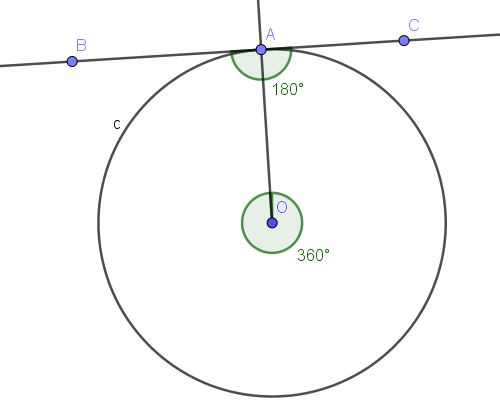
Demostrar que el ángulo inscrito que subtiende el diámetro es un ángulo recto.
Solución
El ángulo central ∠AOB asociado al diámetro es un ángulo plano, cuya medida es 180º.
De acuerdo al teorema 1, todo ángulo inscrito en la circunferencia que subtiende la misma cuerda (en este caso el diámetro), tiene como medida la mitad del ángulo central que subtiende la misma cuerda, que para nuestro ejemplo es 180º/2 = 90º.
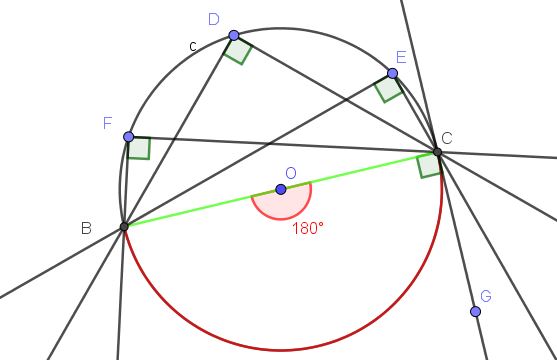
La recta (BC) tangente en A a la circunferencia C, determina el ángulo inscrito ∠BAC (ver figura 10).
Verificar que se cumple el teorema 1 de los ángulos inscritos.
Solución
El ángulo ∠BAC es inscrito porque su vértice está sobre la circunferencia, y sus lados [AB) y [AC) son tangentes a la circunferencia, por lo que se cumple la definición de ángulo inscrito.
Por otra parte, el ángulo inscrito ∠BAC subtiende el arco A⌒A, el cual es la circunferencia completa. El ángulo central que subtiende el arco A⌒A es un ángulo convexo cuya medida es el ángulo completo (360º).
El ángulo inscrito que subtiende el arco completo mide la mitad del ángulo central asociado, es decir ∠BAC = 360º/2 = 180º.
Con todo lo anterior se comprueba que este caso particular cumple el teorema 1.
- Baldor. (1973). Geometría y trigonometría. Editorial cultural centroamericana.
- E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad de Medellín.
- Geometría 1ro ESO. Ángulos en la circunferencia. Recuperado de: edu.xunta.es/
- Todo Ciencia. Ejercicios propuestos de ángulos en la circunferencia. Recuperado de: francesphysics.blogspot.com
- Wikipedia. Ángulo inscrito. Recuperado de: es.wikipedia.com
