Suma de Riemann: historia, fórmulas y propiedades, ejercicios
La suma de Riemann es el nombre que recibe el cálculo aproximado de una integral definida, mediante una sumatoria discreta con un número de términos finito. Una aplicación común es la aproximación del área de funciones en un gráfico.
Fue el matemático alemán Georg Friedrich Bernhard Riemann (1826-1866) quien ofreció por primera vez una definición rigurosa de la integral de una función en un intervalo dado. La dio a conocer en un artículo publicado en 1854.

La suma de Riemann se define sobre una función y = f(x), con x perteneciente al intervalo cerrado [a, b]. Sobre este intervalo se efectúa una partición P de n elementos:
P = {x0= a, x1, x2, …, xn= b}
Esto significa que el intervalo se divide de la siguiente manera:
xk-1 ≤ tk ≤ xk
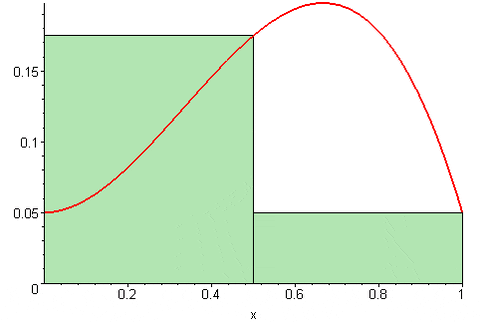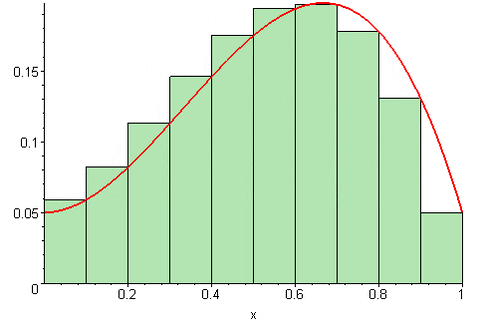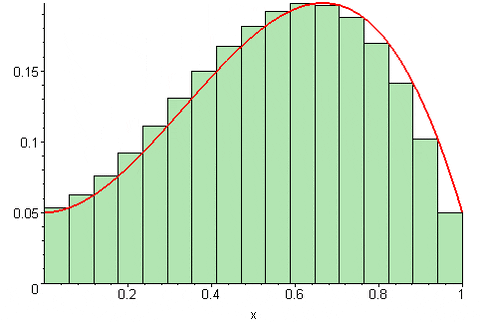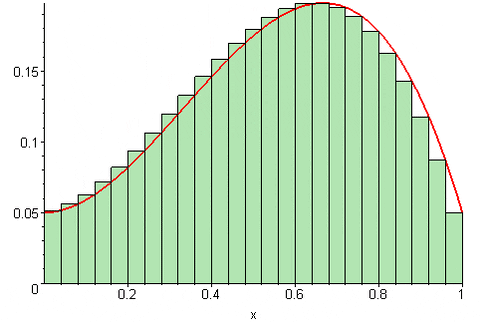
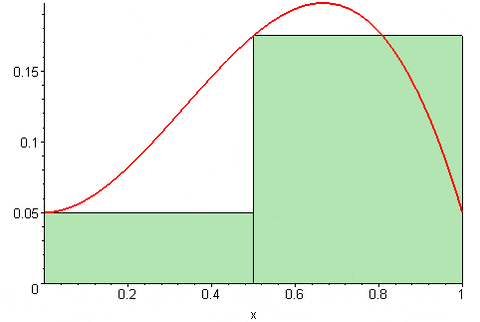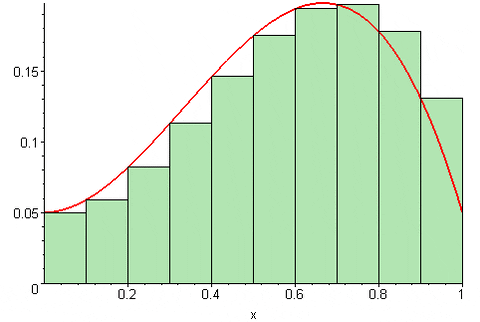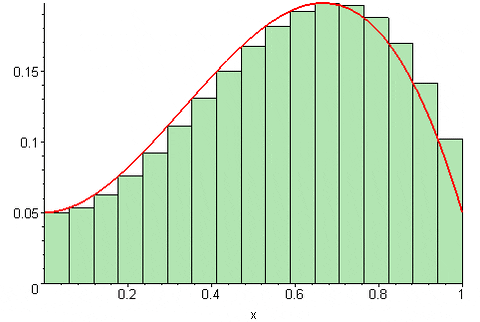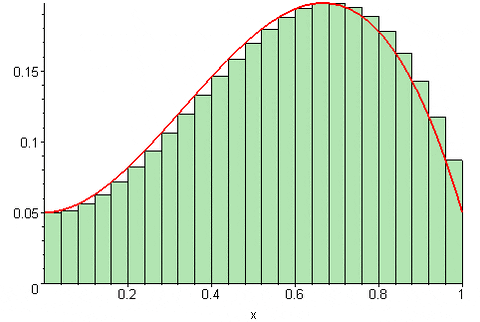
En la figura 1 se muestra gráficamente la suma de Riemann de la función f en el intervalo [x0, x4] sobre una partición de cuatro subintervalos, los rectángulos de color gris.
La suma representa el área total de los rectángulos y el resultado de esta suma se aproxima numéricamente al área bajo la curva f, entre las abscisas x=x0 y x=x4.
Desde luego, la aproximación al área bajo la curva mejora muchísimo en la medida que el número n de particiones sea mayor. De esta manera la suma converge al área bajo la curva, cuando el número n de particiones tiende a infinito.
Índice del artículo
La suma de Riemann de la función f(x) sobre la partición:
P = {x0= a, x1, x2, …, xn= b}
Definida sobre el intervalo [a, b], está dada por:
S(P, f) = ∑k=1n f(tk) (xk – xk-1)
Donde tk es un valor en el intervalo [xk, xk-1]. En la suma de Riemann se suelen usar intervalos regulares de ancho Δx = (b – a)/n, donde a y b son los valores mínimo y máximo de la abscisa, mientras que n es el número de subdivisiones.
En ese caso la suma derecha de Riemann es:
Sd(f, n)= [f(a+Δx) +f(a+2Δx)+ …+f(a+(n-1)Δx)+f(b)]*Δx
Mientras que la suma izquierda de Riemann se expresa como:
Si(f, n)= [f(a) +f(a+Δx)+ …+f(a+(n-1)Δx)]*Δx
Por último la suma central de Riemann es:
Sc(f, n)= [f(a+ Δx/2) +f(a+ 3Δx/2)+ …+f(b- Δx/2 )]*Δx
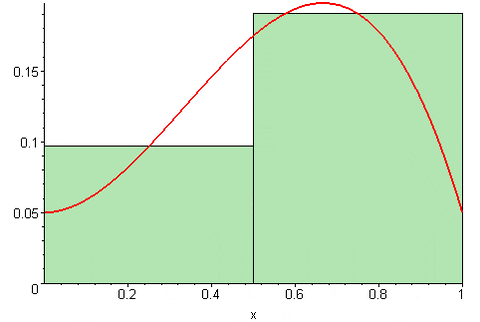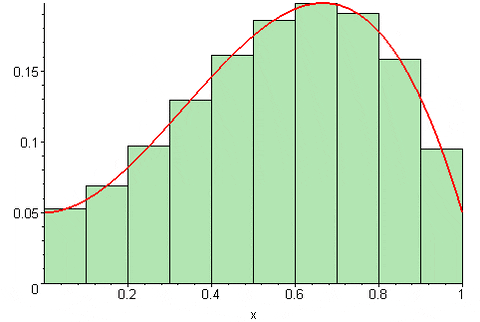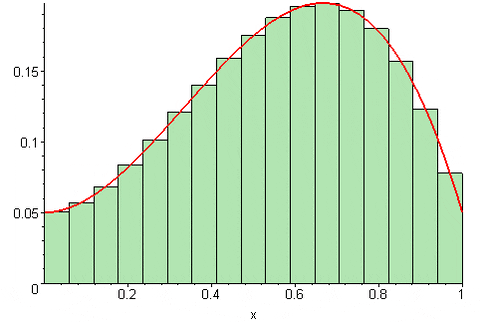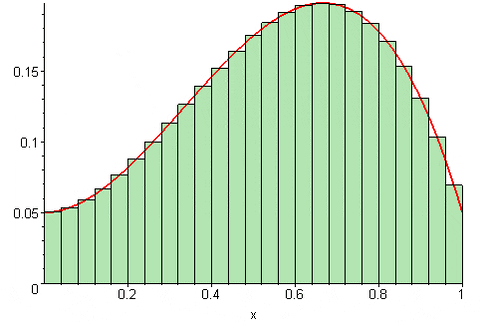
Dependiendo de donde se sitúe el punto tk en el intervalo [xk, xk-1] la suma de Riemann puede sobreestimar o subestimar el valor exacto del área bajo la curva de la función y = f(x). Es decir, los rectángulos pueden sobresalir de la curva o bien quedar un poco por debajo de esta.
La principal propiedad de la suma de Riemann y de la cual deviene su importancia, es que si el número de subdivisiones tiende a infinito, el resultado de la suma converge a la integral definida de la función:
Calcular el valor de la integral definida entre a = -2 hasta b = +2 de la función:
f(x) = x2
Haga uso de una suma de Riemann. Para ello encuentre primero la suma para n particiones regulares del intervalo [a, b] y luego tome el límite matemático para el caso que el número de particiones tienda a infinito.
Solución
Estos son los pasos a seguir:
-En primer lugar se define el intervalo de las particiones como:
Δx = (b – a)/n.
-Luego la suma de Riemann por la derecha correspondiente a la función f(x) queda así:
[-2 +(4i/n)]2 = 4 – (16 i /n) + (4/n)2 i2
-Y luego se sustituye cuidadosamente en la sumatoria:
-El siguiente paso es separar las sumatorias y sacar las cantidades constantes como factor común de cada suma. Es preciso tomar en cuenta que el índice es i, por lo tanto los números y los términos con n son considerados constantes:
-Se evalúa cada sumatoria, ya que para cada una de ellas hay expresiones apropiadas. Por ejemplo, la primera de las sumatorias da n:
S(f, n) = 16 – 64(n+1)/2n + 64(n+1)(2n+1)/6n2
-Por último se tiene que la integral que se quiere calcular es:
= 16 -(64/2) + (64/3) = 16/3 = 5,333
El lector puede comprobar que este es el resultado exacto, el cual puede obtenerse resolviendo la integral indefinida y evaluando los límites de integración por la regla de Barrow.
Determine en forma aproximada el área bajo la función:
f(x) = (1/√(2π)) e(-x2/2)
Entre x=-1 y x=+1, usando una suma central de Riemann con 10 particiones. Comparar con el resultado exacto y estimar la diferencia porcentual.
Solución
El paso o incremento entre dos valores discretos sucesivos es:
Δx = (1 – (-1)/10 = 0,2
De modo que la partición P sobre la que se definen los rectángulos queda así:
P = {-1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1,0}
Pero como lo que se quiere es la suma central, la función f(x) será evaluada en los puntos medios de los subintervalos, es decir en el conjunto:
T = {-0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9}.
La suma (central) de Riemann queda así:
S=f(-0,9)*0,2 + f(-0,7)*0,2+f(-0,5)*0,2+…+f(0,7)*0,2+f(0,9)*0,2
Dado que la función f es simétrica, es posible reducir la suma a solo 5 términos y el resultado se multiplica por dos:
S = 2*0,2*{f(0,1)+ f(0,3)+ f(0,5)+ f(0,7)+ f(0,9)}
S = 2*0,2*{0,397+ 0,381+ 0,352+ 0,312+ 0,266}=0,683
La función dada en este ejemplo no es otra que la conocida campana de Gauss (normalizada, con media igual a cero y desviación estándar uno). Se sabe que el área bajo la curva en el intervalo [-1,1] para esta función es 0,6827.

Esto significa que la solución aproximada con apenas 10 términos coincide con la solución exacta hasta tres decimales. El error porcentual entre la integral aproximada y la exacta es de 0,07%.
- Casteleiro, J. M., & Gómez-Álvarez, R. P. (2002). Cálculo integral (Illustrated ed.). Madrid: ESIC Editorial.
- Unican. Historia del concepto de integral. Recuperado de: repositorio.unican.es
- UIS. Sumas de Riemann. Recuperado de: matematicas.uis.edu.co
- Wikipedia. Suma de Riemann. Recuperado de: es.wikipedia.com
- Wikipedia. Integración de Riemann. Recuperado de: es.wikipedia.com
