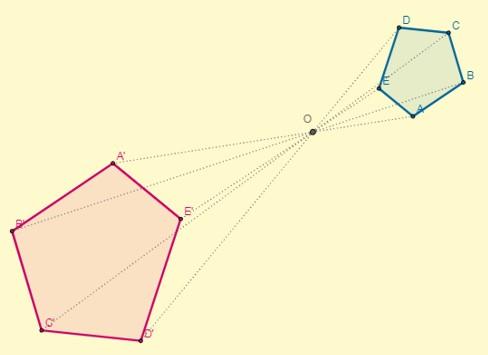
Homotecia: concepto, fórmula, propiedades, tipos, ejemplos

La homotecia es un cambio geométrico en el plano donde, a partir de un punto fijo llamado centro (O), se multiplican las distancias por un factor común. De esta forma, cada punto P corresponde a otro punto P’ producto de la transformación, y estos se encuentran alineados con el punto O.

Entonces, la homotecia se trata de una correspondencia entre dos figuras geométricas, donde los puntos transformados son llamados homotéticos, y estos se encuentran alineados con un punto fijo y con segmentos paralelos entre sí.

Explicación y fórmula

La homotecia es una transformación que no tiene una imagen congruente, porque a partir de una figura se van a obtener una o más figuras de mayor o menor tamaño que la figura original; es decir, que la homotecia transforma un polígono en otro semejante.

Para que la homotecia se cumpla deben corresponder punto a punto y recta a recta, de forma que las parejas de puntos homólogos estén alineadas con un tercer punto fijo, que es el centro de la homotecia.

Así mismo, las parejas de rectas que los unen deben ser paralelas. La relación entre tales segmentos es una constante llamada razón de la homotecia (k); de tal forma que la homotecia puede ser definida como:

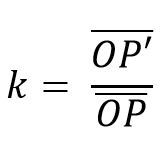
Para hacer este tipo de transformación se comienza escogiendo un punto arbitrario, que será el centro de la homotecia.

A partir de este punto se trazan segmentos de recta para cada vértice de la figura que se va a transformar. La escala en la que se hace la reproducción de la nueva figura es dada por la razón de la homotecia (k).

Propiedades de la homotecia

Una de las principales propiedades de la homotecia es que, por la razón de la homotecia (k), todas las figuras homotéticas son semejantes. Entre otras propiedades destacadas se encuentran las siguientes:

– El centro de la homotecia (O) es el único punto doble y este se transforma en sí mismo; es decir, no varía.

– Las rectas que pasan por el centro se transforman en sí mismas (son dobles), pero los puntos que la componen no son dobles.

– Las rectas que no pasan por el centro se transforman en rectas paralelas; de esa forma, los ángulos de la homotecia se mantienen iguales.

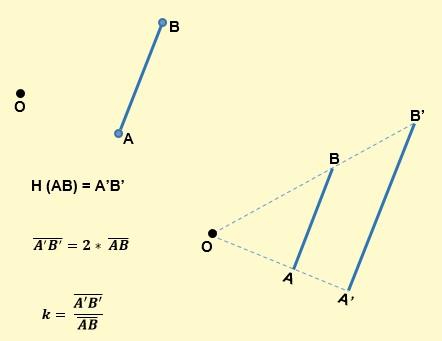
– La imagen de un segmento por una homotecia de centro O y razón k, es un segmento paralelo a este y tiene k veces su longitud. Por ejemplo, como se observa en la siguiente imagen, un segmento AB por homotecia resultará otro segmento A’B’, de tal forma que AB será paralelo a A’B’ y la k será:

– Los ángulos homotéticos son congruentes; es decir, tienen la misma medida. Por lo tanto, la imagen de un ángulo es un ángulo que tiene su misma amplitud.

Por otra parte, se tiene que la homotecia varía en función del valor de su razón (k), y pueden ocurrir los siguientes casos:

– Si la constante k = 1, todos los puntos son fijos porque se transforman a sí mismos. Así, la figura homotética coincide con la original y la transformación se llamará función identidad.

– Si k ≠ 1, el único punto fijo será el centro de la homotecia (O).

– Si k = -1, la homotecia se convierte en una simetría central (C); es decir, ocurrirá una rotación alrededor de C, en un ángulo de 180^o.

– Si k > 1, el tamaño de la figura transformada será mayor al tamaño de la original.

– Si 0 k 1, el tamaño de la figura transformada será menor que el de la original.

– Si -1 k 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

– Si k -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Tipos de homotecia

La homotecia también pude ser clasificada en dos tipos, en función del valor de su razón (k):

Homotecia directa

Ocurre si la constante k > 0; es decir, los puntos homotéticos se encuentran al mismo lado con respecto al centro:

El factor de proporcionalidad o razón de semejanza entre las figuras homotéticas directas siempre será positivo.

Homotecia inversa

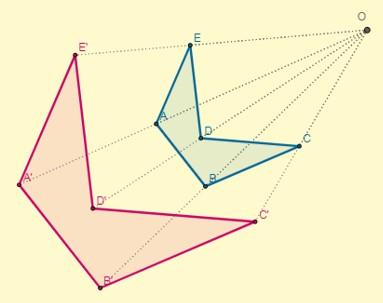
Ocurre si la constante k 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

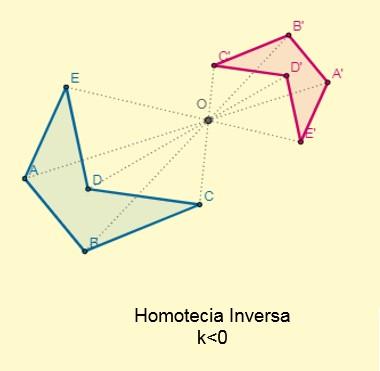
El factor de proporcionalidad o razón de semejanza entre las figuras homotéticas inversas siempre será negativo.

Composición

Cuando se realizan sucesivamente varios movimientos hasta obtener una figura igual a la original, ocurre una composición de movimientos. La composición de varios movimientos es también un movimiento.

La composición entre dos homotecias tiene como resultado una nueva homotecia; es decir, se tiene un producto de homotecias en el que el centro estará alineado con el centro de las dos transformaciones originales, y la razón (k) es el producto de las dos razones.

Así, en la composición de dos homotecias H₁(O₁, k₁) y H₂(O₂, k₂), la multiplicación de sus razones: k₁ x k₂ = 1 tendrá como resultado una homotecia de razón k₃ =  k₁ x k₂. El centro de esta nueva homotecia (O₃) estará ubicado sobre la recta O₁ O₂.

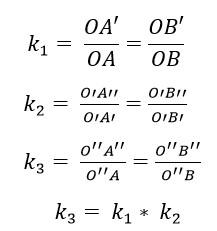
La homotecia corresponde a un cambio plano e irreversible; si se aplican dos homotecias que posean igual centro y razón pero con diferente signo, se obtendrá la figura original.

Ejemplos de homotecia

1. Primer ejemplo

Aplicar una homotecia al polígono dado de centro (O), ubicado a 5 cm del punto A y cuya razón es k = 0,7.

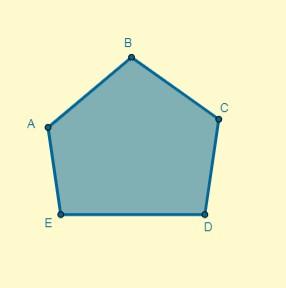
Solución

Se escoge un punto cualquiera como centro de la homotecia, y desde este se trazan semirrectas por los vértices de la figura:

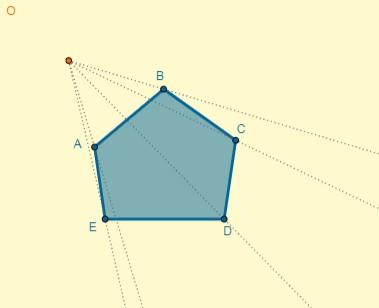
Se tiene que la distancia desde centro (O) hasta el punto A es OA = 5; con esta se puede determinar la distancia de uno de los puntos homotéticos (OA’) sabiendo también que k = 0,7:

OA’= k x OA.

OA’= 0,7 x 5 = 3,5.

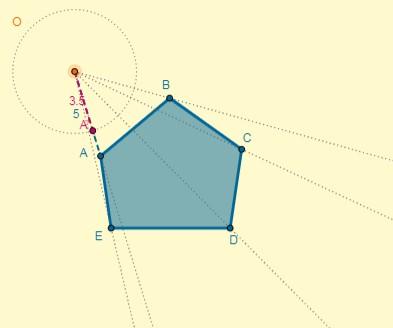
El proceso puede hacerse para cada vértice, o también se puede trazar el polígono homotético recordando que los dos polígonos tienen lados paralelos:

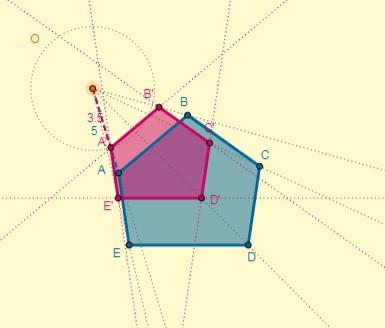
Finalmente, la transformación se ve de la siguiente forma:

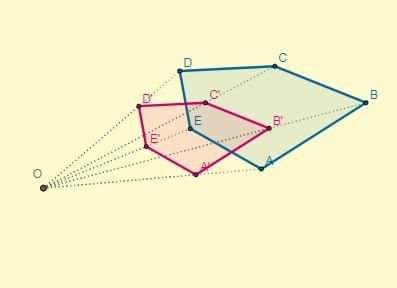
2. Segundo ejemplo

Aplicar una homotecia al polígono dado de centro (O), ubicado a 8,5 cm del punto C y cuya y razón k = -2.

Solución

Se tiene que la distancia desde centro (O) hasta el punto C es OC = 8,5; con este dato es posible determinar la distancia de uno de los puntos homotéticos (OC’), sabiendo también que k = -2:

OC’= k x OC.

OC’= -2 x 8,5 = -17

Después de trazar los segmentos de los vértices del polígono transformado, se tiene que los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro: