Ángulo nulo: definición y características, ejemplos, ejercicios
El ángulo nulo es aquel cuya medida vale 0, tanto en grados como en radianes u otro sistema de medida de ángulos. Por lo tanto carece de amplitud o de abertura, como el que se forma entre dos rectas paralelas.
Aunque su definición suena bastante simple, el ángulo nulo es muy útil en muchas aplicaciones de física e ingeniería, así como en navegación y diseño.
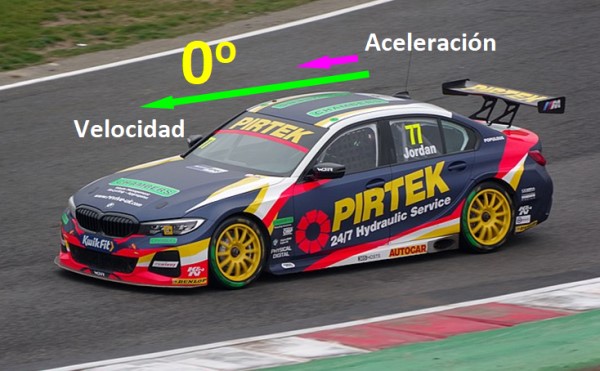
Hay cantidades físicas que deben alinearse paralelamente para lograr ciertos efectos: si un auto se mueve en línea recta por una autopista y entre su vector velocidad v y su vector aceleración a hay 0º, el auto cada vez se mueve más rápido, pero si el auto frena, su aceleración es opuesta a su velocidad (ver figura 1).
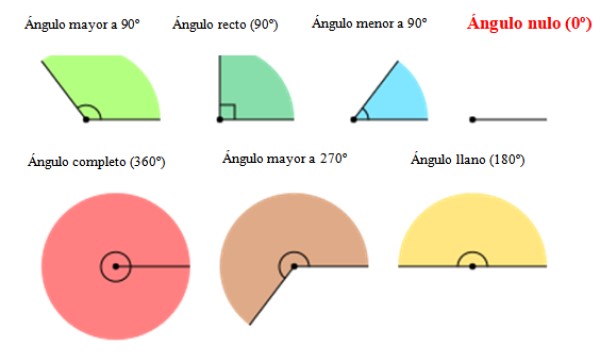
En la siguiente figura aparecen distintos tipos de ángulo incluyendo al ángulo nulo a la derecha. Como se puede apreciar, el ángulo 0º carece de amplitud o abertura.
Índice del artículo
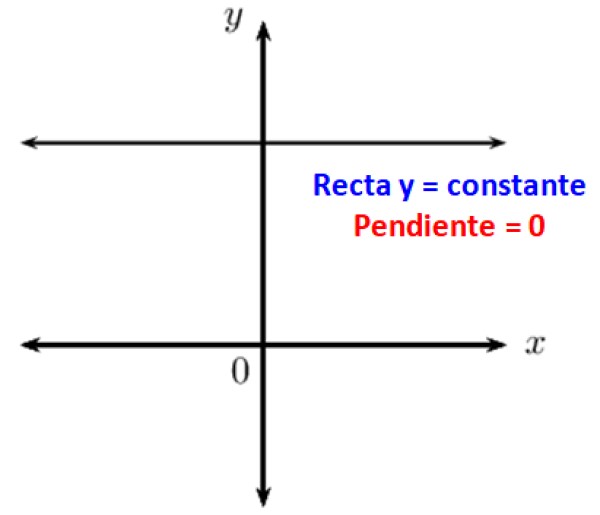
Se sabe que las rectas paralelas forman entre sí un ángulo nulo. Cuando se tiene una recta horizontal, esta es paralela al eje x del sistema de coordenadas cartesiano, por lo tanto su inclinación respecto a él es 0. En otras palabras, las rectas horizontales tienen pendiente nula.
Asimismo las razones trigonométricas del ángulo nulo son 0, 1 o infinito. Por lo tanto el ángulo nulo se hace presente en muchas situaciones físicas que involucran operaciones con vectores. Estas razones son:
-sen 0º = 0
-cos 0º = 1
-tg 0º = 0
-sec 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
Y serán de utilidad para analizar algunos ejemplos de situaciones en que la presencia del ángulo nulo desempeña un papel fundamental:
Suma de vectores
Cuando dos vectores son paralelos, el ángulo entre ellos es nulo, como se ve en la figura 4a de arriba. En tal caso, la suma de ambos se lleva a cabo colocando uno a continuación del otro y la magnitud del vector suma es la suma de las magnitudes de los sumandos (figura 4b).

Cuando dos vectores son paralelos, el ángulo entre ellos es nulo, como se ve en la figura 4a de arriba. En tal caso, la suma de ambos se lleva a cabo colocando uno a continuación del otro y la magnitud del vector suma es la suma de las magnitudes de los sumandos (figura 4b)
El torque o momento de torsión
El torque o momento de torsión origina la rotación de un cuerpo. Depende de la magnitud de la fuerza aplicada y de cómo esta se aplica. Un ejemplo muy representativo es la llave inglesa de la figura.
Para conseguir el mejor efecto de giro se aplica la fuerza perpendicularmente al mango de la llave, ya sea hacia arriba o hacia abajo, pero no se espera rotación si la fuerza es paralela al mango.
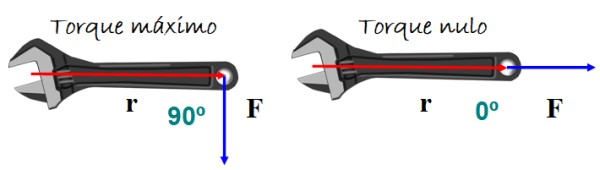
Matemáticamente el torque τ se define como el producto vectorial o producto cruz entre los vectores r (vector de posición) y F (vector fuerza) de la figura 5:
τ = r x F
La magnitud del torque es:
τ = r F sen θ
Siendo θ el ángulo entre r y F. Cuando sen θ = 0 el torque es nulo, en tal caso θ = 0º (o también 180º).
Flujo de campo eléctrico
El flujo de campo eléctrico es una magnitud escalar que depende de la intensidad del campo eléctrico así como de la orientación de la superficie por la que atraviesa.
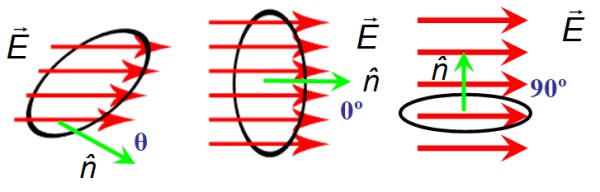
En la figura 6 hay una superficie circular de área A por la cual pasan las líneas del campo eléctrico E. La orientación de la superficie está dada por el vector normal n. A la izquierda el campo y el vector normal forman un ángulo agudo arbitrario θ, en el centro forman entre sí un ángulo nulo y la derecha están perpendiculares.
Cuando E y n son perpendiculares, las líneas de campo no atraviesan la superficie y por lo tanto el flujo es cero, mientras que cuando el ángulo entre E y n es nulo, las líneas atraviesan completamente la superficie.
Denotando el flujo de campo eléctrico mediante la letra griega Φ (se lee “fi”), su definición para un campo uniforme como en la figura, queda así:
Φ = E•nA
El punto en el medio de ambos vectores denota el producto punto o producto escalar, que alternativamente se define así:
Φ = E•nA = EAcosθ
Las negritas y las flechas encima de la letra son recursos para diferenciar entre un vector y su magnitud, que se denota con letras normales. Dado que cos 0 = 1, el flujo es máximo cuando E y n son paralelos.
Dos fuerzas P y Q actúan simultáneamente sobre un objeto puntual X, ambas fuerzas forman inicialmente un ángulo θ entre ellas. ¿Qué le sucede a la magnitud de la fuerza resultante cuando θ decrece hasta anularse?

Solución
La magnitud de la fuerza resultante Q + P va aumentando paulatinamente hasta ser máxima cuando Q y P están totalmente paralelas (figura 7 derecha).
Señale si el ángulo nulo es solución de la siguiente ecuación trigonométrica:
cos 2x = 1 + 4sen x
Solución
Una ecuación trigonométrica es aquella en la cual la incógnita forma parte del argumento de una razón trigonométrica. Para la resolver la ecuación propuesta, es conveniente hacer uso de la fórmula para el coseno del ángulo doble:
cos 2x = cos2 x – sen2 x
Porque de esta forma, el argumento en lado izquierdo pasa a ser x en vez de 2x. Entonces:
cos2 x – sen2 x = 1 + 4sen x
Por otro lado cos2 x + sen2 x = 1, así que:
cos2 x – sen2 x = cos2 x + sen2 x + 4sen x
El término cos2 x se cancela y queda:
– sen2 x = sen2 x + 4sen x → – 2sen2 x – 4senx = 0 → 2sen2 x + 4senx = 0
Ahora se hace el siguiente cambio de variable: senx = u y la ecuación se transforma en:
2u2 + 4u = 0
2u(u+4) = 0
Cuyas soluciones son: u = 0 y u = -4. Retornando el cambio tendríamos dos posibilidades: sen x = 0 y senx = -4. Esta última solución no es viable, porque el seno de cualquier ángulo está comprendido entre -1 y 1, por lo que nos quedamos con la primera alternativa:
sen x = 0
Por lo tanto x = 0º es una solución, pero también sirve cualquier ángulo cuyo seno sea 0, que puede ser también 180º (π radianes), 360º (2 π radianes ) y los respectivos negativos también.
La solución más general de la ecuación trigonométrica es: x = kπ donde k= 0, ± 1, ±2, ±3,…. k un número entero.
- Baldor, A. 2004. Geometría plana y del espacio con Trigonometría. Publicaciones Cultural S.A. de C.V. México.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 3. Sistemas de Partículas. Editado por Douglas Figueroa (USB).
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Interacción Eléctrica. Editado por Douglas Figueroa (USB).
- OnlineMathLearning. Types of angles. Recuperado de: onlinemathlearning.com.
- Zill, D. 2012. Álgebra, Trigonometría y Geometría Analítica. McGraw Hill Interamericana.
