Vector normal: cálculo y ejemplo
El vector normal es aquel que define la dirección perpendicular a alguna entidad geométrica bajo consideración, la cual puede ser por una curva, un plano o una superficie, por ejemplo.
Se trata de un concepto muy útil en el posicionamiento de una partícula móvil o alguna superficie en el espacio. En la siguiente gráfica es posible ver como es el vector normal a una curva arbitraria C:
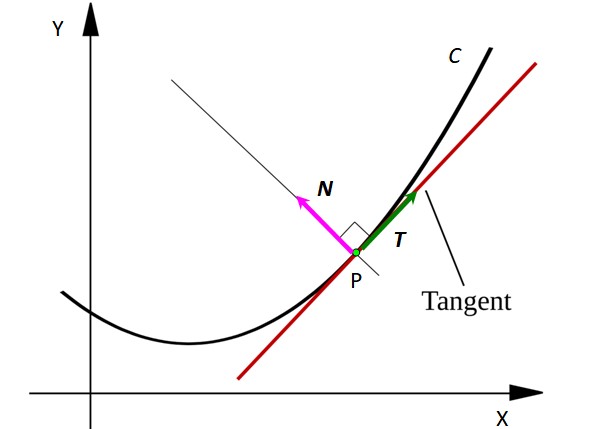
Considere un punto P sobre la curva C. El punto puede representar a una partícula móvil que se desplaza siguiendo una vía en forma de C. La recta tangente a la curva en el punto P aparece dibujada en color rojo.
Observe que el vector T es tangente a C en cada punto, mientras que el vector N es perpendicular a T y apunta al centro de una circunferencia imaginaria cuyo arco es un segmento de C. Los vectores se denotan en letra negrita en texto impreso, para distinguirlos de otras magnitudes no vectoriales.
El vector T siempre indica hacia dónde se mueve la partícula, por lo tanto señala la velocidad de la misma. En cambio el vector N apunta siempre en la dirección en la cual la partícula está girando, de esto modo señala la concavidad de la curva C.
Índice del artículo
El vector normal no necesariamente es un vector unitario, es decir, un vector cuyo módulo es 1, pero de ser así, se le llama vector unitario normal.
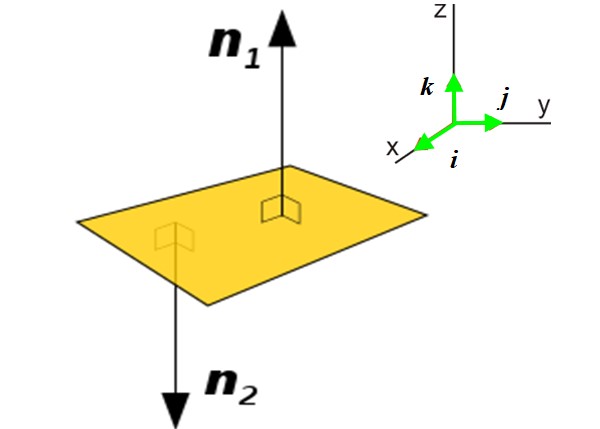
En numerosas aplicaciones es preciso conocer el vector normal a un plano en lugar de una curva. Este vector da a conocer la orientación de dicho plano en el espacio. Por ejemplo, consideremos el plano P (amarillo) de la figura:
Hay dos vectores normales a dicho plano: n1 y n2. El uso de uno u otro dependerá del contexto en que se encuentre dicho plano. Obtener el vector normal a un plano es muy sencillo si se conoce la ecuación del mismo:
ax + by + cz + d = 0, con a, b, c y d números reales.
Pues bien, un vector normal a dicho plano viene dado por:
N = a i + b j + c k
Aquí el vector N viene expresado en términos de los vectores unitarios y perpendiculares entre sí i, j y k, dirigidos a lo largo de la tres direcciones que determinan el espacio xyz, véase la figura 2 derecha.
Un procedimiento muy sencillo para encontrar el vector normal hace uso de las propiedades del producto vectorial entre dos vectores.
Como es sabido, tres puntos diferentes y no colineales entre sí, determinan un plano P. Ahora bien, es posible obtener dos vectores u y v que pertenezcan a dicho plano disponiendo de estos tres puntos.
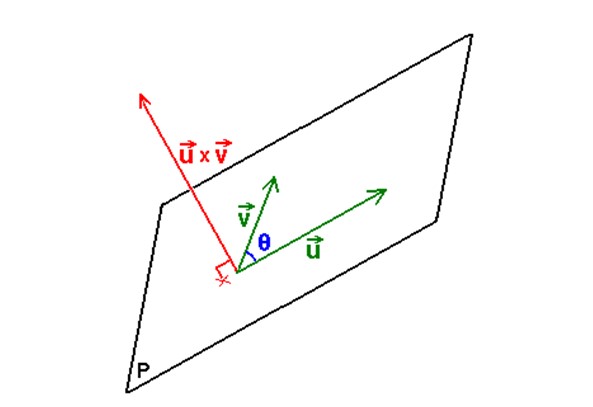
Una vez que se tengan los vectores, el producto vectorialu x v es una operación cuyo resultado es a su vez un vector, el cual tiene la propiedad de ser perpendicular al plano determinado por u y v.
Conocido este vector, se le denota como N, y a partir de él será posible determinar la ecuación del plano gracias a la ecuación indicada en la sección precedente:
N = u x v
En la siguiente figura se ilustra el procedimiento descrito:
Hallar la ecuación del plano determinado por los puntos A (2,1,3) ; B(0,1,1) ; C(4,2,1).
Este ejercicio ilustra el procedimiento anteriormente descrito. Al disponer de 3 puntos, se escoge uno de ellos como origen común de dos vectores que pertenezcan al plano definido por dichos puntos. Por ejemplo, se fija el punto A como origen y se construyen los vectores AB y AC.
El vector AB es el vector cuyo origen es el punto A y cuyo extremo es el punto B. Las coordenadas del vector AB se determinan restando respectivamente las coordenadas de B de las coordenadas de A:
AB = (0-2) i + (1-1) j + (1-3) k = -2i + 0j -2 k
Se procede del mismo modo para encontrar el vector AC:
AC = (4-2) i + (2-1) j + (1-3) k = 2i + j -2 k
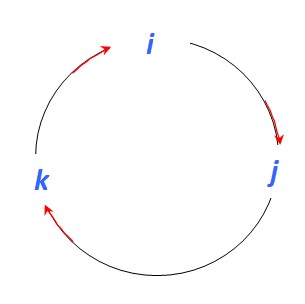
Existen varios procedimientos para encontrar el producto vectorial entres dos vectores. En este ejemplo se utiliza un procedimiento nemotécnico que hace uso de la siguiente figura para encontrar los productos vectoriales entre los vectores unitarios i, j y k:
Para comenzar es bueno recordar que los productos vectoriales entre vectores paralelos son nulos, por lo tanto:
i x i = 0; j x j = 0; k x k = 0
Y como el producto vectorial es otro vector perpendicular a los vectores participantes, al moverse en dirección a la flecha roja se tiene:
i x j = k ; j x k = i; k x i = j
Si hay que moverse en sentido contrario a la flecha entonces se agrega un signo (-):
j x i = – k; k x j = –i; i x k = –j
En total es posible hacer 9 productos vectoriales con los vectores unitarios i, j y k, de los cuales 3 serán nulos.
AB x AC = (-2i + 0j -2 k) x (2i + j -2 k)= -4(i x i) -2(i x j)+4 (i x k)+0 (j x i) + 0 (j x j) – 0 (j x k) – 4 (k x i)-2 (k x j) + 4 (k x k) = -2k-4j-4j+2i = 2i -8j-2k
Ecuación del plano
El vector N ha quedado determinado por el producto vectorial calculado previamente:
N = 2i -8j-2k
Por lo tanto a =2, b = -8, c = -2, el plano buscado es:
ax + by + cz + d = 0 → 2x-8y-2z +d = 0
Aún falta por determinar el valor de d. Esto es fácil si se sustituyen en la ecuación del plano los valores de cualquiera de los puntos A, B o C de los que se dispone. Eligiendo C por ejemplo:
x = 4; y = 2; z = 1
Queda:
2.4 – 8.2 – 2.1 + d = 0
-10 + d = 0
d = 10
En definitiva el plano buscado es:
2x-8y-2z +10 = 0
El lector inquisitivo puede preguntarse si se habría obtenido el mismo resultado si en vez de hacer AB x AC se hubiera elegido efectuar AC x AB. La respuesta es sí, el plano determinado por estos tres puntos es único y tiene dos vectores normales, como lo muestra la figura 2.
En cuanto al punto seleccionado como origen de los vectores, tampoco hay inconveniente en escoger cualquiera de los otros dos.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB). 31- 62.
- Finding the normal to a plane. Recuperado de: web.ma.utexas.edu.
- Larson, R. (1986). Cálculo y Geometría Analítica. Mc Graw Hill. 616 – 647.
- Lines and planes in R 3. Recuperado de: math.harvard.edu.
- Normal vector. Recuperado de mathworld.wolfram.com.
