Números irracionales: historia, propiedades, clasificación, ejemplos
Los números irracionales son aquellos cuya expresión decimal tiene infinitas cifras sin un patrón repetitivo, por lo tanto, no pueden obtenerse haciendo el cociente entre dos enteros cualesquiera.
Entre los números irracionales más conocidos están:

De entre ellos, sin lugar a dudas π (pi) es el más familiar, pero hay muchísimos más. Todos ellos pertenecen al conjunto de los números reales, que es el conjunto numérico que agrupa a los números racionales y a los irracionales.
Los puntos suspensivos en la figura 1 señalan que los decimales siguen indefinidamente, lo que pasa es que el espacio de las calculadoras corrientes solo permite mostrar unos cuantos.
Si nos fijamos cuidadosamente, siempre que hacemos el cociente entre dos números enteros, se obtiene un decimal con cifras limitadas o si no es así, con infinitas cifras en las que una o más se repiten. Pues bien, esto no sucede con los números irracionales.
Índice del artículo
- 1 Historia de los números irracionales
- 2 Propiedades de los números irracionales
- 3 Localización de un número irracional sobre la recta real
- 4 Clasificación de los números irracionales
- 5 Ejercicio
- 6 Referencias
El gran matemático de la antigüedad Pitágoras, nacido en 582 a.C en Samos, Grecia, fundó la escuela pitagórica del pensamiento y descubrió el famoso teorema que lleva su nombre. Lo tenemos acá abajo a la izquierda (puede que los babilonios ya lo conocieran desde mucho antes).
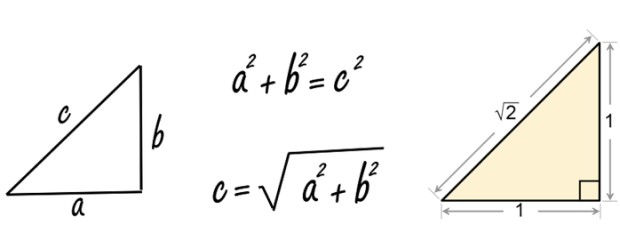
Pues bien, cuando Pitágoras (o probablemente un discípulo suyo) aplicó el teorema a un triángulo rectángulo de lados iguales a 1, encontró el número irracional √2.
Lo hizo de esta manera:
c = √12 + 12 = √1+1=√2
Y de inmediato se percató de que este nuevo número no provenía del cociente entre otros dos números naturales, que eran los que se conocían por aquel entonces.
Por lo tanto lo llamó irracional, y el descubrimiento causó gran zozobra y desconcierto entre los pitagóricos.
-El conjunto de todos los números irracionales se denota con la letra I y en ocasiones como Q* o QC. La unión entre los números irracionales I o Q* y los números racionales Q, da origen al conjunto de los números reales R.
-Con los números irracionales pueden realizarse las operaciones aritméticas conocidas: suma, resta, multiplicación, división, potenciación y más.
-La división entre 0 tampoco está definida entre los números irracionales.
-La suma y el producto entre números irracionales no necesariamente es otro número irracional. Por ejemplo:
√2 x √8 = √16 = 4
Y 4 no es un número irracional.
-Sin embargo, la suma de un número racional más uno irracional, sí da como resultado un irracional. De esta manera:
1 + √2 = 2.41421356237…
-El producto de un número racional diferente de 0 por un número irracional también es irracional. Veamos este ejemplo:
2 x √2= 2.828427125…
-El inverso de un irracional resulta en otro número irracional. Probemos con algunos:
1 / √2 = 0.707106781…
1 / √3 = 0.577350269…
Estos números son interesantes porque también son los valores de algunas razones trigonométricas de ángulos conocidos. Gran parte de las razones trigonométricas son números irracionales, pero hay excepciones, como por ejemplo sen 30º = 0.5 = ½, que es racional.
-En la suma se cumplen las propiedades conmutativa y asociativa. Si a y b son dos números irracionales, esto significa que:
a + b = b + a.
Y si c es otro número irracional, entonces:
(a+b) + c = a + (b+c).
-La propiedad distributiva de la multiplicación respecto a la suma es otra conocida propiedad que también se cumple para los números irracionales. En este caso:
a.(b+c) = a.b + a.c.
-Un irracional a tiene su opuesto: -a. Cuando se suman el resultado es 0:
a+(-a) = 0
-Entre dos racionales diferentes, hay al menos un número irracional.
La recta real es una línea horizontal donde se ubican los números reales, de los cuales los irracionales son una parte importante.
Para encontrar un número irracional sobre la recta real, en forma geométrica, podemos valernos del teorema de Pitágoras, una regla y un compás.
Como ejemplo vamos a ubicar a √5 sobre la recta real, para lo cual dibujamos un triángulo rectángulo de lados x = 2 y y = 1, como se muestra en la figura:
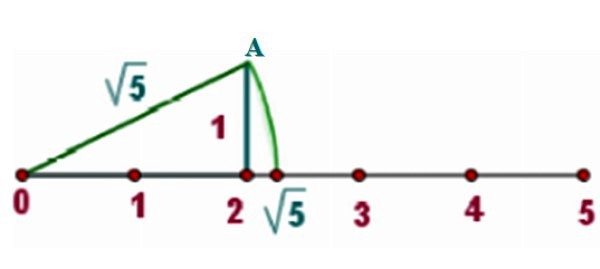
Por el teorema de Pitágoras, la hipotenusa de tal triángulo es:
c = √22 + 12 = √4+1=√5
Ahora se coloca el compás con la punta en 0, donde también está uno de los vértices del triángulo rectángulo. La punta del lápiz del compás debe estar en el vértice A.
Se traza un arco de circunferencia que corte a la recta real. Como la distancia entre el centro de la circunferencia y cualquier punto de la misma es el radio, el cual vale √5, el punto de intersección también dista √5 del centro.
De la gráfica se ve que √5 está comprendido entre 2 y 2.5. Una calculadora nos ofrece el valor aproximado de:
√5 = 2.236068
Y así, construyendo un triángulo con los lados apropiados, se pueden ubicar otros irracionales, como por ejemplo √7 y otros.
Los números irracionales se clasifican en dos grupos:
-Algebraicos
-Trascendentes o trascendentales
Los números algebraicos, que pueden ser irracionales o no, son soluciones de ecuaciones polinomiales cuya forma general es:
an xn + an-1xn-1 + an-2xn-2 + …. +a1x + ao = 0
Un ejemplo de ecuación polinomial es una ecuación de segundo grado como esta:
x3 – 2x = 0
Es fácil demostrar que el número irracional √2 es una de las soluciones de esta ecuación.
En cambio, los números trascendentes, aunque son irracionales, nunca surgen como solución de una ecuación polinomial.
Los números trascendentes encontrados con mayor frecuencia en las matemáticas aplicadas son π, por su relación con la circunferencia y el número e, o número de Euler, que es la base de los logaritmos neperianos.
Sobre un cuadrado negro se coloca uno gris en la posición señalada en la figura. Se sabe que la superficie del cuadrado negro es 64 cm2. ¿Cuánto valen las longitudes de ambos cuadrados?

La superficie de un cuadrado de lado L es:
A = L2
Como el cuadrado negro tiene 64 cm2 de área, su lado debe ser 8 cm.
Esta medida es la misma que la diagonal del cuadrado gris. Aplicando el teorema de Pitágoras a esta diagonal, y recordando que los lados de un cuadrado miden lo mismo, tendremos:
82 = Lg2 + Lg2
Donde Lg es el lado del cuadrado gris.
Por lo tanto: 2Lg2 = 82
Aplicando raíz cuadrada a ambos lados de la igualdad:
Lg = (8/√2) cm
- Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
- Figuera, J. 2000. Matemática 9no. Grado. ediciones CO-BO.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Portal Educativo. Los números irracionales y sus propiedades. Recuperado de: portaleducativo.net.
- Wikipedia. Números irracionales. Recuperado de: es.wikipedia.org.
