Número de coordinación: qué es, cálculo, ejemplos
El número de coordinación es la cantidad de átomos, iones o moléculas que interaccionan con un centro en los compuestos iónicos y de coordinación. Este concepto también puede aplicarse a las moléculas, teniendo en cuenta cuántos átomos se enlazan entre sí en lugar del número de sus enlaces.
Este número es importante porque define las geometrías de los complejos, las densidades de sus fases materiales, e inclusive el carácter estereoquímico (espacial) de sus reactividades. Para simplificar su definición, se consideran como vecino a todo átomo que rodea un centro en específico.

Considérese por ejemplo el piso compuesto de monedas de la imagen superior. Todas las monedas son del mismo tamaño, y si se observa cada una está rodeada de otras seis; es decir, tienen seis vecinos, y por lo tanto el número de coordinación (C.N.) para las monedas es de 6. Esta misma idea se extiende ahora al espacio tridimensional.
Si sus radios son desiguales, no todas tendrán el mismo número de coordinación. Por ejemplo: mientras más grande sea la moneda, más vecinos tendrá, pues podrá interactuar con un mayor número de monedas a su alrededor. Lo contrario sucede con las monedas pequeñas.
Índice del artículo
- 1 Concepto de número de coordinación
- 2 ¿Cómo se calcula o determina el número de coordinación?
- 3 Ejemplos de números de coordinación
- 4 Referencias
El número de coordinación es la cantidad de vecinos más cercanos y que, en principio, interaccionan directamente con un centro, el cual en su mayoría es un ion metálico. Así pues, dejamos a un lado las monedas para considerar esferas en su lugar.
Este ion metálico Mn+, donde n es igual a su número de oxidación o valencia, interacciona con otros vecinos (iónicos o moleculares) llamados ligandos. Cuanto mayor sea n (+2, +3, etc.), más pequeño será Mn+ y, en consecuencia, los ligandos se verán obligados a aproximarse más entre sí para interaccionar con Mn+.
La siguiente imagen ilustra lo anterior dicho:
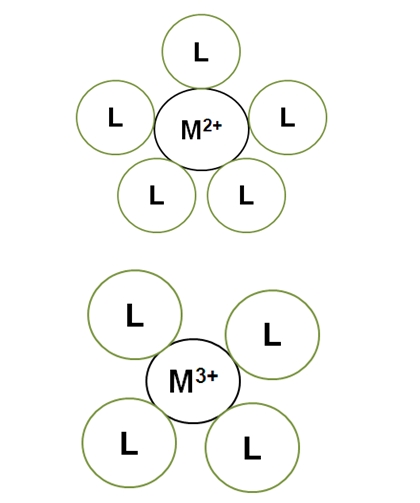
M2+ en el complejo ilustrado tiene un número de coordinación de 5: está rodeado de 5 ligandos L. Mientras, M3+ tiene un número de coordinación de 4. Esto se debe a que M3+, por tener una mayor magnitud de carga, su radio se contrae y, por lo tanto, los ligantes L deben acercarse más entre sí, lo cual incrementa sus repulsiones electrónicas.
Es por eso que los iones centrales voluminosos, como los pertenecientes a los metales del bloque f, o al segundo o tercer período del bloque d, tienden a tener números de coordinación más altos (C.N. > 6).
Supongamos ahora que el complejo de M3+ se somete a mucha presión. Llegará un punto en el que la presión será tal, que es probable que otro ligando se coordine o interaccione con M3+. Es decir, su número de coordinación aumentará de 4 a 5.
Por lo general, las presiones incrementan los números de coordinación, ya que se fuerzan a los vecinos a ceñirse sobre el ion o átomo central. En consecuencia, las fases materiales de estas sustancias se tornan más densas, más compactas.
Las ilustraciones superiores no dicen nada acerca de las geometrías entorno a M2+ o M3+. Sin embargo, sabemos que un cuadrado tiene cuatro vértices o esquinas, al igual que un tetraedro.
De este razonamiento se llega a la conclusión de que la geometría entorno a M3+, cuyo C.N. es 4, debe ser tetraédrica o cuadrada. Pero, ¿cuál de las dos? Mientras, las geometrías para M2+, cuyo C.N. es 5, pueden ser pirámide cuadrada o bipiramidal trigonal.
Cada C.N. tiene asociado varias posibles geometrías, las cuales posicionan los ligantes a una distancia favorable, de tal modo que haya la menor repulsión entre ellos.
El número de coordinación puede calcularse, a veces, directamente desde la fórmula del compuesto en cuestión. Supóngase el complejo aniónico [Ni(CN)5]3-. ¿Cuál es el número de coordinación para el ion níquel, Ni2+? Basta con observar el coeficiente estequiométrico 5, el cual indica que hay 5 aniones CN– coordinados o interaccionando con el centro de Ni2+.
No obstante, no siempre es así de fácil. Por ejemplo, el compuesto CuCN pareciera tener un número de coordinación de 1 tanto para el Cu2+ como para el CN–. Sin embargo, consiste en realidad de cadenas poliméricas Cu-CN-Cu-CN, por lo que el número de coordinación correcto es 2.
Es por eso que el número de coordinación es preferible determinarlo en lugar de calcularlo. ¿Cómo? Determinando las estructuras iónicas o moleculares de los compuestos. Esto es posible gracias a técnicas instrumentales como difracción de rayos X, de neutrones o de electrones.
A continuación y para finalizar se mencionarán algunos ejemplos de compuestos para cada uno de los números de coordinación más comunes. Asimismo, se dirán cuáles son sus respectivas geometrías.
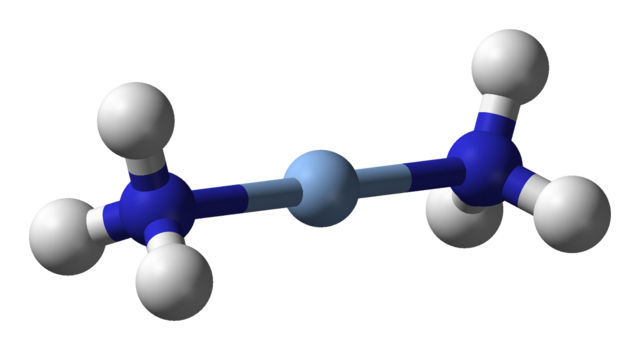
Un C.N. igual a 2 significa que el átomo o ion central solo tiene dos vecinos. Por lo tanto, hablamos de compuestos obligatoriamente de geometrías lineales. Entre ellos tenemos:
-Hg(CH3)2
-[Ag(NH3)2]+
-Ph3PAuCl

Un C.N. igual a 3 significa que el átomo o ion central está rodeado de tres vecinos. Tenemos entonces geometrías tales como: plano trigonal (triangular), pirámide trigonal y forma de T. Ejemplos de compuestos con este número de coordinación son:
-[Cu(CN)3]2-
-[Pt(PCy3)3], donde PCy se refiere al ligando triciclohexilofosfina
-Grafito
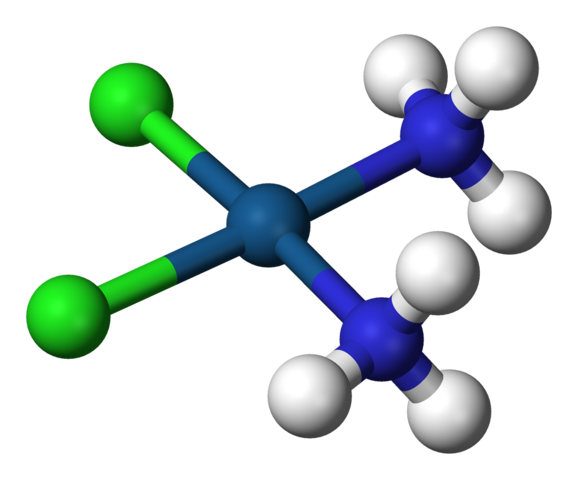
Un C.N. igual a 4 significa que el átomo o ion central está rodeado de cuatro vecinos. Sus geometrías posibles son la tetraédrica o la cuadrada. Ejemplos de compuestos con este número de coordinación tenemos los siguientes:
-CH4
-CoCl2pyr2
-cis-PtCl2(NH3)2
-[AlCl4]–
-[MoO4]2-
-SnCl4
-[CrO4]2-
-[MnO4]2-
Todos estos ejemplos, a excepción del cis-PtCl2(NH3)2, son de geometrías tetraédricas.
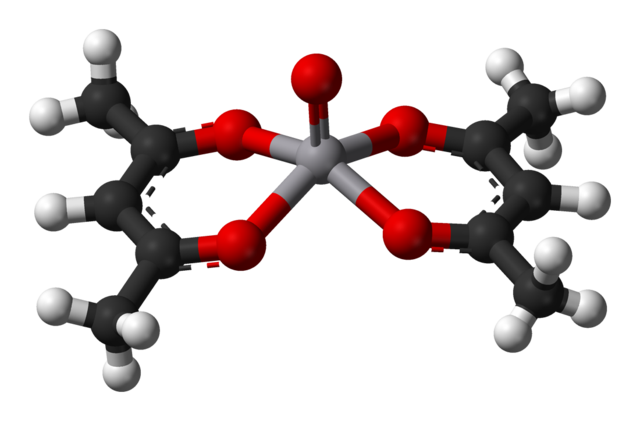
Un C.N. igual a 5 significa que el átomo o ion central se coordina o interacciona con cinco vecinos. Sus geometrías, ya mencionadas, son la pirámide cuadrada o la bipiramidal trigonal. Como ejemplos tenemos los siguientes:
-[CoBrN(CH2CH2NMe2)3]
-[Fe(CO)5]
-VO(acac)2, siendo acac el ligando acetilacetonato
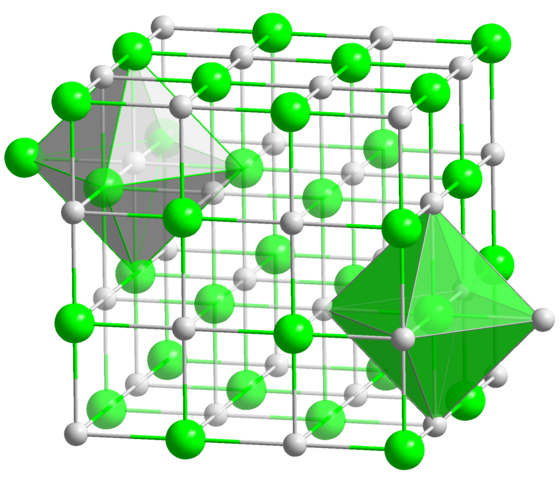
Este es, por lejos, el número de coordinación más común entre todos los compuestos. Recuérdese el ejemplo de las monedas del principio. Pero en lugar de que su geometría predilecta sea la de un hexágono plano, corresponde a la del octaedro (normal o distorsionado), además del prisma trigonal. Algunos de tantos ejemplos de compuestos con este número de coordinación son:
-[AlF6]3-
-[Co(NH3)6]3+
-[Zr(CH3)6]2-
-NaCl (sí, la sal de mesa)
-MoS2, nótese que C.N. para este compuesto no es 2
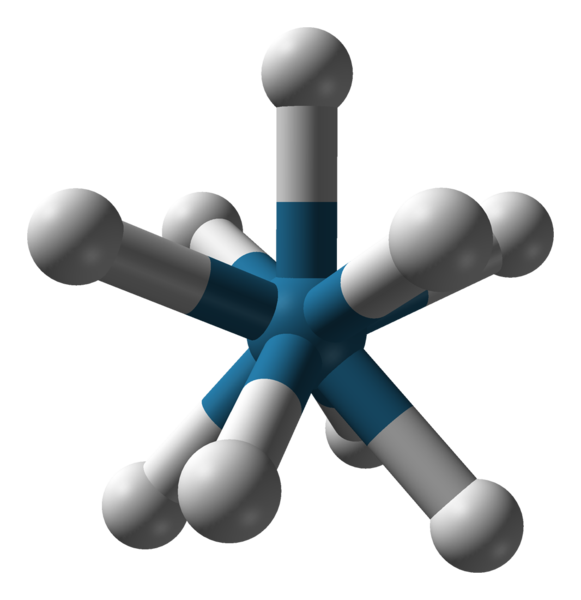
Existen otros números de coordinación, desde el 7 hasta el 15. Para que C.N. sea alto, el ion o átomo central debe ser muy grande, tener poca carga, y al mismo tiempo los ligandos deben ser muy pequeños. Algunos ejemplos de compuestos con tales C.N. son a continuación y para finalizar:
-K3[NbOF6], C.N. 7 y geometría octaedro apicado
-[Mo(CN)8]3-
-[Zr(ox)4]2-, siendo ox el ligando oxalato
-[ReH9]2-
-[Ce(NO3)6]2-, C.N. igual a 12
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
- Shiver & Atkins. (2008). Química Inorgánica. (Cuarta edición). Mc Graw Hill.
- Wikipedia. (2020). Coordination number. Recuperado de: en.wikipedia.org
- The Editors of Encyclopaedia Britannica. (s.f.). Coordination number. Recuperado de: britannica.com
- Prof. Robert J. Lancashire. (15 de agosto de 2020). Coordination Numbers and Geometry. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
- Helmenstine, Anne Marie, Ph.D. (28 de agosto de 2020). Coordination Number Definition in Chemistry. Recuperado de: thoughtco.com
