Axiomas de probabilidad: tipos, explicación, ejemplos, ejercicios
Los axiomas deprobabilidad son proposiciones matemáticas referentes a la teoría de la probabilidad, que no ameritan demostración. Los axiomas fueron establecidos en 1933 por el matemático ruso Andrei Kolmogorov (1903-1987) en su obra Fundamentos de la Teoría de la Probabilidad y sentaron las bases del estudio matemático de la probabilidad.
Al llevar a cabo un cierto experimento aleatorio ξ, el espacio muestral E es el con junto de todos los resultados posibles del experimento, llamados también eventos. Un evento cualquiera se denota como A y P(A) es la probabilidad de que ocurra. Entonces Kolmogorov estableció que:

–Axioma 1 (no negatividad): la probabilidad de que ocurra cualquier suceso A siempre es positiva o cero, P(A) ≥0. Cuando la probabilidad de un suceso es 0, se le llama suceso imposible.
–Axioma 2 (certidumbre): siempre que algún evento que pertenece a E, su probabilidad de ocurrencia es 1, lo cual podemos expresar como P(E) = 1. Es lo que se conoce como un suceso seguro, ya que al realizar un experimento, con toda certeza hay un resultado.
–Axioma 3 (adición): en el caso de dos o más eventos incompatibles dos a dos, llamados A1, A2, A3…, la probabilidad de que ocurra el suceso A1 más el A2 más el A3 y así sucesivamente, es la suma de las probabilidades de que suceda cada uno separadamente.
Esto se expresa como: P(A1 U A2 U A3 U…) = P(A1) + P(A2) + P(A3) +…

Índice del artículo
Los axiomas de probabilidad se utilizan ampliamente en multitud de aplicaciones. Por ejemplo:
Se lanza una chincheta o tachuela al aire, y al caer al piso está la opción de caer con la punta hacia arriba (U) o con la punta hacia abajo (D) (no consideraremos otras posibilidades). El espacio muestral de este experimento consta de estos eventos, luego E = {U,D}.

Al aplicar los axiomas tenemos:
P(E) = 1 (Axioma 2)
Pero P(E) = P(U) + P(D) (Axioma 3), porque estos eventos son mutuamente incompatibles, o disjuntos. La chincheta no cae con la punta hacia arriba o hacia abajo al mismo tiempo, es uno o lo otro, pero no ambos, ya que no se están considerando otras posibilidades. Entonces:
P(U) + P(D) = 1
P(U) = 1 – P(D)
Si es igualmente probable que caiga con la punta hacia arriba o hacia abajo, P(U) = P(D) = ½ (Axioma 1). Sin embargo, puede ser que por la construcción y el diseño de la chincheta sea más probable que caiga de una manera o de otra. Por ejemplo, puede ser que P(U) = ¾ mientras que P(D) = ¼ (Axioma 1).
Nótese que en ambos casos, la suma de las probabilidades da 1. Sin embargo, los axiomas no indican la manera de asignar las probabilidades, al menos no completamente. Pero sí afirman que son números comprendidos entre 0 y 1 y que, tal como ocurre en este caso, la suma de todas es 1.
Los axiomas de probabilidad no constituyen un método de asignar el valor de la probabilidad. Para esto hay tres opciones que son compatibles con los axiomas:
A cada evento se le asigna la misma probabilidad de suceder, entonces se define la probabilidad de ocurrencia como:
P(A) = número de casos favorables al evento A/ número de casos posibles
Por ejemplo, ¿cuál es la probabilidad de extraer un as de un mazo de cartas francesas? El mazo tiene 52 cartas, 13 de cada palo y son 4 palos. Cada palo tiene 1 as, por lo que en total son 4 ases:
P(as) = 4/52 = 1/13
La regla de Laplace está limitada a espacios muestrales finitos, donde cada evento es igualmente probable.
Aquí el experimento tiene que ser repetible, ya que el método se fundamenta en realizar un gran número de repeticiones.
Hagamos i repeticiones del experimento ξ, del cual encontramos que n es el número de veces que ocurre determinado evento A, entonces la probabilidad de que este evento ocurra es:
P(A) = limi→∞ (n/i)
Donde n/i es la frecuencia relativa de un suceso.
Definir P(A) de esta manera satisface los axiomas de Kolmogorov, pero tiene el inconveniente de que hay que realizar muchas pruebas para que la probabilidad sea apropiada.
Método subjetivo
Una persona o un grupo de personas pueden acordar en asignar la probabilidad a un suceso, mediante sus propios juicios. Este método tiene la desventaja de que distintas personas pueden asignar probabilidades distintas a un mismo evento.
En el experimento de lanzar simultáneamente 3 monedas honradas, obtener las probabilidades de los eventos descritos:
a) 2 caras y una cruz.
b) 1 cara y dos cruces
c) 3 cruces.
d) Al menos 1 cara.
Las caras se denotan con C y las cruces con X. Pero hay varias maneras de obtener dos caras y una cruz. Por ejemplo, las dos primeras monedas pueden caer con cara y la tercera con cruz. O la primera puede caer cara, la segunda cruz y la tercera cara. Y finalmente la primera puede ser cruz y las restantes caras.
Para responder a las preguntas es necesario conocer todas las posibilidades, las cuales se describen en una herramienta llamada diagrama de árbol o árbol de probabilidades:
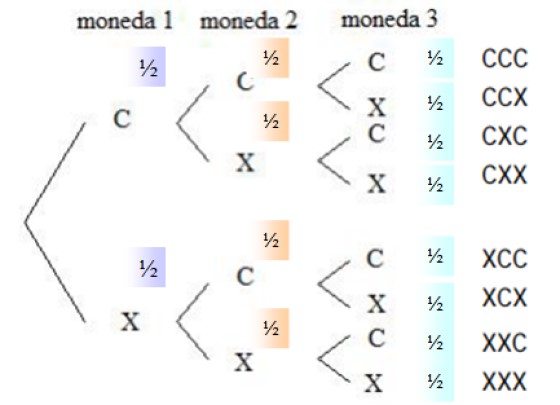
La probabilidad de que en una moneda cualquiera salga cara es ½, lo mismo sucede para las cruces, ya que la moneda es honesta. En la columna de la derecha están listadas todas las posibilidades que tiene el lanzamiento, esto es, el espacio muestral.
Del espacio muestral se escogen las combinaciones que respondan al suceso pedido, ya que el orden en que aparecen las caras no es importante. Hay tres eventos favorables: CCX, CXC y XCC. La probabilidad de que suceda cada evento es:
P (CCX) = ½. ½ . ½ = 1/8
Igual sucede para los eventos CXC y XCC, cada uno tiene 1/8 de probabilidad de suceder. Por lo tanto la probabilidad de obtener exactamente 2 caras es la suma de las probabilidades de todos los sucesos favorables:
P (2 caras) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375
Solución b
Hallar la probabilidad de que se den exactamente dos cruces es un problema análogo al anterior, también hay tres eventos favorables tomados del espacio muestral: CXX, XCX y XXC. Por lo tanto:
P (2 cruces) = 3/8 = 0.375
Solución c
Intuitivamente sabemos que la probabilidad de obtener 3 cruces (o 3 caras) es menor. En este caso el evento buscado es XXX, al final de la columna derecha, cuya probabilidad es:
P (XXX) = ½. ½. ½ = 1/8 = 0.125.
Solución d
Se pide obtener al menos 1 cara, esto significa que pueden salir 3 caras, 2 caras o 1 cara. El único evento incompatible con esto es aquel en que salen 3 cruces, cuya probabilidad es 0.125. Por lo tanto la probabilidad buscada es:
P (al menos 1 cara) = 1 – 0.125 = 0.875.
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Lipschutz, S. 1991. Serie Schaum: Probabilidad. McGraw Hill.
- Obregón, I. 1989.Teoría de la probabilidad. Editorial Limusa.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
