Vectores concurrentes: características, ejemplos y ejercicios
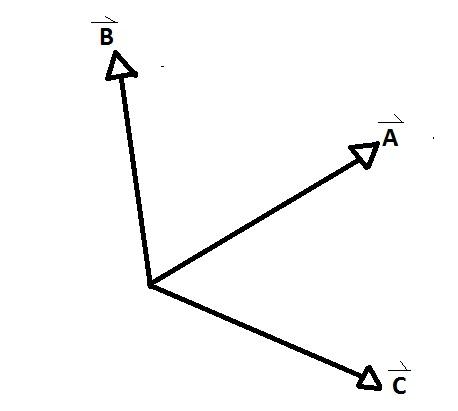
Los vectores concurrentes son los grupos de vectores cuyos ejes coinciden en un punto, formándose entre cada par de ellos un ángulo interno y otro externo. Un ejemplo claro se observa en la figura inferior, donde A, B y C son vectores concurrentes entre sí.
D y E a diferencia del resto no lo son. Existen ángulos formados entre los vectores concurrentes AB, AC y CB. Se denominan ángulos de relación entre los vectores.
Índice del artículo
- 1 Características
- 2 Tipos de vectores
- 3 Notación de vectores
- 4 Operaciones con vectores concurrentes
- 5 Ejemplos: ejercicios resueltos
- 6 Ejercicios propuestos
- 7 Referencias
-Tienen un punto en común, el cual coincide con su origen: todas las magnitudes de los vectores concurrentes parten de un punto en común hasta sus respectivos extremos.
-El origen es considerado como el punto de acción del vector: se debe establecer un punto de acción el cual será directamente afectado por cada uno de los vectores concurrentes.
-Su dominio en el plano y espacio es R2 y R3 respectivamente: los vectores concurrentes son libres de cubrir todo el espacio geométrico.
-Permite diferentes notaciones en un mismo grupo de vectores. Según las ramas de estudio, diferentes notaciones se hacen presentes en las operaciones con vectores.
La rama de los vectores posee múltiples subdivisiones, entre algunos se pueden nombrar: los paralelos, perpendiculares, coplanarios, correspondientes, opuestos y unitarios. Los vectores concurrentes figuran en esta lista y al igual que todos los nombrados anteriormente, tienen muchas aplicaciones en distintas ciencias.
Son muy comunes en el estudio de vectores, debido a que representan una generalización provechosa en las operaciones con los mismos. Tanto en el plano como en el espacio, los vectores concurrentes son de uso corriente para la representación de diferentes elementos y estudiar su influencia en un sistema particular.
Existen diversas formas de representar un elemento vectorial. Las principales y más conocidas son:
Propuesta por este mismo enfoque matemático, denota a los vectores con una terna correspondiente a las magnitudes de cada eje ( x , y , z )
A : ( 1 , 1 , -1 ) Espacio A : ( 1 , 1 ) Plano
Sirven únicamente para denotar vectores en el plano, aunque en el cálculo integral se le asigna la componente de profundidad. Se compone con una magnitud lineal r y un ángulo con respecto al eje polar Ɵ.
A : ( 3 , 450 ) Plano A : ( 2 , 450 , 3 ) Espacio
Definen las magnitudes del vector mediante los versores. Los versores ( i + j + k ) representan a los vectores unitarios correspondientes a los ejes X, Y y
A : 3i + 2j – 3k
Son similares a la notación polar, pero con la adición de un segundo ángulo que barre sobre el plano xy simbolizado por δ.
A : ( 4 , 60o , π/4 )
Los vectores concurrentes son mayormente usados para definir operaciones entre vectores, debido a que resulta más sencillo comparar los elementos de los vectores cuando estos se presentan de manera concurrente.
La suma de vectores concurrentes tiene como fin encontrar el vector resultante Vr. El cual, según la rama de estudio, corresponde a una acción final
Por ejemplo: Se atan 3 cuerdas { A , B , C } a una caja, cada extremo de la cuerda está en manos de un sujeto. Cada uno de los 3 sujetos debe jalar la cuerda en una dirección distinta a los otros 2.
A : ( ax , ay , az ) B : ( bx , by , bz ) C : ( cx , cy , cz )
A + B + C = ( ax+bx+cx ; ay+by+cy ; az+bz+cz ) = Vr
La caja solo podrá moverse en una sola dirección, por lo tanto Vr indicará la dirección y sentido del desplazamiento de la caja.
Existen muchos criterios con respecto a la diferencia entre vectores, muchos autores optan por excluirla y afirman que solo se estipula la suma entre vectores, donde la diferencia se trata de la suma del vector opuesto. Lo cierto es que algebraicamente los vectores pueden restarse.
A : ( ax , ay , az ) B : ( bx , by , bz )
A – B = A + (-B) = ( ax-bx ; ay-by ; az-bz ) = [ ax + (-bx) ; ay + (-by) ; az + (-bz) ]
También conocido como producto punto, genera un valor escalar que puede ser relacionado con varias magnitudes según la rama de estudio.
Para la geometría indica el área del paralelogramo formado por el par de vectores concurrentes a través del método del paralelogramo. Para la física mecánica define el trabajo realizado por una fuerza F al desplazar un cuerpo una distancia Δr.
ѡ = F . Δr
Tal cual su nombre lo indica genera un valor escalar y se define de la siguiente manera:
Sean los vectores A y B
A : ( ax , ay , az ) B : ( bx , by , bz )
-Forma analítica:
( A . B ) = |A|.|B|.Cos θ
Donde θ es el ángulo interno entre ambos vectores
-Forma algebraica:
( A . B ) = ( ax.bx + ay.by + az.bz )
El producto vectorial o producto punto entre dos vectores, define un tercer vector C que tiene la cualidad de ser perpendicular a B y C. En la física define el vector torque τ elemento base de la dinámica rotacional.
-Forma analítica:
| A x B | = |A|.|B|.Sen θ
-Forma algebraica:
( A x B ) = = (ax . by – ay . bx) – (ax . bz – az . bx) j + ( ax . by – ay . bx ) k
-Movimiento relativo: rA/B
La base de la relatividad es el movimiento relativo y los vectores concurrentes son la base del movimiento relativo. Se pueden deducir posiciones, velocidades y aceleraciones relativas aplicando el siguiente orden de ideas.
r A/B = rA – rB ; Posición relativa de A respecto a B
v A/B = vA – vB ; Velocidad relativa de A respecto a B
a A/B = aA – aB ; Aceleración relativa de A respecto a B
Sean A, B y C vectores concurrentes.
A = ( -1 , 3 , 5 ) B = ( 3 , 5 , -2 ) C = ( -4 , -2 , 1)
-Definir el vector resultante Vr = 2A – 3B + C
2A = ( 2(-1) , 2(3) , 2(5) ) = ( -2 , 6 , 10 )
-3B = ( -3(3) , -3(5) , -3(-2) ) = ( -9 , -15 , 6 )
Vr = 2A + (-3B) + C = ( -2 , 6 , 10 ) + ( -9 , -15 , 6 ) + ( -4 , -2 , 1)
Vr = ( [-2+(-9)+(-4)] ; [6+(-15)+(-2)] ; (10+6+1) )
Vr = ( -15 , -11 , 17 )
-Definir el producto escalar ( A . C )
( A . C ) = ( -1 , 3 , 5 ) . ( -4 , -2 , 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 – 6 + 5
( A . C ) = 3
-Calcular el ángulo entre A y C
( A . C ) = |A|.|C|.Cos θ Donde θ es el ángulo más corto entre los vectores
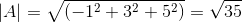
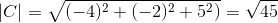
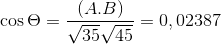
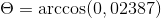
θ = 88,630
-Encontrar un vector perpendicular a A y B
Para esto es necesario definir el producto vectorial entre ( -1 , 3 , 5 ) y ( 3 , 5 , -2 ). Tal como se explicó antes, se construye una matriz de 3 x 3 donde las primera fila está compuesta por la terna de vectores unitarios ( i , j , k ). Luego la 2da y 3era fila la componen los vectores a operar, respetando el orden operacional.
( A x B ) = = [ (-1) . 5 – (3 . 3) ] i – [ (-1) . (-2) – (5 . 3) ] j + [ (-1) . 5 – (3 . 3) ] k
( A x B ) = ( -5 – 9) I – ( 2 – 15 ) j + ( -5 – 9 ) k
( A x B ) = –14 I + 13 j – 14 k
Sean Va y Vb los vectores velocidad de A y B respectivamente. Calcular la velocidad de B visto desde A.
Va = ( 3 , -1 , 5 ) Vb = ( 2 , 5 , -3 )
En este caso se pide la velocidad relativa de B respecto de A VB/A
VB/A = VB – VA
VB/A = ( 2 , 5 , -3 ) – ( 3 , -1 , 5 ) = ( -1 , 6 , -8 )
Este es el vector velocidad de B visto desde A. Donde se describe un nuevo vector de la velocidad de B tomando referencia de un observador posicionado en A y desplazándose con la velocidad de A.
1-Construya 3 vectores A, B y C que sean concurrentes y relacione 3 operaciones entre ellos mediante un ejercicio práctico.
2-Sean los vectores A : ( -2 , 4 , -11 ), B : ( 1 , -6 , 9 ) y C : ( -2 , -1 , 10 ). Encuentre vectores perpendiculares a: A y B, C y B, La suma A + B + C.
4-Determine 3 vectores que sean perpendiculares entre sí, sin tomar en cuenta los ejes coordenados.
5-Defina el trabajo realizado por una fuerza que levanta un bloque de 5 kg de masa, desde el fondo de un pozo de 20m de profundidad.
6-Demuestre de manera algebraica que la resta de vectores es igual a la suma del vector opuesto. Justifique sus postulados.
7-Denote un vector en todas las notaciones desarrolladas en este artículo. ( Cartesiana, polar, analítica y esférica).
8-Las fuerzas magnéticas ejercidas sobre un imán que reposa en una mesa, está dada por los vectores siguientes; V : ( 5 , 3 ,-2 ), T : ( 4 , 7 ,9 ), H : ( -3 , 5 , -4 ). Determine en qué dirección se moverá el imán si todas las fuerzas magnéticas actúan al mismo tiempo.
- Euclidean Geometry and Transformations. Clayton W. Dodge. Courier Corporation, 1 ene. 2004
- How to Solve Applied Mathematics Problems L. Moiseiwitsch. Courier Corporation, 10 abr. 2013
- Basic Concepts of Geometry. Walter Prenowitz, Meyer Jordan. Rowman & Littlefield, 4 oct. 2012
- Los vectores. Rocío Navarro Lacoba, 7 jun. 2014
- Álgebra lineal. Bernard Kolman, David R. Hill. Pearson Educación, 2006
