Ondas unidimensionales: expresión matemática y ejemplos
Las ondas unidimensionales son las que se propagan en una sola dirección sin importar que la vibración ocurra o no en la misma dirección de propagación. Un buen ejemplo de ellas es la onda que se desplaza por una cuerda tensa como la de una guitarra.
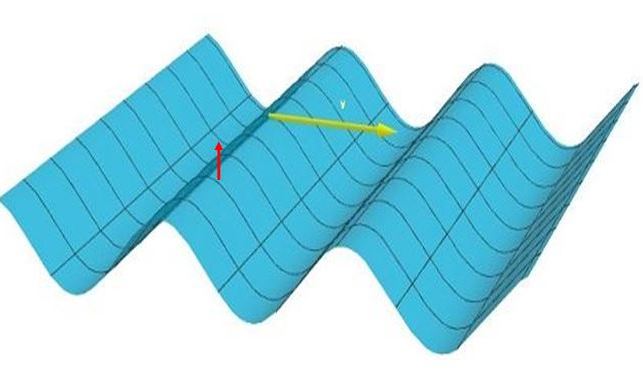
En una onda plana transversal, las partículas vibran en dirección vertical (suben y bajan, ver la flecha roja en la figura 1), pero es unidimensional porque la perturbación viaja en una sola dirección, siguiendo la flecha amarilla.
Las ondas unidimensionales aparecen con bastante frecuencia en la cotidianidad. En el apartado siguiente se describen algunos ejemplos de ellas y también de ondas que no son unidimensionales, para establecer con claridad las diferencias.
Índice del artículo
- 1 Ejemplos de ondas unidimensionales y ondas no unidimensionales
- 2 Expresión matemática de una onda unidimensional
- 3 Referencias
Estos son algunos ejemplos de ondas unidimensionales que pueden observarse fácilmente:
– Un pulso de sonido que viaja por una barra recta, ya que se trata de una perturbación que se propaga a todo lo largo de la barra.
– Una onda que viaja por un canal de agua, aun cuando el desplazamiento de la superficie del agua no sea paralelo al canal.
– Ondas que se propagan sobre una superficie o por el espacio tridimensional también pueden ser unidimensionales, siempre que sus frentes de ondas sea planos paralelos entre sí y viajen en una sola dirección.
Un ejemplo de onda no unidimensional se encuentra en las olas que se forman en una superficie de agua quieta cuando se deja caer una piedra. Se trata de una onda en dos dimensiones con frente de onda cilíndrico.

Otro ejemplo de onda no-unidimensional es la onda de sonido que genera un petardo haciendo explosión a cierta altura. Esta se trata de una onda tridimensional con frentes de onda esféricos.
La forma más general de expresar una onda unidimensional que se propaga sin atenuación en la dirección positiva del eje x y con velocidad v es, matemáticamente:
y(x,t) = f(x – v.t)
En esta expresión y representa la perturbación en la posición x al instante t. La forma de la onda está dada por la función f. Por ejemplo la función de la onda mostrada en la figura 1 es: y(x,t) = cos( x – v t) y la imagen de la onda corresponde al instante t=0.
Una onda como esta, descrita por una función coseno o seno, se denomina onda armónica. Aunque no es la única forma de onda que existe, es de suma importancia, porque cualquier otra onda puede representarse como una superposición o suma de ondas armónicas. Se trata del conocido teorema de Fourier, tan utilizado para describir señales de todo tipo.
Cuando la onda viaja en la dirección negativa del eje x, simplemente se cambia v por -v en argumento, quedando:
y(x,t) = g(x + v t)
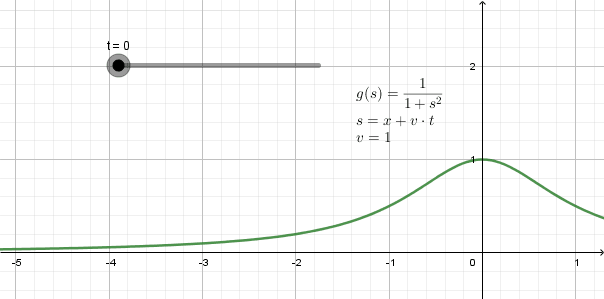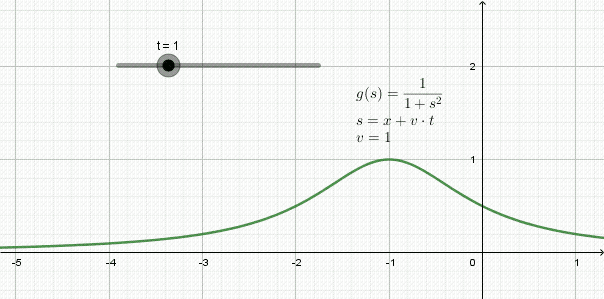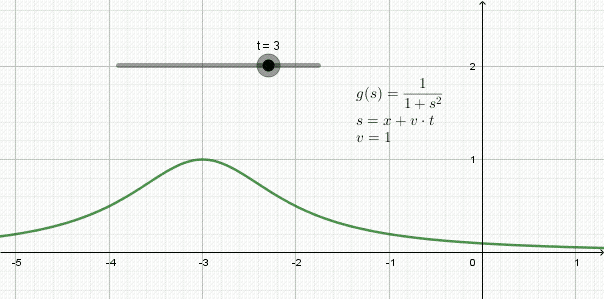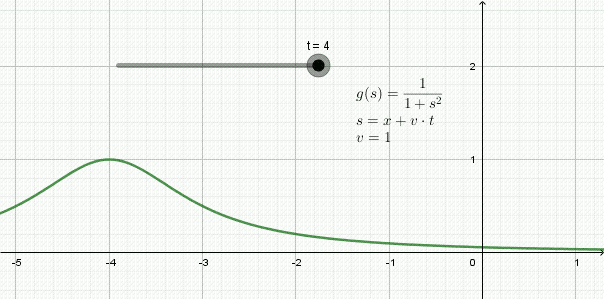
En la figura 3 se aprecia la animación de una onda que viaja hacia la izquierda: se trata de una forma llamada función lorentziana y su expresión matemática es:
y(x,t) = 1 / (1 + (x + 1⋅t)2
En este ejemplo la rapidez de propagación es v=1, -una unidad de espacio por cada unidad de tiempo-.
La ecuación de onda es una ecuación en derivadas parciales, cuya solución es desde luego una onda. Establece la relación matemática entre la parte espacial y la parte temporal de la misma, y tiene la forma:
A continuación se tiene la expresión general y (x,t) para una onda armónica:
y(x,t) = A⋅cos(k⋅x ± ω⋅t + θo)
a) Describa el significado físico de los parámetros A, k, ω y θo.
b) ¿Qué significado tienen los signos ± en el argumento del coseno?
c) Verifique que la expresión dada es en efecto la solución de la ecuación de onda del apartado anterior y encuentre la velocidad v de propagación.
Solución a)
Las características de la onda se encuentran en los siguientes parámetros:
-A representa la amplitud o “altura de la onda”.
-k es en número de onda y se relaciona con la longitud de onda λ mediante k=2π/ λ.
-ω es la frecuencia angular y se relaciona con el periodoT de oscilación de la onda mediante
ω = 2π/ T.
-θo es la fase inicial, la cual tiene relación con el punto de partida de la onda.
Solución b)
Se toma signo negativo si la onda viaja en la dirección positiva del eje X y signo positivo en caso contrario.
Solución c)
Verificar que la expresión dada es solución de la ecuación de onda es simple: se toma la derivada parcial de la función y(x,t) respecto a x dos veces, se vuelve a derivar parcialmente respecto a t dos veces y luego se reúnen ambos resultados para obtener una igualdad:
Derivada segunda respecto a x: ∂2y/ ∂x2= -k2. A⋅cos (k⋅x ± ω⋅t + θo)
Derivada segunda respecto a t: ∂2y/ ∂t2= -ω2. A⋅cos (k⋅x ± ω⋅t + θo)
Se sustituyen estos resultados en la ecuación de onda:
-k2. A⋅cos (k⋅x ± ω⋅t + θo) = (1/v2) (-ω2. A⋅cos (k⋅x ± ω⋅t + θo))
Tanto A como el coseno se simplifican, ya que aparecen a ambos lados de la igualdad y el argumento del coseno es el mismo, por lo tanto la expresión se reduce a:
-k2 = (1/v2) (-ω2)
Que permite obtener una ecuación para v en términos de ω y k:
v2 = ω2 / k2
v = ± ω / k
- E-educativa. Ecuación de las ondas armónicas unidimensionales. Recuperado de: e-ducativa.catedu.es
- El rincón de la Física. Clases de Ondas. Recuperado de: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Ondas y Física Cuántica. Serie: Física para Ciencias e Ingeniería. Editado por Douglas Figueroa. Universidad Simón Bolívar. Caracas, Venezuela.
- Fisica Lab. Movimiento ondulatorio. Recuperado de: fisicalab.com.
- Peirce, A. Lecture 21: The one dimensional Wave Equation: D’Alembert’s Solution. Recuperado de: ubc.ca.
- Wave equation. Recuperado de: en.wikipedia.com
