Principio multiplicativo: técnicas de conteo y ejemplos
¿Qué es el principio multiplicativo?
El principio multiplicativo es una técnica que se utiliza para resolver problemas de conteo para hallar la solución sin que sea necesario enumerar sus elementos. Es conocido también como el principio fundamental del análisis combinatorio; se basa en la multiplicación sucesiva para determinar la forma en la que puede ocurrir un evento.
Este principio establece que, si una decisión (d1) puede ser tomada de n maneras y otra decisión (d2) puede tomarse de m maneras, el número total de maneras en las que pueden ser tomadas las decisiones d1 y d2 será igual a multiplicar de n * m. Según el principio, cada decisión se realiza una tras otra: número de maneras = N1 * N2… * Nx maneras.
Ejemplos
Ejemplo 1
Paula planea ir al cine con sus amigas, y para escoger la ropa que usará, separo 3 blusas y 2 faldas. ¿De cuántas maneras se puede vestir Paula?

Solución
En este caso, Paula debe tomar dos decisiones:
d1 = Escoger entre 3 blusas = n
d2 = Escoger entre 2 faldas = m
De esa forma Paula tiene n * m decisiones a tomar o maneras diferentes de vestirse.
n * m = 3* 2 = 6 decisiones.
El principio multiplicativo nace de la técnica del diagrama del árbol, que se trata de un diagrama que relaciona todos los posibles resultados, de manera que cada uno pueda ocurrir un número finito de veces.
Ejemplo 2
Mario tenía mucha sed, así que fue a la panadería a comprar un jugo. Luis lo atiende y le dice que tiene en dos tamaños: grande y pequeño; y cuatro sabores: manzana, naranja, limón y uva. ¿De cuántas maneras puede Mario escoger el jugo?
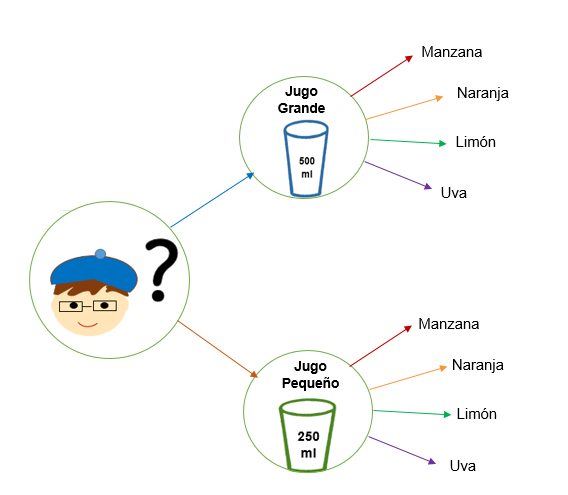
Solución
En el diagrama puede observarse que Mario tiene 8 maneras distintas para escoger el jugo y que, al igual que en el principio multiplicativo, este resultado se obtiene por la multiplicación de n*m. La única diferencia es que a través de este diagrama puede saberse cómo son las maneras en que Mario escoge el jugo.
Por otra parte, cuando el número de resultados posibles es muy grande, resulta más práctico utilizar el principio multiplicativo.
Técnicas de conteo
Las técnicas de conteo son métodos usados para hacer un conteo directo, y así saber el número de posibles arreglos que pueden tener los elementos de un conjunto determinado. Estas técnicas están basadas en varios principios:
Principio de adición
Este principio establece que, si dos eventos m y n no pueden ocurrir al mismo tiempo, el número de formas como puede ocurrir el primer o segundo evento será la suma de m + n:
Número de formas = m + n… + x formas diferentes.
Ejemplo
Antonio quiere hacer un viaje pero no decide a cuál destino; en la Agencia de Turismo del Sur le ofrecen una promoción para viajar a New York o Las Vegas, mientras que la Agencia de Turismo del Este le recomienda viajar a Francia, Italia o España. ¿Cuántas alternativas de viajes diferentes le ofrecen Antonio?
Solución
Con la Agencia de Turismo del Sur Antonio tiene 2 alternativas (New York o Las Vegas), mientras que con la Agencia de Turismo del Este tiene 3 opciones (Francia, Italia o España). El número de alternativas diferentes es:
Número de alternativas= m + n = 2 + 3 = 5 alternativas.
Principio de permutación
Se trata de ordenar específicamente todos o algunos de los elementos que forman un conjunto, para facilitar el conteo de todos los posibles arreglos que pueden hacerse con los elementos.
El número de permutaciones de n elementos diferentes, tomados todos a la vez, se representa como:
nPn = n!
Ejemplo
Cuatro amigos quieren tomarse una fotografía y desean saber de cuántas formas diferentes pueden ordenarse.
Solución
Se quiere conocer el conjunto de todas las formas posibles en que las 4 personas se pueden colocar para tomarse la fotografía. Así, se tiene que:
4P4 = 4! = 4*3*2*1 = 24 formas diferentes.
Si el número de permutaciones de n elementos disponibles es tomado por partes de un conjunto que está formado por r elementos, se representa como:
nPr = n! ÷ (n – r)!
Ejemplo
En una sala de aula se tienen 10 puestos. Si para la clase asisten 4 estudiantes, ¿de cuántas maneras distintas los estudiantes pueden ocupar los puestos?
Solución
Se tiene que el número total del conjunto de sillas es 10, y de estas solo serán usadas 4. Se aplica la fórmula dada para determinar el número de permutaciones:
nPr = n! ÷ (n – r)!
10P4 = 10! ÷ (10 – 4)!
10P4 = 10! ÷ 6!
10P4= 10* 9*8*7*6*5*4*3*2*1 ÷ 6*5*4*3*2*1 = 5040 maneras de ocupar los puestos.
Existen casos en los que algunos de los elementos disponibles de un conjunto se repiten (son iguales). Para calcular el número de arreglos tomando todos los elementos a la vez se utiliza la siguiente fórmula:
nPr = n! ÷ n1!* n2!… nr!
Ejemplo
¿Cuántas palabras diferentes de cuatro letras pueden ser formadas a partir de la palabra “lobo”?
Solución
En este caso se tienen 4 elementos (letras) de los cuales dos de ellos son exactamente iguales. Aplicando la fórmula dada, se sabe cuántas palabras diferentes resultan:
nPr = n! ÷ n1!* n2!… nr!
4P2, 1,1 = 4! ÷ 2!*1!*1!
4P2, 1, 1 = (4*3*2*1) ÷ (2*1)*1*1
4P2, 1, 1 = 24 ÷ 2 = 12 palabras diferentes.
Principio de combinación
Se trata de arreglar todos o algunos de los elementos que forman un conjunto sin un orden específico. Por ejemplo, si se tiene un arreglo XYZ, este será idéntico a los arreglos ZXY, YZX, ZYX, entre otros; esto es porque, a pesar de no estar en el mismo orden, los elementos de cada arreglo son los mismos.
Cuando se toman algunos elementos (r) del conjunto (n), el principio de combinación es dado por la siguiente fórmula:
nCr = n! ÷ (n – r)!r!
Ejemplo
En una tienda venden 5 tipos diferentes de chocolate. ¿De cuántas formas diferentes se pueden escoger 4 chocolates?
Solución
En este caso se tienen que escoger 4 chocolates de los 5 tipos que venden en la tienda. El orden en que son elegidos no importa y, además, puede escogerse más de dos veces un tipo de chocolate. Aplicando la formula, se tiene que:
nCr = n! ÷ (n – r)!r!
5C4 = 5! ÷ (5 – 4)! 4!
5C4 = 5! ÷ (1)!4!
5C4 = 5*4*3*2*1 ÷ 4*3*2*1
5C4 = 120 ÷ 24 = 5 maneras diferentes de escoger 4 chocolates.
Cuando se toman todos los elementos (r) del conjunto (n), el principio de combinación es dado por la siguiente fórmula:
nCn = n!
Ejercicios resueltos
Ejercicio 1
Se tiene un equipo de béisbol con 14 integrantes. ¿De cuántas maneras se pueden asignar 5 posiciones para un juego?
Solución
El conjunto está integrado por 14 elementos y se quiere asignar 5 posiciones específicas; es decir, que el orden importa. Se aplica la fórmula de permutación donde n elementos disponibles son tomados por partes de un conjunto que está formado por r.
nPr = n! ÷ (n – r)!
Donde n = 14 y r = 5. Se sustituye en la fórmula:
14P5 = 14! ÷ (14 – 5)!
14P5 = 14! ÷ (9)!
14P5 = 240 240 maneras de asignar las 9 posiciones del juego.
Ejercicio 2
Si una familia de 9 integrantes va de viaje y compra sus boletos con los puestos consecutivos, ¿de cuántas formas diferentes pueden sentarse?
Solución
Se trata de 9 elementos que van a ocupar 9 asientos de forma consecutiva.
P9 = 9!
P9 = 9*8*7*6*5*4*3*2*1 = 362 880 maneras diferentes de sentarse.
Referencias
- Hopkins, B. (2009). Resources for Teaching Discrete Mathematics: Classroom Projects, History Modules, and Articles.
- Johnsonbaugh, R. (2005). Matemáticas discretas. Pearson Educación,.
- Lutfiyya, L. A. (2012). Finite and Discrete Math Problem Solver. Research & Education Association Editors.
- Padró, F. C. (2001). Matemática discreta. Politèc. de Catalunya.
- Steiner, E. (2005). Matemáticas para las ciencias aplicadas. Reverte.
