Primos relativos: qué son, explicación, ejemplos
Se llama primos relativos (coprimos o primos relativos entre sí) a cualquier par de números enteros que no tienen ningún divisor en común, excepto el 1. Dicho en otras palabras, dos números enteros son primos relativos si en sus descomposiciones en números primos, no tienen ningún factor en común.
Por ejemplo, si se escogen el 4 y el 25, las descomposiciones en factores primos de cada uno son 2² y 5² respectivamente. Como se aprecia, estos no poseen ningún factor común, por lo tanto, 4 y 25 son primos relativos.
Por otro lado, si se escogen el 6 y el 24, al realizar sus descomposiciones en factores primos se obtiene que 6=2*3 y 24=2³*3.
Como se puede ver, estas últimas dos expresiones poseen al menos un factor en común, por lo tanto, no son primos relativos.
Características de los primos relativos
Un detalle con el que hay que tener cuidado, es que al decir que un par de números enteros son primos relativos es que eso no implica que ninguno de ellos sea un número primo.
Por otro lado, la definición de arriba se puede resumir de la siguiente forma: dos números enteros “a” y “b” son primos relativos si, y solo si, el máximo común divisor de estos es el 1, es decir, mcd(a, b)=1.
Dos conclusiones inmediatas de esta definición son que:
-Si “a” (o “b”) es un número primo, entonces mcd(a,b)=1.
-Si “a” y “b” son números primos, entonces mcd(a,b)=1.
Es decir, que si al menos uno de los números escogidos es un número primo, entonces directamente el par de números son primos relativos.
Otras características
Otros resultados que se utilizan para determinar si dos números son primos relativos son:
-Si dos números enteros son consecutivos, entonces estos son primos relativos.
-Dos números naturales “a” y “b” son primos relativos si, y solo si, los números “(2^a)-1” y “(2^b)-1” son primos relativos.
-Dos números enteros “a” y “b” son primos relativos si, y solo si, al graficar el punto (a, b) en el plano cartesiano, y construir la recta que pasa por el origen (0,0) y (a, b), esta no contiene ningún punto con coordenadas enteras.
Ejemplos
1.- Considere los números enteros 5 y 12. Las descomposiciones en factores primos de ambos números son: 5 y 2²*3 respectivamente. En conclusión, mcd(5,12)=1, por lo tanto, 5 y 12 son primos relativos.
2.- Sean los números -4 y 6. Entonces -4=-2² y 6=2*3, de modo que el mcd(-4,6)=2≠1. En conclusión -4 y 6 no son primos relativos.
Si se procede a graficar la recta que pasa por los pares ordenados (-4,6) y (0,0), y a determinar la ecuación de dicha recta, se puede verificar que esta pasa por el punto (-2,3).
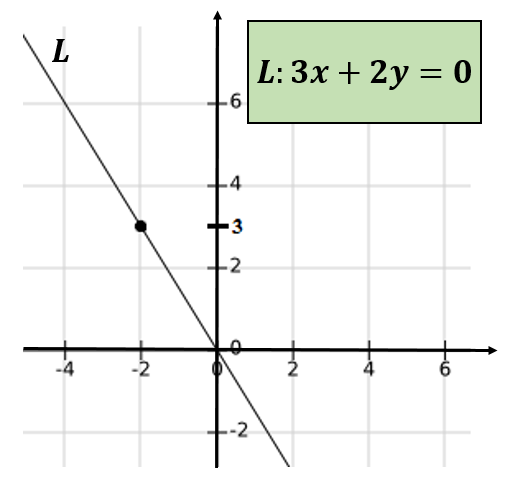
Nuevamente, se concluye que -4 y 6 no son primos relativos.
3.- Los números 7 y 44 son primos relativos y se puede concluir rápidamente gracias a lo dicho arriba, pues 7 es un número primo.
4.- Considere los números 345 y 346. Al ser dos números consecutivos se verifica que mcd(345,346)=1, por lo tanto, 345 y 346 son primos relativos.
5.- Si se consideran los números 147 y 74, entonces estos son primos relativos, ya que 147=3*7² y 74=2*37, por lo tanto, el mcd(147,74)=1.
6.- Los números 4 y 9 son primos relativos. Para demostrarlo se puede utilizar la segunda caracterización mencionada arriba. En efecto, 2^4 -1= 16-1=15 y 2^9-1=512-1=511.
Los números obtenidos son 15 y 511. Las descomposiciones en factores primos de estos números son 3*5 y 7*73 respectivamente, de modo que mcd(15,511)=1.
Como se puede notar, utilizar la segunda caracterización es un trabajo más largo y trabajoso que verificarlo directamente.
7.- Considere los números -22 y -27. Entonces estos números se pueden reescribir como sigue: -22=-2*11 y -27=-3³. Por tanto, el mcd(-22,-27)=1, así que -22 y -27 son primos relativos.
