Sumatoria telescópica: cómo se resuelve y ejercicios resueltos
La sumatoria telescópica es una rama de las operaciones con series numéricas. Aborda las sumatorias de elementos desde un valor inicial hasta “n” de expresiones cuya argumento obedece a cualquiera de los siguientes patrones:
(Fx – Fx+1);( Fx+1 – Fx)

Como también:
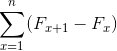

Representan una sumatoria de elementos que al desarrollarse, es sometida a cancelaciones de términos opuestos. Haciendo que se pueda definir la siguiente igualdad para sumatorias telescópicas:
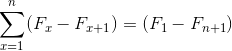
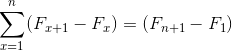
Su nombre proviene de la relación con la apariencia de un telescopio clásico, los cuales podían plegarse y desplegarse, cambiando notablemente su dimensión. De igual manera las sumatorias telescópicas, que en su naturaleza son infinitas, pueden resumirse en la expresión simplificada:
F1 – Fn+1
Índice del artículo
Al desarrollar la sumatoria de términos, resulta bastante obvia la eliminación de factores. Donde para cada uno de los casos, aparecerán elementos opuestos en la siguiente iteración.
Se tomará como ejemplo el primer caso, (Fx – Fx+1), ya que el proceso funciona de manera homóloga para (Fx+1–Fx).
Desarrollando los 3 primeros valores { 1 , 2 , 3 } se observa la tendencia de la simplificación
X1 (F1 – F1+1) = F1 – F2
X2 (F2 – F2+1) = F2 – F3
X3 (F3 – F3+1) = F3 – F4
Donde al expresar la sumatoria de los elementos descritos:
X1 + X2 + X3 = F1 – F2 + F2 – F3 + F3 – F4
Se observa que los términos F2 y F3 están descritos junto a sus opuestos, lo cual hace inevitable su simplificación. De igual manera se observa que los términos F1 y F4 se mantienen.
Si la suma fue efectuada desde x = 1 hasta x = 3, quiere decir que el elemento F4 corresponde al término genérico Fn+1.
Demostrándose así la igualdad:
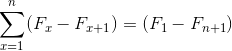
La finalidad de las sumatorias telescópicas es facilitar el trabajo, de manera que no resulte necesario desarrollar una cantidad infinita de términos, o simplificar alguna cadena de sumandos demasiado larga.
Para su resolución solo será necesario evaluar los términos F1 y Fn+1. Estas simples sustituciones componen el resultado final de la sumatoria.
La totalidad de los términos no será expresada, haciéndose necesaria únicamente para la demostración del resultado, pero no para el proceso normal de cálculo.
Lo importante es notar la convergencia de la serie numérica. En ocasiones el argumento de la sumatoria no estará expresado de forma telescópica. En estos casos es muy común la implementación de métodos alternativos de factorización.
El método de factorización característico en las sumatorias telescópicas, es el de fracciones simples. Este se da cuando una fracción original se descompone en una suma de varias fracciones, donde puede observarse el patrón telescópico (Fx – Fx+1) o (Fx+1 – Fx).
Para verificar la convergencia de las series numéricas, es muy común transformar expresiones racionales con el método de fracciones simples. La meta es modelar el argumento hasta darle la forma de una sumatoria telescópica.
Por ejemplo, la siguiente igualdad representa una descomposición en fracciones simples:
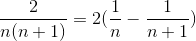
Al desarrollar la serie numérica y aplicar las propiedades correspondientes la expresión toma la siguiente forma:
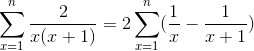
Donde se aprecia la forma telescópica (Fx – Fx+1).
El procedimiento es bastante intuitivo y consiste en encontrar los valores del numerador que, sin romper la igualdad, permitan separar los productos que se hallan en el denominador. Las ecuaciones que surgen en la determinación de estos valores, se plantean según comparaciones entre ambos lados de la igualdad.
Este procedimiento se observa paso a paso en el desarrollo del ejercicio 2.
Es bastante incierto poder definir el momento histórico en que se presentaron las sumatorias telescópicas. Sin embargo, su implementación comienza a verse en el siglo XVII, en los estudios de series numéricas realizados por Leibniz y Huygens.
Ambos matemáticos, al explorar las sumatorias de números triangulares, comienzan a notar tendencias en la convergencia de ciertas series de elementos sucesivos. Pero aún más interesante es el comienzo del modelado de estas expresiones, en elementos que no necesariamente se suceden.
De hecho, la expresión usada con anterioridad para referirnos a las fracciones simples:
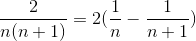
Fue presentada por Huygens y llamó de inmediato la atención de Leibniz. Quien con el tiempo pudo observar la convergencia al valor 2. Sin saberlo implementó el formato de sumatoria telescópica.
Defina a qué término converge la siguiente sumatoria:
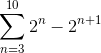
Al desarrollar manualmente la sumatoria se observa el siguiente patrón:
(23 – 24) + (24 – 25) + (25 – 26) . . . . (210 – 211)
Donde los factores desde 24 hasta 210 presentan partes positivas y negativas, haciendo evidente su cancelación. Luego los únicos factores que no se simplificarán serán el primero “23” y el último “211”.
De esta manera al implementar el criterio de sumatoria telescópica se obtiene:
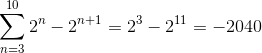
Transformar el argumento en una sumatoria de tipo telescópica y defina la convergencia de la serie:
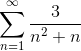
Tal como se indica en el enunciado, lo primero será realizar la descomposición en fracciones simples, para así replantear el argumento y expresarlo en forma telescópica.
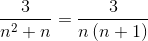
Se deben encontrar 2 fracciones cuyos denominadores sean respectivamente “n” y “n+1”, donde el método utilizado a continuación debe conseguir los valores del numerador que cumplen la igualdad.
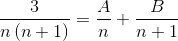
Se procede a definir los valores de A y B. Primeramente se efectúa suma de fracciones.
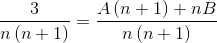
Luego, se simplifican los denominadores y se establece una ecuación lineal.
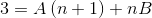
En el siguiente paso se opera la expresión de la derecha, hasta conseguir un patrón comparable con el “3” de la izquierda.
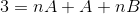
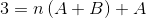
Para definir las ecuaciones a utilizar, se deben comparar los resultados de ambos lados de la igualdad. Es decir, no se observan valores de la variable n en el lado izquierdo, de esta forma A +B tendrá que ser igual a cero.
A + B = 0; A = -B
Por otra parte el valor constante A tendrá que ser igual al valor constante 3.
A = 3
Por lo tanto.
A = 3 y B = -3
Definidos ya los valores del numerador para las fracciones simples, se procede a replantear la sumatoria.
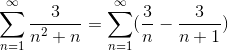
Donde ya se ha logrado conseguir la forma genérica de sumatoria telescópica. Se procede a desarrollar la serie telescópica.
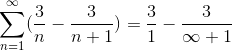
Donde al dividir entre un número muy grande el resultado se aproximará cada vez más a cero, observándose la convergencia de la serie al valor 3.
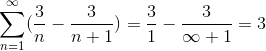
Este tipo de series no podrían ser resueltas de otro modo, debido a la infinita cantidad de iteraciones que definen al problema. Sin embargo, este método, junto a muchos otros enmarcan la rama de estudio de las series numéricas, cuyo objetivo es determinar los valores de convergencia o definir la divergencia de dichas series.
- Lecciones de cálculo infinitesimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
- Cálculo Integral: Sucesiones y Series de Funciones. Antonio Rivera Figueroa. Grupo Editorial Patria, 21 oct. 2014.
- A Course in Calculus and Real Analysis. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 jun. 2006.
- Infinite series. Tomlinson Fort. The Clarendon Press, 1930.
- Elements of the Theory of Infinite Processes. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorporated, 1923.
