Grado de un polinomio: cómo se determina, ejemplos y ejercicios
El grado de un polinomio en una variable viene dado por el término que tenga el exponente mayor, y si el polinomio tiene dos o más variables, entonces el grado se determina mediante la suma de los exponentes de cada término, siendo la suma mayor el grado del polinomio.
Veamos cómo determinar el grado del polinomio de una manera práctica.

Supongamos el polinomio P(x) = -5x + 8x3 + 7 – 4x2. Este polinomio es de una variable, en este caso se trata de la variable x. Este polinomio consta de varios términos, que son los siguientes:
-5x; 8x3; 7; – 4x2
Seleccionemos de entre los cuatro términos aquel cuyo exponente es mayor, este término es:
8x3
Y ahora ¿cuál es el exponente? La respuesta es 3. Por lo tanto P(x) es un polinomio de grado 3.
Si el polinomio en cuestión tiene más de una variable, entonces el grado puede ser:
-Absoluto
-En relación a una variable
El grado absoluto se encuentra como se explicó al comienzo: sumando los exponentes de cada término y seleccionando el mayor.
En cambio, el grado del polinomio respecto a una de las variables o letras, es el valor más grande del exponente que tenga dicha letra. El punto quedará más claro con los ejemplos y ejercicios resueltos de las siguientes secciones.
Índice del artículo
- 1 Ejemplos de grado de un polinomio
- 2 Procedimiento para trabajar con polinomios
- 3 Ejercicios resueltos
- 4 Referencias
Los polinomios pueden clasificarse por el grado, pudiendo ser de primer grado, segundo grado, tercer grado y así sucesivamente. Para el ejemplo de la figura 1, la energía es un monomio de primer grado para la masa.
También es importante observar que el número de términos que tiene un polinomio es igual al grado más 1. Así:
-Los polinomios de primer grado tienen 2 términos: a1x + ao
-El polinomio de segundo grado tiene 3 términos: a2x2 + a1x + ao
-Un polinomio de tercer grado posee 4 términos: a3x3 + a2x2 + a1x + ao
Y así sucesivamente. El lector atento habrá observado que los polinomios de los ejemplos anteriores están escritos en forma decreciente, es decir, colocando primero el término con el grado mayor.
En la siguiente tabla aparecen diversos polinomios, tanto de una como de varias variables y sus respectivos grados absolutos:
| Polinomio | Grado |
|---|---|
| 3x4+5x3-2x+3 | 4 |
| 7x3-2x2+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| x5-bx4+abx3+ab3x2 | 6 |
| 3x3y5 + 5x2y4 – 7xy2 + 6 | 8 |
Los dos últimos polinomios tienen más de una variable. De ellos se ha destacado en negrita el término que posee el mayor grado absoluto, para que el lector compruebe rápidamente el grado. Importante recordar que cuando la variable no tiene exponente escrito, se entiende que dicho exponente es igual a 1.
Por ejemplo en el término destacado ab3x2 hay tres variables, a saber: a, b y x. En dicho término, a está elevado a la 1, es decir:
a = a1
Por lo tanto ab3x2 = a1b3x2
Ya que el exponente de b es 3 y el de x es 2, se sigue de inmediato que el grado de este término es:
1+3+2 = 6
Y es el grado absoluto del polinomio, pues ningún otro de los términos posee un grado mayor.
Al trabajar con polinomios es importante prestar atención al grado del mismo, ya que en primer lugar y antes de realizar cualquier operación, es conveniente seguir estos pasos, en los cuales el grado brinda una información muy importante:
-Ordenar el polinomio de preferencia en sentido decreciente. De esta manera, el término con el grado mayor se encuentra a la izquierda y el de menor grado a la derecha.
-Reducir términos semejantes, un procedimiento que consiste en sumar algebraicamente todos los términos de igual variable y grado que se encuentren en la expresión.
-De ser preciso, los polinomios se completan, intercalando términos cuyo coeficiente sea 0, en caso de que falten términos con algún exponente.
Dado el polinomio P(x) = 6x2 – 5x4– 2x+3x+7+2x5 – 3x3 + x7 -12 se pide ordenarlo en forma decreciente, reducir los términos semejantes si los hay y completar los términos que falten de ser preciso.
Lo primero que se debe buscar es el término con el exponente mayor, que es el grado del polinomio, el cual resulta ser:
x7
Por lo tanto P(x) es de grado 7. Seguidamente se ordena el polinomio, comenzando con este término a la izquierda:
P(x) = x7 + 2x5 – 5x4 – 3x3 + 6x2 – 2x+3x+7 -12
Ahora se reducen los términos semejantes, que son los siguientes: – 2x y 3x por un lado. Y 7 y -12 por el otro. Para reducirlos se suman algebraicamente los coeficientes y se deja inalterada la variable (si la variable no aparece junto al coeficiente hay que recordar que x0 = 1):
-2x+3x = x
7 -12 = -5
Se sustituyen estos resultados en P(x):
P(x) = x7 +2x5 – 5x4 – 3x3 + 6x2 + x -5
Y finalmente se examina el polinomio a ver si falta algún exponente y en efecto, falta un término cuyo exponente sea 6, por lo tanto se completa con ceros así:
P(x) = x7 + 0x6 +2x5 – 5x4 – 3x3 + 6x2 + x – 5
Ahora se observa que el polinomio quedó con 8 términos, ya que como se dijo antes, el número de términos es igual al grado + 1.
Con los polinomios se pueden realizar operaciones de suma y resta, en las cuales solamente se suman o restan los términos semejantes, que son los que tienen la misma variable y el mismo grado. Si no hay términos semejantes, la suma o la resta se deja simplemente indicada.
Una vez realizada la suma o la resta, esta última siendo la suma del opuesto, el grado del polinomio resultante siempre es igual o menor que el grado del polinomio sumando de mayor grado.
Encontrar la siguiente suma y determinar su grado absoluto:
a3– 8ax2 + x3 + 5a2x – 6ax2 – x3 + 3a3 – 5a2x – x3 + a3+ 14ax2 – x3
Solución
Se trata de un polinomio de dos variables, por lo que es conveniente ir reduciendo los términos semejantes:
a3– 8ax2 + x3 + 5a2x – 6ax2 – x3 + 3a3 – 5a2x – x3 + a3+ 14ax2 – x3 =
= a3 + 3a3 + a3 – 8ax2 – 6ax2+ 14ax2 +5a2x – 5a2x+ x3– x3– x3– x3 =
= 5a3 – 2x3
Ambos términos son de grado 3 en cada variable. Por lo tanto el grado absoluto del polinomio es 3.
Expresar como polinomio el área de la siguiente figura geométrica plana (figura 2 izquierda). ¿Cuál es el grado de polinomio resultante?
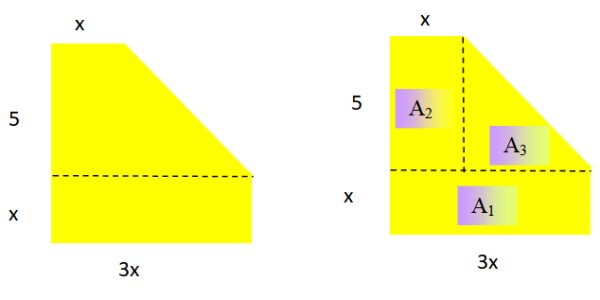
Solución
Al tratarse de un área, el polinomio resultante debe ser de grado 2 en la variable x. Para determinar una expresión adecuada para el área, se descompone la figura en áreas conocidas:
El área de un rectángulo y de un triángulo son respectivamente: base x altura y base x altura /2
A1 = x . 3x = 3x2; A2 = 5 . x = 5x; A3 = 5 . (2x /2) = 5x
Nota: la base del triángulo es 3x – x = 2x y su altura es 5.
Ahora se suman las tres expresiones obtenidas, con ello se tiene el área de la figura en función de x:
3x2 + 5x + 5x = 3x2 + 10x
- Baldor, A. 1974. Algebra Elemental. Cultural Venezolana S.A.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Wikilibros. Polinomios. Recuperado de: es. wikibooks.org.
- Wikipedia. Grado (polinomio). Recuperado de: es.wikipedia.org.
- Zill, D. 1984. Álgebra y Trigonometría. Mac Graw Hill.
