Álgebra vectorial: qué es, fundamentos, magnitudes, vectores

¿Qué es el álgebra vectorial?
El álgebra vectorial es una rama de las matemáticas encargada de estudiar sistemas de ecuaciones lineales, vectores, matrices, espacios vectoriales y sus transformaciones lineales. Se relaciona con áreas como ingeniería, resolución de ecuaciones diferenciales, análisis funcional, investigación de operaciones, gráficas computacionales, entre otras.
Otra de las áreas que ha adoptado el álgebra lineal es la física, ya que a través de esta se ha logrado desarrollar el estudio de fenómenos físicos, describiéndolos mediante el uso de vectores. Esto ha hecho posible una mejor comprensión del universo.
Fundamentos
El álgebra vectorial se originó del estudio de los cuaterniones (extensión de los números reales) 1, i, j, y k, así como también de la geometría cartesiana promovida por Gibbs y Heaviside, quienes se dieron cuenta de que los vectores servirían de instrumento para representar varios fenómenos físicos.
El álgebra vectorial es estudiada a través de tres fundamentos:
Geométricamente
Los vectores son representados por rectas que tienen una orientación, y las operaciones como suma, resta y multiplicación por números reales son definidas a través de métodos geométricos.
Analíticamente
La descripción de los vectores y sus operaciones es realizada con números, llamados componentes. Este tipo de descripción es resultado de una representación geométrica porque se utiliza un sistema de coordenadas.
Axiomáticamente
Se hace una descripción de los vectores, independientemente del sistema de coordenadas o de cualquier tipo de representación geométrica.
El estudio de figuras en el espacio se hace a través de su representación en un sistema de referencia, que puede ser en una o más dimensiones. Entre los principales sistemas se encuentran:
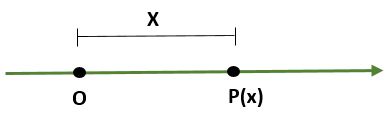
- Sistema unidimensional, que se trata de una recta donde un punto (O) representa el origen y otro punto (P) determina la escala (longitud) y el sentido de esta:
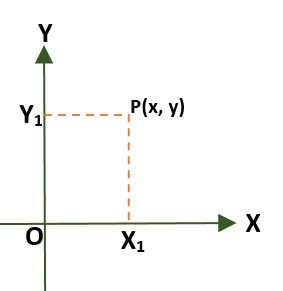
- Sistema de coordenadas rectangulares (bidimensional), que está compuesto por dos rectas perpendiculares llamadas eje x y eje y, que pasan por un punto (O) origen; de esa forma el plano queda divido en cuatro regiones llamadas cuadrantes. En este caso un punto (P) en el plano es dado por las distancias que existen entre los ejes y P.
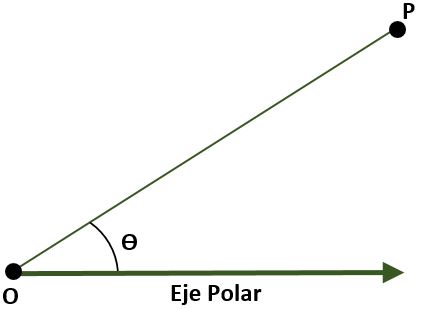
- Sistema de coordenadas polares (bidimensional). En este caso el sistema es compuesto por un punto O (origen) que es llamado polo y una semirrecta con origen en O llamada eje polar. En este caso el punto P del plano, con referencia al polo y al eje polar, es dado por el ángulo (Ɵ), que se forma por la distancia que existe entre el origen y el punto P.
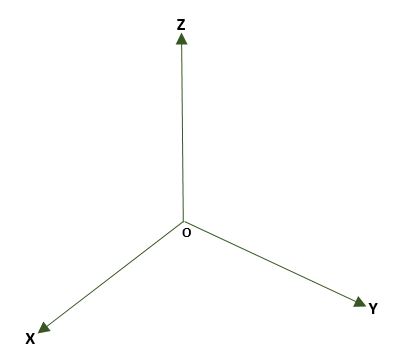
- Sistema tridimensional rectangular, formado por tres rectas perpendiculares (x, y, z) que tienen como origen un punto O en el espacio. Se forman tres planos coordenados: xy, xz y yz; el espacio quedará dividido en ocho regiones llamadas octantes. La referencia de un punto P del espacio es dada por las distancias que existen entre los planos y P.
Magnitudes
Una magnitud es una cantidad física que puede ser contada o medida a través de un valor numérico, como en el caso de algunos fenómenos físicos; sin embargo, muchas veces es necesario poder describir esos fenómenos con otros factores que no sean numéricos. Por eso las magnitudes son clasificadas en dos tipos:
Magnitud escalar
Son aquellas cantidades que se definen y representan de forma numérica; es decir, por un módulo junto con una unidad de medida. Por ejemplo:
a) Tiempo: 5 segundos.
b) Masa: 10 kg.
c) Volumen: 40 ml.
d) Temperatura: 40 ºC.
Magnitud vectorial
Son aquellas cantidades que son definidas y representadas por un módulo junto con una unidad, así como también por un sentido y dirección. Por ejemplo:
a) Velocidad: (5ȋ – 3ĵ) m/s.
b) Aceleración: 13 m /s2; S 45º E.
c) Fuerza: 280 N, 120º.
d) Peso: -40 ĵ kg-f.
Las magnitudes vectoriales son representadas gráficamente por vectores.
¿Qué son los vectores?
Los vectores son representaciones gráficas de una magnitud vectorial; es decir, son segmentos de recta en los que su extremo final es la punta de una flecha.
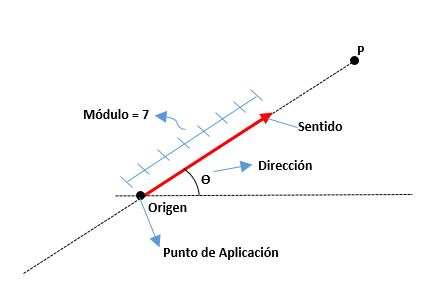
Estos son determinados por su módulo o longitud del segmento, su sentido que es indicado por la punta de su flecha y su dirección de acuerdo con la recta a la que pertenezca. El origen de un vector es también conocido como el punto de aplicación.
Los elementos de un vector son los siguientes:
Módulo
Es la distancia que hay desde el origen hasta el extremo de un vector, representada por un número real junto con una unidad. Por ejemplo:
|OM| = |A| = A = 6 cm
Dirección
Es la medida del ángulo que existe entre el eje x (a partir del positivo) y el vector, así como también se utilizan los puntos cardinales (norte, sur, este y oeste).
Sentido
Es dado por la punta de flecha ubicada en el extremo del vector, indicando hacia dónde se dirige este.
Clasificación de los vectores
Generalmente, los vectores son clasificados como:
Vector fijo
Es aquel cuyo punto de aplicación (origen) es fijo; es decir, que se mantiene ligado a un punto del espacio, por lo que no puede desplazarse en este.
Vector libre
Puede moverse libremente en el espacio porque su origen se traslada a cualquier punto sin cambiar su módulo, sentido o dirección.
Vector deslizante
Es aquel que puede trasladar su origen a lo largo de su línea de acción sin cambiar su módulo, sentido o dirección.
Propiedades de los vectores
Entre las principales propiedades de los vectores se encuentran las siguientes:
Vectores equipolentes
Son aquellos vectores libres que tienen igual módulo, dirección (o estas son paralelas) y sentido que un vector deslizante o un vector fijo.
Vectores equivalentes
Ocurre cuando dos vectores tienen la misma dirección (o son paralelas), el mismo sentido, y a pesar de tener diferentes módulos y puntos de aplicación, estos provocan efectos iguales.
Igualdad de vectores
Estos tienen igual módulo, dirección y sentido, aun cuando sus puntos de partida son diferentes, lo que permite que un vector paralelo se traslade a sí mismo sin afectarlo.
Vectores opuestos
Son aquellos que tienen el mismo módulo y dirección, pero su sentido es opuesto.
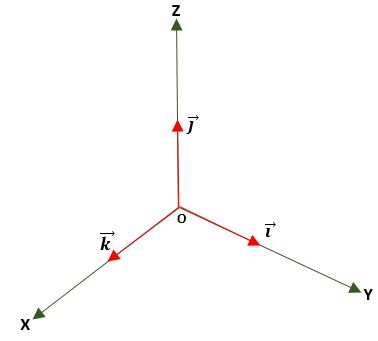
Vector unitario
Es aquel en el que el módulo es igual a la unidad (1). Este se obtiene al dividir el vector por su módulo y es utilizado para determinar la dirección y sentido de un vector, bien sea en el plano o en el espacio, utilizando los vectores base o unitarios normalizados, que son:
Vector nulo
Es aquel cuyo módulo es igual a 0; es decir, su punto de origen y extremo coinciden en un mismo punto.
Componentes de un vector
Las componentes de un vector son aquellos valores de las proyecciones del vector sobre los ejes del sistema de referencia; dependiendo de la descomposición del vector, que puede ser en ejes de dos o tres dimensiones, se obtendrán dos o tres componentes, respectivamente.
Las componentes de un vector son números reales, que pueden ser positivos, negativos o incluso cero (0).
De esa forma, si se tiene un vector Ā, con origen en un sistema de coordenadas rectangulares en el plano xy (bidimensional), la proyección sobre el eje x es Āx y la proyección sobre el eje y es Āy. Así, el vector se expresará como la suma de sus vectores componentes.
Ejemplos
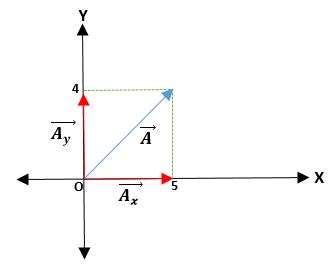
Primero ejemplo
Se tiene un vector Ā que parte del origen y las coordenadas de sus extremos son dadas. Así, el vector Ā = (Āx; Ay) = (4; 5) cm.
Si el vector Ā actúa en el origen de un sistema de coordenadas triangulares tridimensionales (en el espacio) x, y, z, hasta otro punto (P), las proyecciones sobre sus ejes serán Āx, Āy y Āz; así, el vector se expresará como la suma de sus tres vectores componentes.
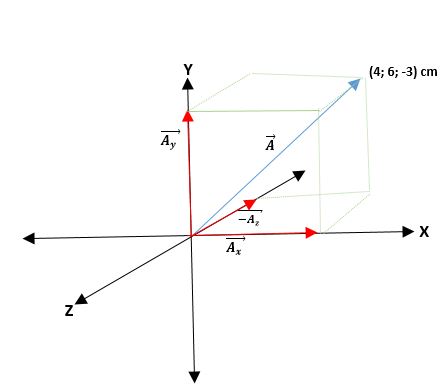
Segundo ejemplo
Se tiene un vector Ā que parte del origen y las coordenadas de sus extremos son dadas. Así, el vector Ā = (Ax; Ay; Az) = (4; 6; -3) cm.
Los vectores que tienen sus coordenadas rectangulares pueden expresarse en función de sus vectores base. Para eso solo se debe multiplicar cada coordenada por su respectivo vector unitario, de tal forma que para el plano y el espacio serán las siguientes:
Para el plano: Ā=Axi + Ayj.
Para el espacio: Ā=Axi + Ayj+Azk.
Operaciones con vectores
Existen muchas magnitudes que tienen módulo, sentido y dirección, como aceleración, velocidad, desplazamiento, fuerza, entre otros.
Estas son aplicadas en diversas áreas de las ciencias, y para aplicarlas se hace necesario en algunos casos realizar operaciones como suma, resta, multiplicación y división de vectores y escalares.
Suma y resta de vectores
La suma y resta de vectores es considerada una sola operación algebraica porque la resta puede ser escrita como una suma; por ejemplo, la resta de los vectores Ā y Ē puede expresarse como:
Ā – Ē = Ā + (-Ē)
Existen diferentes métodos para realizar la suma y resta de vectores: pueden ser gráficos o analíticos.
Métodos gráficos
Utilizados cuando un vector posee módulo, sentido y dirección. Para ello se trazan líneas que forman una figura que posteriormente ayudan a determinar la resultante. Entre los más conocidos destacan los siguientes:
Método del paralelogramo
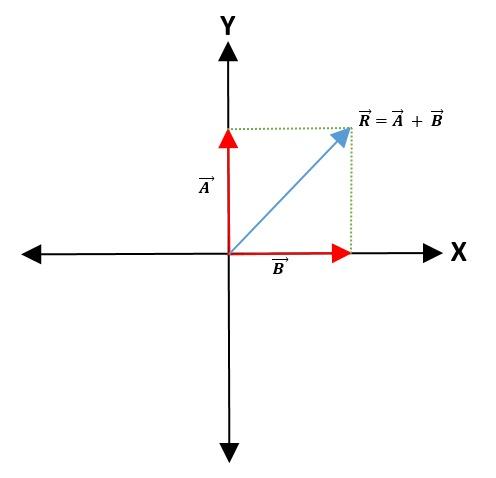
Para hacer la suma o resta de dos vectores se elige un punto en común sobre el eje de coordenadas —que representará el punto de origen de los vectores—, manteniendo su módulo, sentido y direcci.
Entonces se trazan líneas paralelas a los vectores para formar un paralelogramo. El vector resultante es la diagonal que sale desde el punto de origen de ambos vectores hasta el vértice del paralelogramo:
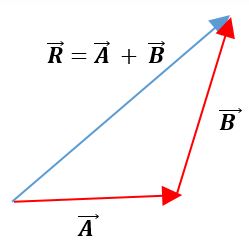
Método del triángulo
En este método los vectores se colocan uno a continuación el otro, manteniendo sus módulos, sentidos y direcciones. El vector resultante será la unión del origen del primer vector con el extremo del segundo vector:
Métodos analíticos
Se pueden sumar o restar dos o más vectores a través de un método geométrico o vectorial:
Método geométrico
Cuando dos vectores forman un triángulo o paralelogramo, el m[odulo y la dirección del vector resultante puede ser determinado usando la leyes del seno y coseno. Así, el módulo del vector resultante, aplicando la ley del coseno y por el método del triángulo, es dado por:
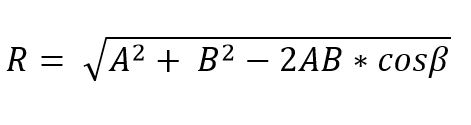
En esta fórmula β es el ángulo opuesto al lado R, y este es igual a 180º – Ɵ.
En cambio, por el método del paralelogramo el módulo del vector resultante es:
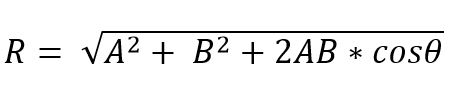
La dirección del vector resultante es dada por el ángulo (α), que forma la resultante con uno de los vectores.
Por la ley del seno, la suma o resta de vectores puede hacerse también por el método del triángulo o paralelogramo, sabiendo que en todo triángulo los lados son proporcionales a los senos de los ángulos apuestos:
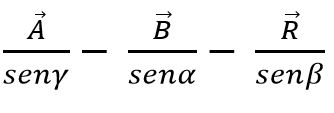
Método vectorial
Este se puede hacer de dos formas: en función de sus coordenadas rectangulares o de sus vectores bases.
Se puede hacer trasladando los vectores que se van a sumar o restar hacia el origen de coordenadas, y luego se descomponen en sus componentes rectangulares todas las proyecciones en cada uno de los ejes para el plano (x, y) o el espacio (x, y, z); por último, se suman sus componentes algebráicamente. Entonces, para el plano es:
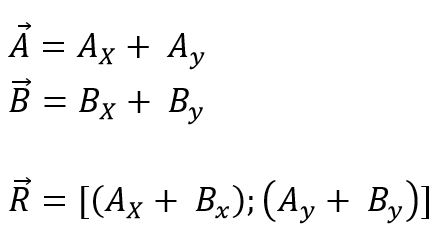
El módulo del vector resultante es:
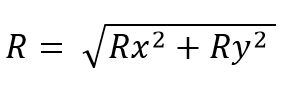
Mientras que para el espacio es:
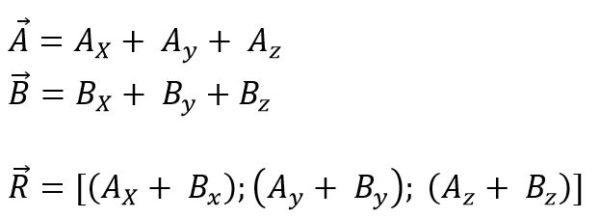
El módulo del vector resultante es:
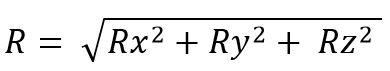
Cuando se realizan sumas vectoriales se aplican varias propiedades, que son:
- Propiedad asociativa: la resultante no cambia al sumar dos vectores primero, y después sumarle un tercer vector.
- Propiedad conmutativa: el orden de los vectores no altera la resultante.
- Propiedad distributiva vectorial: si se multiplica un escalar por la suma de dos vectores, es igual a la multiplicación del escalar por cada vector.
- Propiedad distributiva escalar: si se multiplica un vector por la suma de dos escalares, es igual a la multiplicación del vector por cada escalar.
Multiplicación de vectores
La multiplicación o producto de vectores pudiera realizarse como la suma o resta, pero al hacerlo de esa forma pierde el significado físico y casi nunca se encuentra dentro de las aplicaciones. Por eso, generalmente los tipos de productos más utilizados son el producto escalar y vectorial.
Producto escalar
Es conocido también como producto punto de dos vectores. Cuando se multiplican los módulos de dos vectores por el coseno del ángulo menor que se forma entre estos se obtiene un escalar. Para expresar un producto escalar entre dos vectores se coloca un punto entre estos, y este puede definirse como:
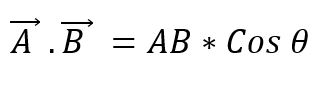
El valor del ángulo que existe entre los dos vectores va a depender de si estos son paralelos o perpendiculares; así, se tiene que:
- Si los vectores son paralelos y tienen el mismo sentido, coseno 0º = 1.
- Si los vectores son paralelos y tienen sentidos opuestos, coseno 180º = -1.
- Si los vectores son perpendiculares, coseno 90º = 0.
Ese ángulo también puede ser calculado sabiendo que:

El producto escalar tiene las siguientes propiedades:
- Propiedad conmutativa: el orden de los vectores no altera el escalar.
- Propiedad distributiva: si se multiplica un escalar por la suma de dos vectores, es igual a la multiplicación del escalar por cada vector.
Producto vectorial
La multiplicación vectorial, o producto cruz de dos vectores A y B, dará como resultado un nuevo vector C y se expresa utilizando una cruz entre los vectores:
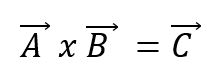
El nuevo vector tendrá sus propias características. De esa manera:
- La dirección: este nuevo vector será perpendicular al plano, que es determinado por los vectores originales.
- El sentido: este se determina con la regla de la mano derecha, donde se gira el vector A hacia el B señalando el sentido de la rotación con los dedos, y con el pulgar se marca el sentido del vector.
- El módulo: es determinado por la multiplicación de los módulos de los vectores AxB, por el seno del ángulo menor que existe entre estos vectores. Se expresa:
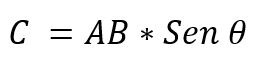
El valor del ángulo que existe entre los dos vectores va a depender de si estos son paralelos o perpendiculares. Entonces, es posible afirmar lo siguiente:
- Si los vectores son paralelos y tienen el mismo sentido, seno 0º = 0.
- Si los vectores son paralelos y tienen sentidos opuestos, seno 180º = 0.
- Si los vectores son perpendiculares, seno 90º = 1.
Cuando un producto vectorial es expresado en función de sus vectores bases, se tiene que:
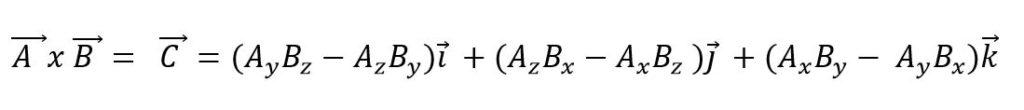
El producto escalar tiene las siguientes propiedades:
- No es conmutativo: el orden de los vectores altera el escalar.
- Propiedad distributiva: si se multiplica un escalar por la suma de dos vectores, es igual a la multiplicación del escalar por cada vector.
