Diámetro: símbolos y fórmulas, cómo sacarlo, circunferencia
El diámetro es la línea recta que pasa por el centro de una curva plana cerrada o bien una figura en dos o tres dimensiones y que además une sus puntos opuestos. Usualmente se trata de una circunferencia (una curva plana), un círculo (una figura plana), una esfera o un cilindro circular recto (objetos tridimensionales).
Pese a que circunferencia y círculo suelen tomarse como sinónimos, existe diferencia entre ambos términos. La circunferencia es la curva cerrada que encierra al círculo, que cumple con la condición de que la distancia entre cualquiera de sus puntos y el centro es la misma. Esta distancia no es otra que el radio de la circunferencia. En cambio, el círculo es una figura plana limitada por la circunferencia.

En caso de circunferencia, círculo y esfera, el diámetro es un segmento recto que contiene al menos tres puntos: el centro más dos puntos del borde de la circunferencia o círculo, o la superficie de la esfera.
Y en cuanto al cilindro circular recto, el diámetro se refiere a la sección transversal, que junto con la altura, son sus dos parámetros característicos.
El diámetro de la circunferencia y el círculo, simbolizado por ø o simplemente la letra “D” o “d”, está relacionado con su perímetro, contorno o longitud, que se denota con la letra L:
L= π.D = π. ø
Siempre que se tenga una circunferencia, el cociente entre su longitud y su diámetro es el número irracional π = 3.14159…, de esta forma:
π = L/D
Índice del artículo
- 1 ¿Cómo sacar el diámetro?
- 2 Diámetro de una circunferencia
- 3 ¿Cuántos diámetros tiene una circunferencia?
- 4 Referencias
Cuando se dispone del dibujo de la circunferencia o del círculo, o directamente el objeto circular, como una moneda o un anillo por ejemplo, es muy fácil sacar el diámetro con una regla. Simplemente hay que asegurarse de que el borde de la regla toque al mismo tiempo dos puntos de la circunferencia y el centro de la misma.
Una calibre, vernier o pie de rey es muy adecuado para medir diámetros externos e internos en monedas, aros, anillos, tuercas, tubos y más.

Si en vez del objeto o su dibujo se tienen datos como el radio R, entonces multiplicando por 2 se tiene el diámetro. Y si se conoce la longitud o perímetro de la circunferencia también se puede conocer el diámetro, mediante despeje:
D = 2.R
D = L / π
Otra manera de sacar el diámetro es conociendo el área del círculo, la superficie esférica, la sección transversal del cilindro, el área curvada de este o los volúmenes de la esfera o el cilindro. Todo depende de qué figura geométrica se trate. Por ejemplo, el diámetro está involucrado en las siguientes áreas y volúmenes:
-Área del círculo: π.(D/2)2
-Área de la superficie esférica: 4π.(D/2)2
-Volumen de la esfera: (4/3) π.(D/2)3
-Volumen del cilindro circular recto: π.(D/2)2.H (H es la altura del cilindro)
El círculo es una figura plana de ancho constante, ya que por donde quiera que se le mire, el ancho es el diámetro D. Sin embargo, existen otras figuras quizá menos conocidas cuyo ancho también es constante.
Primero veamos lo que se entiende por ancho de una figura: es la distancia entre dos rectas paralelas –rectas de soporte-, que a su vez son perpendiculares a la dirección dada y que aprisionan la figura, tal como lo muestra en la imagen izquierda:
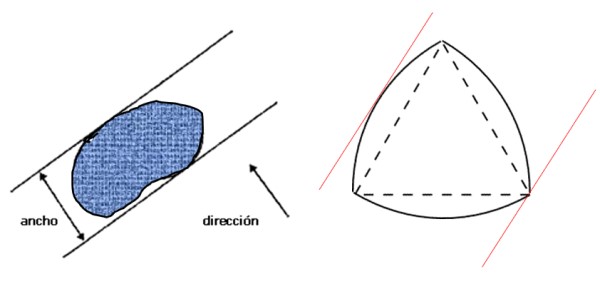
Seguidamente a la derecha está el triángulo de Reuleaux, que es una figura de ancho constante y que cumple con la condición especificada en la figura izquierda. Si el ancho de la figura es D, su perímetro viene dado por el teorema de Barbier:
L = π.D
Las alcantarillas de la ciudad de San Francisco en California tienen forma de triángulo de Reuleaux, nombrado así por el ingeniero alemán Franz Reuleaux (1829 – 1905). De esta manera las tapas no pueden caerse por el agujero y se gasta menos material en fabricarlas, pues su área es menor que la del círculo:
A = ( 1- √3).πD2 = 0.705.D2
Mientras que para un círculo:
A = π.(D/2)2 = (π/4)D2= 0.785.D2
Pero este triángulo no es la única figura de ancho constante. Se pueden construir los llamados polígonos de Reuleaux con otros polígonos que tengan número de lados impar.

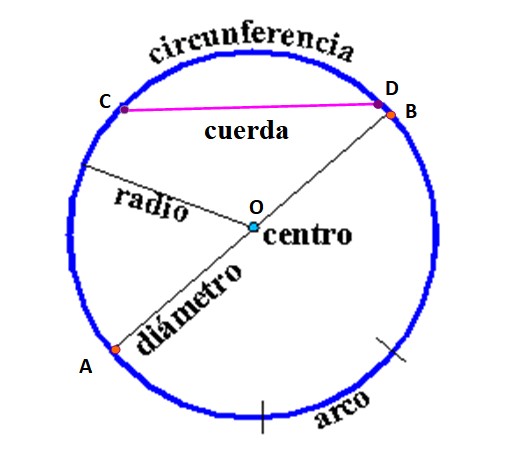
En la próxima figura se encuentran los elementos de la circunferencia, definidos del siguiente modo:
Cuerda: segmento de recta que une dos puntos de la circunferencia. En la figura está la cuerda que une los puntos C y D, pero se pueden trazar infinitas cuerdas que unan cualquier pareja de puntos de la circunferencia.
Diámetro: es la cuerda que pasa por el centro, uniendo dos puntos de la circunferencia con el centro O. Es la cuerda de más larga de un circunferencia, por ese motivo se la llama “cuerda mayor”.
Radio: segmento de recta que une al centro con cualquier punto de la circunferencia. Su valor, al igual que el de diámetro, es constante.
Circunferencia: es el conjunto de todos los puntos que equidistan de O.
Arco: se define como un segmento de circunferencia delimitado por dos radios (no dibujados en la figura).
El rectángulo mostrado mide 10 pulgadas de altura, que al enrollarlo forma un cilindro circular recto cuyo diámetro es de 5 pulgadas. Responder las siguientes preguntas:
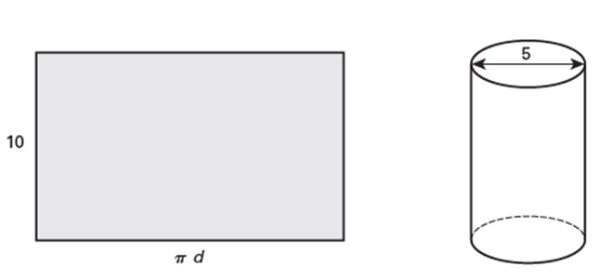
a) ¿Cuál es el contorno del tubo?
b) Encuentre el área del rectángulo
c) Calcule el área de la sección transversal del cilindro.
Solución a
El contorno del tubo es L = π.D = 5π plg = 15.71 plg.
Solución b
El área del rectángulo es base x altura, siendo la base L ya calculada y la altura es de 10 plg según el enunciado, por lo tanto:
A = 15.71 plg x 10 plg = 157.1 plg2.
Solución c
Por último, el área pedida se calcula así:
A = π.(D/2)2 = (π/4)D2 = (π/4) x (5 plg)2= 19.63 plg2.
Calcular el área sombreada de la figura 5a. El cuadrado tiene lado L.
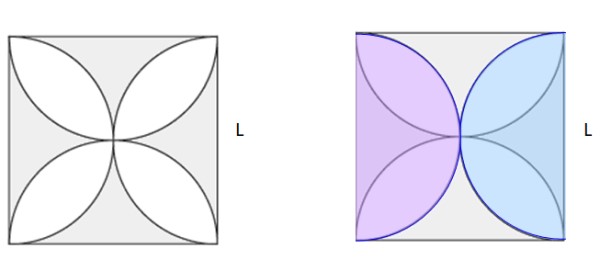
Solución
En la figura 5b se han dibujado dos semicírculos idénticos de tamaño en colores rosa y azul, superpuestos a la figura original. Entre ambos hacen un círculo completo. Si se calcula el área del cuadrado y se le resta el área del círculo, hace el área sombreada de la figura 5b. Y fijándose bien, resulta que es la mitad del área sombreada en 5a.
-Cuadrado de área: L2
-Diámetro del semicírculo: L
-Área del círculo: π.(L/2)2= (π/4)L2
-Diferencia de áreas = mitad del área sombreada =
L2 – (π/4)L2 =[(4 – π)/4] L2=0.2146 L2
-Área sombreada = 2 x 0.2146 L2= 0.4292L2
Se pueden trazar infinitos diámetros en una circunferencia, y cualquiera de ellos mide lo mismo.
- Antonio. Triángulos de Reuleaux y otras curvas de ancho constante. Recobrado de: divulgadores.com.
- Baldor, A. 2002. Geometría Plana y del Espacio y Trigonometría. Grupo Patria Cultural.
- Jiménez, R. Matemáticas II. Geometría y Trigonometría. 2da. Edición. Pearson.
- Wikipedia. Triángulo de Reuleaux. Recobrado de: es.wikipedia.org.
- Wolfram MathWorld. Diameter. Recuperado de: mathworld.wolfram.com.
