Raíz cuadrada de 3 (solución y explicación fácil)

La raíz cuadrada de 3 es 1,73205080756887.

Se puede expresar:

√3=1,73205080756887

Para conocer cuál es la raíz cuadrada de 3, es importante conocer la definición de la raíz cuadrada de un número. Dado un número positivo “a”, la raíz cuadrada de “a”, denotada por √a, es un número positivo “b” tal que cuando “b” se multiplica por el mismo, el resultado es “a”.

La definición matemática dice: √a=b si, y solo si, b²=b*b=a. Por lo tanto, para conocer cuál es la raíz cuadrada de 3, es decir, el valor de √3, se debe encontrar un número “b” tal que b²=b*b=√3.

Además, √3 es un número irracional, con lo cual este consta de una cantidad infinita no periódica de decimales. Por esta razón, es complicado calcular la raíz cuadrada de 3 manualmente.

Raíz cuadrada de 3

Si se utiliza una calculadora se puede aprecia que la raíz cuadrada de 3 es 1,73205080756887…

Ahora, se podría intentar manualmente aproximar este número de la siguiente forma:

-1*1=1 y 2*2=4, esto dice que la raíz cuadrada de 3 es un número entre 1 y 2.

-1,7*1,7=2,89 y 1,8*1,8=3,24, por lo tanto, la primera cifra decimal es 7.

-1,73*1,73=2,99 y 1,74*1,74=3,02, así la segunda cifra decimal es 3.

-1,732*1,732=2,99 y 1,733*1,733=3,003, por lo tanto, la tercera cifra decimal es 2.

Y así sucesivamente se puede continuar. Esta es una forma manual de calcular la raíz cuadrada de 3.

También existen otras técnicas mucho más avanzadas, como por ejemplo el método de Newton-Raphson, el cual es un método numérico para calcular aproximaciones.

¿Dónde podemos encontrar al número √3?

Por lo complicado del número, podría pensarse que no aparece en objetos cotidianos pero esto es falso. Si se tiene un cubo (caja cuadrada), tal que la longitud de sus lados sea 1, entonces las diagonales del cubo tendrán una medida de √3.

Para comprobar esto se utiliza el Teorema de Pitágoras que dice: dado un triángulo rectángulo, la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos (c²=a²+b²).

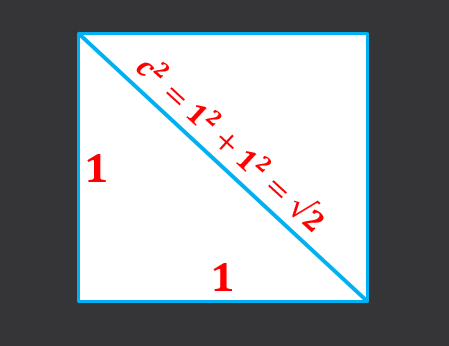
Al tener un cubo de lado 1, se tiene que la diagonal del cuadrado de su base es igual a la suma de los cuadrados de los catetos, esto es, c²=1²+1²=2, por lo tanto, la diagonal de la base mide √2.

Ahora, para calcular la diagonal del cubo se puede observar la siguiente figura.

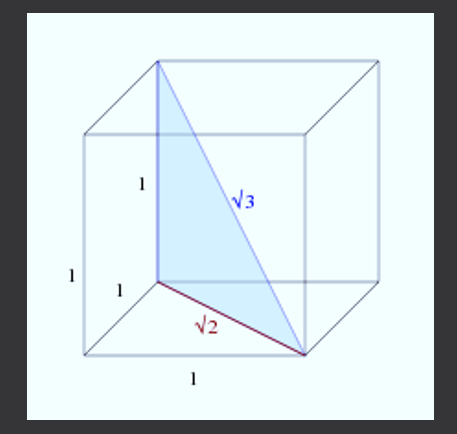
El nuevo triángulo rectángulo tiene catetos de longitudes 1 y √2, por lo tanto, al usar el teorema de Pitágoras para calcular la longitud de su diagonal se obtiene: C²=1²+(√2)²=1+2=3, es decir, C=√3.

Así, la longitud de la diagonal de un cubo de lado 1 es igual a √3.

√3 un número irracional

Al comienzo se dijo que √3 es un número irracional. Para comprobar esto, se supone por el absurdo que es un número racional, con lo cual existen dos números “a” y “b”, primos relativos, tales que a/b=√3.

Al elevar al cuadrado la última igualdad y despejar “a²”, se obtiene la siguiente ecuación: a²=3*b². Esto dice que “a²” es múltiplo de 3, con lo cual se concluye que “a” es múltiplo de 3.

Al ser “a” múltiplo de 3, existen un entero “k” tal que a=3*k. Por lo tanto, al reemplazar en la segunda ecuación se obtiene: (3*k)²=9*k²=3*b², lo que es lo mismo que b²=3*k².

Al igual que antes, esta última igualdad lleva a la conclusión de que “b” es múltiplo de 3.

En conclusión, “a” y “b” son ambos múltiplos de 3, lo cual es una contradicción, pues al principio se supuso que eran primos relativos.

Por lo tanto, √3 es un número irracional.