Teorema fundamental de la aritmética: demostración, aplicaciones, ejercicios

El teorema fundamental de la aritmética afirma que cualquier número natural mayor que 1 se puede descomponer como un producto de números primos -pudiendo repetirse algunos- y esta forma es única para dicho número, aunque el orden de los factores pueda ser diferente.

Recordemos que un número primo p es aquel que solo admite como divisores positivos a si mismo y al 1. Los siguientes números son primos: 2, 3, 5, 7, 11, 13 y así sucesivamente, puesto que hay infinitos. El número 1 no se considera primo, por tener un único divisor.

Por su parte, a los números que no cumplen lo anterior se les denomina números compuestos, como 4, 6, 8, 9, 10, 12, 14… Tomemos el número 10 por ejemplo y de inmediato vemos que se puede descomponer como producto de 2 y 5:

10 = 2 × 5

Tanto el 2 como el 5 son, efectivamente, números primos. El teorema afirma que esto es posible para cualquier número n:

Donde p₁, p₂, p₃… p_r son números primos y k₁, k₂, k₃,… k_r son números naturales. De forma que los números primos actúan como los ladrillos a partir de los cuales, mediante la multiplicación, se construyen los números naturales.

Índice del artículo

• 1 Demostración del teorema fundamental de la aritmética
  • 1.1 Unicidad de la descomposición en factores primos
• 2 Aplicaciones
  • 2.1 Los números primos en la naturaleza
  • 2.2 Los números primos y las compras online
• 3 Ejercicios resueltos
  • 3.1 – Ejercicio 1
  • 3.2 – Ejercicio 2
• 4 Referencias

Demostración del teorema fundamental de la aritmética

Se comienza demostrando que todo número se puede descomponer en factores primos. Sea un número natural n > 1, primo o compuesto.

Por ejemplo si n = 2, se puede expresar como: 2 = 1 × 2, que es primo. De igual forma se procede con los siguientes números:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Seguimos así, descomponiendo todos los números naturales hasta llegar al número n -1. Veamos si podemos hacerlo con el número que sigue: n.

Si n es primo, lo podemos descomponer como n = 1× n, pero supongamos que n es compuesto y tiene un divisor d, lógicamente menor que n:

1 d n.

Si n/d = p₁, con p₁ un número primo, entonces n se escribe como:

n = p₁.d

Si d es primo ya no hay más que hacer, pero si no lo es, existe un número n₂ que es divisor de d y menor que este: n₂ d, por lo que d podrá escribirse como el producto de n₂ por otro número primo p₂:

d = p₂ n₂

Que al sustituir en el número original n daría:

n = p₁ .p₂ .n₂

Ahora supongamos que n₂tampoco es un número primo y lo escribimos como el producto de un número primo p₃, por un divisor suyo n₃, tal que n₃ n₂ n₁ n:

n₂ = p₃.n₃ → n = p₁ p₂ p₃.n₃

 Repetimos este procedimiento un número finito de veces hasta obtener:

n = p₁.p₂.p₃ …p_r

Esto significa que sí es posible descomponer todos los números enteros desde el 2 hasta el número n, como un producto de números primos.

Unicidad de la descomposición en factores primos

Verifiquemos ahora que salvo el orden de los factores, esta descomposición es única. Supongamos que n se puede escribir de dos formas:

n = p₁.p₂.p₃ …p_r = q_1.q₂.q₃…..q_s  (con r ≤ s)

Desde luego q₁, q₂, q₃… son números primos también. Como p₁ divide a (q_1.q₂.q₃…..q_s) entonces p₁ es igual a alguno de los “q”, no importa a cuál, así que podemos decir que p₁ = q₁. Dividimos n entre p₁ y obtenemos:

p₂.p₃ …p_r =_.q₂.q₃…..q_s

Repetimos el procedimiento hasta dividir todo entre p_r, entonces obtenemos:

1 = q_r+1 … q_s

Pero no es posible llegar a q_r+1 … q_s = 1 cuando r s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Aplicaciones

Como hemos dicho antes, los números primos representan si se quiere, los átomos de los números, sus componentes básicos. Así que el teorema fundamental de la aritmética tiene numerosas aplicaciones, la más obvia: podemos trabajar más fácilmente con números grandes si los expresamos como el producto de números más pequeños.

De igual forma podemos hallar el máximo común múltiplo (m.c.m.) y el máximo común divisor (M.C.D.), un procedimiento que nos ayuda a hacer sumas de fracciones con más facilidad, encontrar raíces de números grandes, o bien operar con radicales, racionalizar y resolver problemas de aplicación de índole muy diversa.

Además los números primos son sumamente enigmáticos. No se reconoce todavía un patrón en ellos y no es posible saber cuál será el siguiente. El mayor hasta los momentos fue hallado mediante computadoras y tiene 24.862.048dígitos, aunque los nuevos números primos aparecen con menos frecuencia cada vez.

Los números primos en la naturaleza

Las cigarras, cicádidos o chicharras que viven en el noreste de los Estados Unidos emergen en ciclos de 13 o 17 años. Ambos son números primos.

De esta forma las chicharras evitan coincidir con predadores o competidores que tienen otros períodos de nacimiento, ni tampoco las diversas variedades de chicharra compiten entre sí, ya que no coinciden durante el mismo año.

Los números primos y las compras online

Los números primos se utilizan en criptografía para mantener en secreto los detalles de las tarjetas de crédito al realizar compras por Internet. De esta manera los datos que del comprador llegan precisamente a la tienda sin perderse o caer en manos de personas inescrupulosas.

¿Cómo? Los datos de las tarjetas son codificados en un número N que puede expresarse como el producto de números primos. Estos números primos son la clave que revelan los datos, pero son desconocidos para el público, solo pueden ser decodificados en la web a la que van dirigidos.

Descomponer un número en factores es una tarea fácil si los números son pequeños (ver los ejercicios resueltos), pero en este caso se usan como clave números primos de 100 dígitos, que al multiplicarlos dan números muchísimo mayores, cuya descomposición detallada supone una labor descomunal.

Ejercicios resueltos

– Ejercicio 1

Descomponer 1029 en factores primos.

Solución

1029 es divisible por 3. Se sabe porque al sumar sus dígitos la suma es múltiplo de 3: 1+0+2+9 = 12. Como el orden de los factores no altera el producto, podemos comenzar por allí:

1029    3

343

1029 = 3 × 343

Por otra parte 343 = 7³, entonces:

1029 = 3 × 7³ = 3 × 7 × 7× 7

Y ya que tanto 3 como 7 son números primos, esta es la descomposición de 1029.

– Ejercicio 2

Factorizar el trinomio x² + 42x + 432.

Solución

El trinomio se reescribe de la forma (x+a). (x+b) y necesitamos encontrar los valores de a y b, de tal forma que:

a+b = 42; a.b = 432

El número 432 se descompone en factores primos y de allí se elige, por tanteo, la combinación adecuada para que los factores sumados den 42.

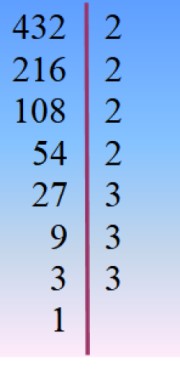
432 = 2⁴ × 3³ = 2× 3³× 2³ = 2⁴× 3² × 3 =…

A partir de aquí hay varias posibilidades para escribir 432:

432 = 16 ×27 = 24 × 18 = 54 × 8 = 6 × 72….

Y todas se pueden encontrar combinando productos entre los factores primos, pero para resolver el ejercicio propuesto, la única combinación adecuada es: 432 = 24 × 18 ya que 24 + 18 = 42, entonces:

x² + 42x + 432 = ( x + 24). (x +18)

Referencias

1. Baldor, A. 1986. Aritmética teórico práctica. Compañía Cultural Editora de Textos Americanos S.A.
2. BBC Mundo. El Código oculto de la Naturaleza. Recuperado de: bbc.com.
3. De Leon, Manuel.Números primos: los guardianes de internet. Recuperado de: blogs.20minutos.es.
4. UNAM. Teoría de Números I: Teorema fundamental de la Aritmética. Recuperado de: teoriadenumeros.wikidot.com.
5. Wikipedia. Teorema Fundamental de la Aritmética. Recuperado de: es.wikipedia.org.