Conjunto finito: propiedades, ejemplos, ejercicios resueltos
Se entiende por conjunto finito todo conjunto con un número limitado o contable de elementos. Ejemplos de conjuntos finitos son las canicas que están contenidas en una bolsa, el conjunto de las viviendas en un vecindario, o el conjunto P formado por los veinte (20) primeros números naturales:
P = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 15, 16, 17, 18, 19, 20}
El conjunto de las estrellas del universo con toda seguridad es inmenso, pero no se sabe a ciencia cierta si es finito o infinito. Sin embargo, el conjunto de los planetas del sistema solar es finito.
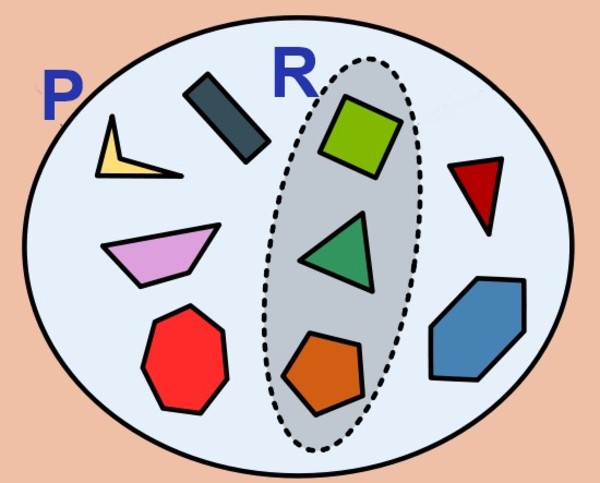
A el número de elementos de un conjunto finito se le llama su cardinalidad y para el conjunto P se denota así: Card(P) o #P. El conjunto vacío tiene cardinalidad cero y se considera un conjunto finito.
Índice del artículo
Entre las propiedades de los conjuntos finitos se tienen las siguientes:
1- La unión de conjuntos finitos da lugar a un nuevo conjunto finito.
2- Si dos conjunto finitos se interceptan, resulta un nuevo conjunto finito.
3- Un subconjunto de un conjunto finito es finito y su cardinalidad es menor o igual a la del conjunto original.
4- El conjunto vacío es un conjunto finito.
Son muchos los ejemplos de conjuntos finitos. Entre algunos ejemplos están los siguientes:
El conjunto M de los meses del año, que en forma extendida puede escribirse así:
M = {enero, febrero, marzo, abril, mayo, junio, julio, agosto, septiembre, octubre, noviembre, diciembre}, la cardinalidad de M es 12.
El conjunto S de los días de la semana: S = { lunes, martes, miércoles, jueves, viernes, sábado, domingo }. La cardinalidad de S es 7.
El conjunto Ñ de las letras del abecedario español es un conjunto finito, este conjunto por extensión se escribe así:
Ñ = { a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z } y su cardinalidad es 27.
El conjunto V de las vocales en español es un subconjunto del conjunto Ñ:
V ⊂ Ñ por lo tanto es un conjunto finito.
El conjunto finito V en forma extensiva se escribe así: V = { a, e, i, o, u } y su cardinalidad es 5.
Los conjuntos pueden ser expresados por comprensión. El conjunto F conformado por las letras de la palabra “finito” es un ejemplo:
F = { x / x es una letra de la palabra “finito” }
Dicho conjunto expresado en forma extensiva será:
F = { f, i, n, t, o } cuya cardinalidad es 5 y por tanto es un conjunto finito.
Los colores del arcoíris es otro ejemplo de conjunto finito, el conjunto C de estos colores es:
C = { rojo, naranja, amarillo, verde, cian, azul, violeta } y su cardinalidad es 7.
El conjunto de las fases F de la Luna es otro ejemplo de conjunto finito:
F = { luna Nueva, cuarto creciente, luna llena, cuarto menguante } este conjunto tiene cardinalidad 4.
Otro conjunto finito es el formado por los planetas del sistema solar:
P = { Mercurio, Venus, Tierra, Marte, Júpiter, Saturno, Urano, Neptuno, Plutón } de cardinalidad 9.
Se da el siguiente conjunto A = { x∊ R / x^3 = 27 }. Expresarlo en palabras y escribirlo por extensión, indicar su cardinalidad y decir si es o no es finito.
Solución: El conjunto A es el conjunto de los números reales x tal que x elevado al cubo de como resultado 27.
La ecuación x^3 = 27 tiene tres soluciones: que son x1 = 3, x2 = (-3/2 + 3√3/2 i) y x3= (-3/2 – 3√3/2 i). De las tres soluciones solo x1 es real, mientras que las otros dos son números complejos.
Como la definición del conjunto A dice que x pertenece a los números reales, entonces las soluciones en los números complejos no forman parte del conjunto A.
El conjunto A expresado extensivamente es:
A = { 3 }, el cual es un conjunto finito de cardinalidad 1.
Escribir en forma simbólica (por comprensión) y en forma extensiva el conjunto B de los números reales que son mayores que 0 (cero) y menores o iguales que 0 (cero). Indique su cardinalidad y si es o no es finito.
Solución: B = { x∊ R / 0 x = 0 }
El conjunto B es vacío porque un número real x no puede ser simultáneamente mayor y menor que cero, así como tampoco puede ser 0 y también menor que 0.
B = { } y su cardinalidad es 0. El conjunto vacío es un conjunto finito.
Se da el conjunto S de las soluciones de cierta ecuación. El conjunto S por comprensión se escribe así:
S = { x∊ R / (x-3)(x^2 – 9x + 20) = 0 }
Escribir dicho conjunto en forma extensiva, indicar su cardinalidad e indicar si es o no un conjunto finito.
Solución: En primer lugar, al analizar la expresión que describe al conjunto S, se obtiene que se trata de un conjunto de valores x reales que son soluciones de la ecuación:
(x-3)(x^2 – 9x + 20) = 0 (*)
Una solución de dicha ecuación es x=3, el cual es un número real y por tanto pertenece a S. Pero hay más soluciones las que pueden obtenerse buscando las soluciones de la ecuación cuadrática:
( x^2 – 9x + 20 ) = 0
La expresión anterior puede factorizarse de la siguiente manera:
( x – 4 ) ( x – 5 ) = 0
Lo que nos conduce a dos soluciones más de la ecuación original (*) que son x = 4 y x = 5. En definitiva la ecuación (*) tiene como soluciones 3, 4 y 5.
El conjunto S expresado en forma extensiva queda así:
S = { 3, 4, 5 }, el cual tiene cardinalidad 3 y por lo tanto es un conjunto finito.
Se tienen dos conjuntos A = { 1, 5, 7, 9 ,11 } y B = { x ∊ N / x es par ^ x 10 }.
Escribir en forma explícita el conjunto B y encontrar la unión con el conjunto A. Hallar también la intercepción de estos dos conjuntos y concluir.
Solución: el conjunto B está conformado por los números naturales tales que sean pares y además sean menores que el valor 10, por lo tanto en conjunto B en forma extensiva se escribe así:
B = { 2, 4, 6, 8 }
La unión del conjunto A con el conjunto B es:
A U B = { 1, 2, 4, 5, 6, 7, 8, 9, 11 }
y la intercepción del conjunto A con el conjunto B se escribe así:
A ⋂ B = { } = Ø es el conjunto vacío.
Debe notarse que la unión y la intercepción de estos dos conjuntos finitos conducen a nuevos conjuntos, los cuales a su vez son también finitos.
- Fuentes, A. (2016). MATEMÁTICAS BÁSICAS. Una Introducción al Cálculo. Lulu.com.
- Garo, M. (2014). Mathematics: quadratic equations: How solve a quadratic equation. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matemáticas para administración y economía. Pearson Educación.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matemáticas 1 SEP. Umbral.
- Preciado, C. T. (2005). Curso de Matemáticas 3o. Editorial Progreso.
- Matemáticas 10 (2018). “Ejemplos de Conjuntos Finitos”. Recuperado de: matematicas10.net
- Rock, N. M. (2006). Algebra I Is Easy! So Easy. Team Rock Press.
- Sullivan, J. (2006). Álgebra y Trigonometría. Pearson Educación.
- Wikipedia. Conjunto Finito. Recuperado de: es.wikipedia.com
