Reactancia inductiva: qué es, fórmula, cálculo, ejemplos, ejercicios
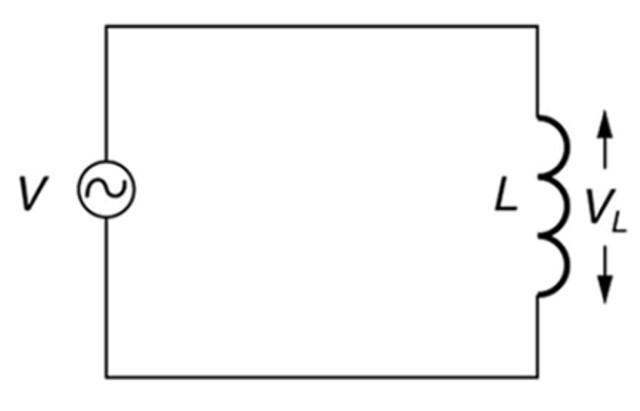
¿Qué es la reactancia inductiva?
La reactancia inductiva se refiere a la oposición que presenta la bobina al paso de la corriente, en un circuito alterno. En otras palabras, es la capacidad del inductor de reducir la corriente en un circuito alterno. Denotada como XL, su valor depende de la inductancia y de la frecuencia angular del voltaje:
XL= ω∙L
Donde ω es la frecuencia angular en radianes/s y L la inductancia, medida en henrios (H) en el Sistema Internacional de unidades SI.
Las inductancias grandes producen una gran reactancia inductiva, pues su resistencia al cambio es mayor. Y la reactancia aumenta asimismo con la frecuencia, así que una determinada inductancia L producirá una mayor reactancia, cuanto mayor sea la frecuencia del voltaje.
La unidad para la reactancia inductiva es el ohmio, simbolizado mediante Ω. Es la misma unidad de la resistencia eléctrica, pero a diferencia de esta, XL no es constante, ya que depende de la frecuencia del voltaje alterno aplicado.
Por lo tanto, en un circuito cuyos únicos elementos sean una fuente alterna y una inductancia (circuito inductivo), como el que se muestra en la figura de arriba, la reactancia inductiva va a depender de la frecuencia de la fuente.
No obstante, la analogía de XL con la resistencia eléctrica se puede extender al circuito inductivo, permitiendo la aplicación de la ley de Ohm. Si se define XL como el cociente entre las amplitudes del voltaje VL en el inductor, y la corriente IL que la atraviesa:
XL = VL / IL
Se puede escribir la ley de Ohm para circuitos puramente inductivos de la siguiente manera:
VL = XL∙IL
Fórmulas de la reactancia inductiva
Para calcular la reactancia inductiva se emplea la fórmula dada al comienzo, en la que L representa la inductancia (henrios) y ω es la frecuencia angular (radianes/segundo):
XL= ω∙L
Es común que la frecuencia se exprese en hertz o hertzio (Hz). En este caso se denota mediante f y se relaciona con la frecuencia angular a través de la fórmula:
ω = 2π∙f
En este caso, la reactancia se calcula como:
XL= 2πf∙L
En cualquiera de estas fórmulas, la reactancia inductiva resulta en ohmios, tal como se explicó previamente.
El efecto de la inductancia en un circuito inductivo
Debido a que la inductancia se opone a los cambios o variaciones de la corriente, la reactancia inductiva se caracteriza por retrasar la onda de corriente con respecto a la onda del voltaje.
En el siguiente gráfico, que muestra el voltaje VL (azul) y la corriente IL (rojo) en el inductor, ambos de forma senoidal, se observa que ambas ondas están desfasadas 90º. Comenzando en t = 0, el valor del voltaje es máximo, sin embargo, la corriente es nula en ese instante.
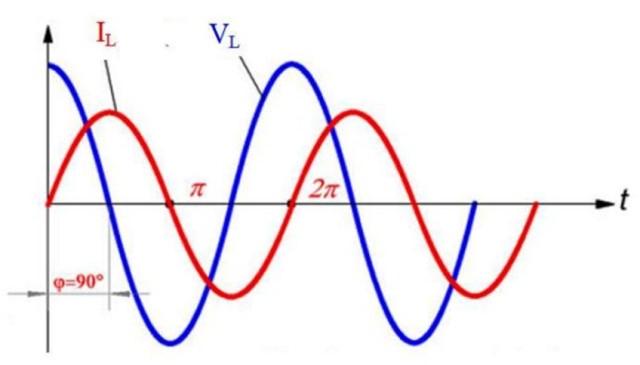
Más tarde, se observa que la corriente alcanza su valor máximo en t = π /2, pero para entonces el voltaje se anula e invierte su polaridad, es decir, se torna negativo. Simultáneamente, la corriente disminuye su valor, mientras el voltaje se vuelve más y más negativo.
Posteriormente, en t = π, el voltaje alcanza de nuevo su magnitud máxima, aunque con la polaridad invertida, y entonces la corriente se anula. De todo esto se desprende que siempre que VL llega a un pico, la corriente se anula, y cada vez que la corriente alcanza su magnitud máxima, el voltaje es 0.
La corriente siempre alcanza su pico después de que lo hace el voltaje, y ello se debe a que, como se dijo al comienzo, la inductancia se opone a los aumentos o disminuciones.
Cómo calcular la reactancia inductiva
Calcular la reactancia inductiva es muy sencillo: se precisa conocer el valor de la inductancia y la frecuencia del voltaje alterno aplicado. Luego, estos datos se sustituyen en alguna de las fórmulas dadas en la sección precedente y se efectúa la operación correspondiente.
Los siguientes ejemplos y ejercicios resueltos muestran la forma de hacerlo en diversas situaciones.
Ejemplos
Ejemplo 1
Supóngase un inductor de L = 5 mH, al cual se aplica un voltaje alterno de frecuencia 60.0 Hz. La reactancia inductiva en este caso se calcula mediante:
XL= 2πf∙L
Pero antes de sustituir los valores, la inductancia debe convertirse a henrios, multiplicando por el factor 1× 10−3. Por lo tanto:
L = 5 × 10−3 H
Entonces:
XL= 2πf∙L = XL= 2π × 60 Hz × 5 × 10−3 H = 1. 88 ohm
Ejemplo 2
Ahora se conecta la misma inductancia a un voltaje alterno de frecuencia distinta: 10.0 kHz. En este caso, la inductancia presenta una reactancia mayor:
XL= 2πf∙L = XL= 2π × 10.0 × 103 Hz × 5 × 10−3 H = 314.2 ohm
Ejemplo 3
El voltaje aplicado a la inductancia de los ejemplos 1 y 2 tiene un valor de 120 V rms. La respectiva corriente rms se determina a través de la ley de Ohm VL = XL∙IL:
IL = VL / XL
Para la frecuencia de 60.0 Hz, la corriente es:
IL = 120 V / 1. 88 ohm = 63.8 A
Y para la frecuencia de 10.0 kHz:
IL = 120 V / 314.2 ohm = 0.38 A
Puesto que en este último caso la reactancia es mucho mayor, es de esperar que la corriente sea más pequeña. Esta propiedad convierte al inductor en un filtro de altas frecuencias, una característica que se aprovecha para reducir los sonidos de alta frecuencia en los equipos de sonido, o para proteger los dispositivos de las subidas bruscas de corriente, entre otras aplicaciones.
Ejercicios resueltos
Ejercicio 1
Determinar la reactancia inductiva en un circuito que consiste en una inductancia de 2.5 mH, en serie con una fuente de voltaje alterno, cuya frecuencia es de 75 r.p.m.
Solución
Una revolución o ciclo completo equivale a 2π radianes, y un minuto tiene 60 segundos, por lo tanto, una frecuencia de 75 r.p.m equivale a:
75 r.p.m = 75 × 2π radianes / 60 segundos = 7.85 radianes/s
Y con este valor, la reactancia es:
XL= ω∙L = (7.85 radianes/s) × 2.5 × 10−3 H = 0.02 Ω
Ejercicio 2
Se utiliza una inductancia en serie con la fuente de una computadora para filtrar el ruido proveniente de las altas frecuencias.
a) ¿Cuál debe ser el valor mínimo de la inductancia necesaria para producir una reactancia de 2 kΩ, si la frecuencia de la señal que se quiere filtrar es de 15 kHz?
b) Hallar la reactancia de este inductor a la frecuencia de 60 Hz.
Solución a
XL = 2 kΩ = 2000 Ω
f = 15 kHz = 15000 Hz
Por lo tanto, despejando de la ecuación XL= 2πf∙L, se tiene:
L = XL / 2π∙f = 2000 Ω / 2π×15000 Hz = 0.0212 H = 21.2 mH
Solución b
Usando nuevamente XL= 2πf∙L, pero con f = 60 Hz, resulta:
XL= 2π×60 Hz×0.0212 H = 8 ohm.
Referencias
- Bauer, W. (2011). Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Giancoli, D. (2006). Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Katz, D. (2013). Physics for Scientists and Engineers. Foundations and Connections. Cengage Learning.
- Open Stax. College Physics. Recuperado de: openstax.org.
- Sears, Z. (2016). University Physics with Modern Physics. 14th. Ed. Volume 2. Pearson
