Función inyectiva: en qué consiste, para qué sirve y ejemplos

Una función inyectiva es toda relación de elementos del dominio con un único elemento del codominio. También conocidas como función uno a uno ( 1 – 1 ), son parte de la clasificación de funciones con respecto a la forma en que se relacionan sus elementos.

Un elemento del codominio solo podrá ser imagen de un único elemento del dominio, de esta forma los valores de la variable dependiente no pueden repetirse.

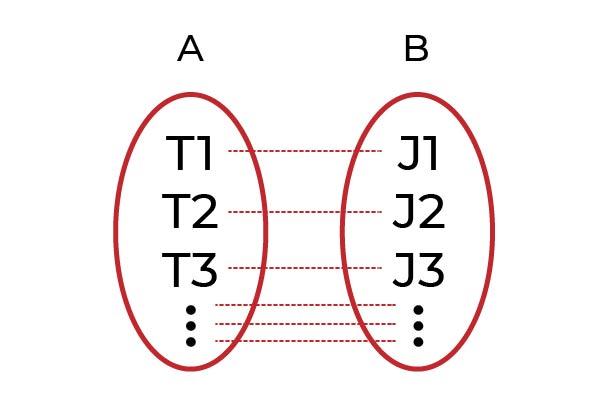
Un claro ejemplo sería agrupar a los hombres con trabajo en un grupo A, y en un grupo B a todos los jefes. La función F será la que asocie a cada trabajador con su jefe. Si cada trabajador está asociado con un jefe diferente a través de F, entonces F  será una función inyectiva.

Para considerar inyectiva a una función se debe cumplir lo siguiente:

∀ x₁  ≠ x₂   ⇒ F( x₁ ) ≠ F( x₂ )

Esta es la forma algebraica de decir Para todo x₁ diferente de x₂ se tiene un F( x₁ ) diferente de   F( x₂ ).

Índice del artículo

• 1 ¿Para qué sirven las funciones inyectivas?
  • 1.1 Condicionamiento de funciones
• 2 Ejemplos de funciones inyectivas con ejercicios resueltos
  • 2.1 Ejemplo 1
  • 2.2 Ejemplo 2
  • 2.3 Ejemplo 3
  • 2.4 Ejemplo 4
  • 2.5  Ejemplo 5
  • 2.6 Ejemplo 6
  • 2.7 Ejemplo 7
• 3 Ejercicios propuestos para clase/casa
• 4 Referencias

¿Para qué sirven las funciones inyectivas?

La inyectividad es una propiedad de las funciones continuas, ya que aseguran la asignación de imágenes para cada elemento del dominio, aspecto esencial en la continuidad de una función.

Al trazar una línea paralela al eje X sobre la gráfica de una función inyectiva, solo se debe tocar a la gráfica en un solo punto, sin importar a que altura o magnitud de Y se trace la recta. Esta es la manera gráfica de probar la inyectividad de una función.

Otra manera de probar si una función es inyectiva, es despejando la variable independiente X en términos de la variable dependiente Y. Luego se debe verificar si el dominio de esta nueva expresión contiene a los números reales, al mismo tiempo que para cada valor de Y exista un único valor de X.

Las funciones o relaciones de orden obedecen, entre otras formas, a la notación F : D_f→C_f

Que se lee F que va desde D_f hasta C_f

Donde la función F relaciona los conjuntos Dominio y Codominio. También conocidos como conjunto de partida y conjunto de llegada.

El dominio D_f  contiene los valores permitidos para la variable independiente. El codominio C_f  está formado por todos los valores disponibles a la variable dependiente. Los elementos de C_f relacionados a D_f  se conocen como Rango de la función ( R_f ).

Condicionamiento de funciones

En ocasiones una función que no es inyectiva, puede someterse a ciertos condicionamientos. Estás nuevas condiciones pueden convertirla en una función inyectiva. Son válidas todo tipo de modificaciones al dominio y codominio de la función, donde el objetico es cumplir las propiedades de inyectividad en la relación correspondiente.

Ejemplos de funciones inyectivas con ejercicios resueltos

Ejemplo 1

Sea la función F : R → R definida por la recta F ( x ) = 2x – 3

R : [ Todos los números reales ]

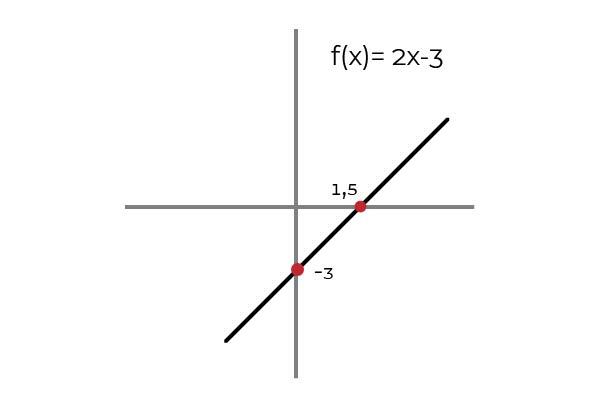
Se observa que para todo valor del dominio existe una imagen en el codominio. Esta imagen es única lo cual hace de F sea una función inyectiva. Esto aplica para todas las funciones lineales (Funciones cuyo mayor grado de la variable es uno).

Ejemplo 2

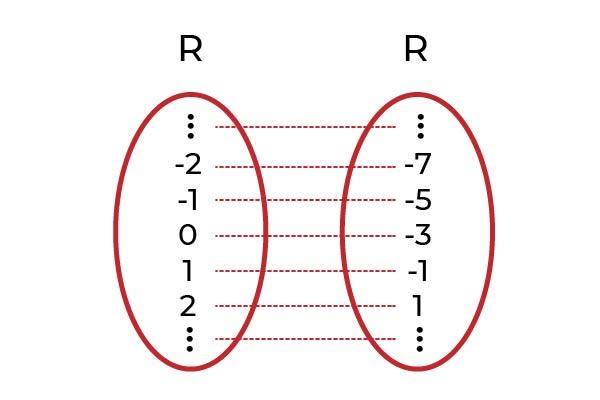
Sea la función F : R → R definida por F ( x ) = x² +1

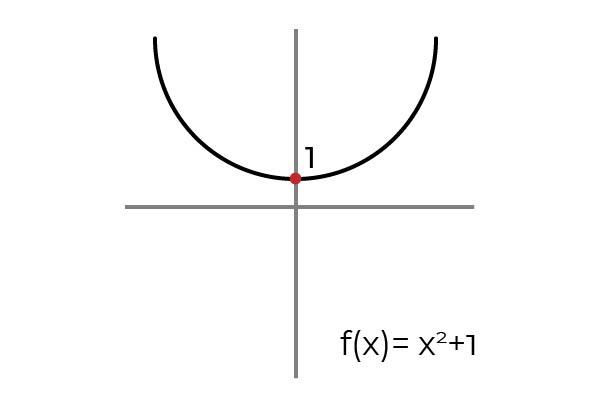
Al trazar una línea horizontal, se observa que la gráfica es encontrada en más de una ocasión. Debido a esto la función F no es inyectiva mientras esté definida  R → R

Se procede a condicionar el dominio de la función:

                                               F : R⁺U { 0 } → R

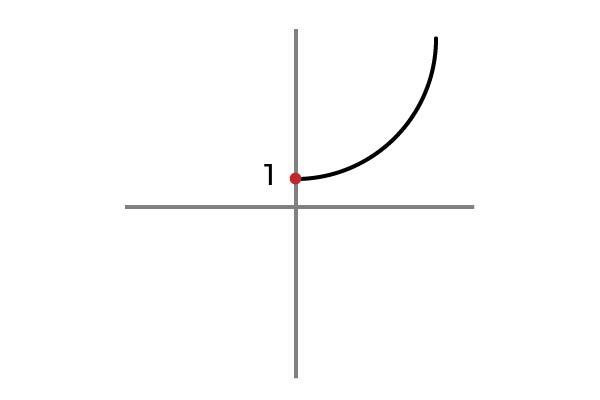
Ahora la variable independiente no toma valores negativos, de esta forma se evita repetir resultados y la función F : R⁺U { 0 } → R definida por F ( x ) = x² + 1 es inyectiva.

Otra solución homóloga sería acotar el dominio por la izquierda, es decir restringir a la función para solo tomar valores negativos y cero.

Se procede a condicionar el dominio de la función

                                               F : R^–U { 0 } → R

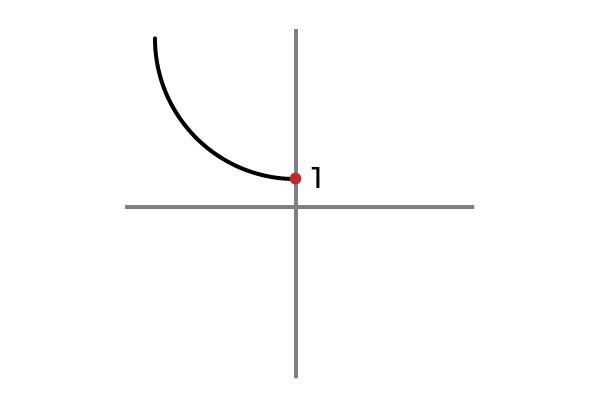
Ahora la variable independiente no toma valores negativos, de esta forma se evita repetir resultados y la función F : R^–U { 0 } → R definida por F ( x ) = x² + 1 es inyectiva.

Las funciones trigonométricas poseen comportamientos similares a ondas, en donde es muy común encontrar repeticiones de valores en la variable dependiente. A través de condicionamientos específicos, basados en el conocimiento previo de dichas funciones, podemos acotar el dominio para cumplir las condiciones de inyectividad.

Ejemplo 3

Sea la función F : [ –π/2 , π/2 ] → R definida por F ( x ) = Cos ( x )

En el intervalo [ –π/2 → π/2 ] la función coseno varía sus resultados entre cero y uno.

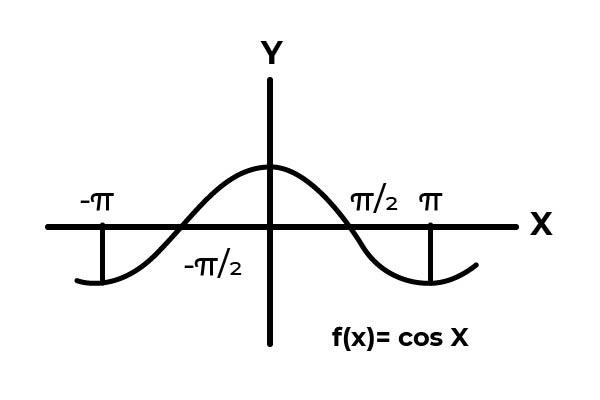
Tal como se aprecia en la gráfica. Comienza desde cero en x =–π/2 alcanzando luego un máximo en cero. Es después de x = 0 que los valores empiezan a repetirse, hasta volver a cero en x = π/2. De esta forma se sabe que F ( x ) = Cos ( x ) no es inyectiva para el intervalo [ –π/2 , π/2 ] .

Al estudiar la gráfica de la función F ( x ) = Cos ( x ) se observan intervalos donde el comportamiento de la curva se adapta a los criterios de inyectividad. Como por ejemplo el intervalo

[ 0 , π ]

Donde la función varía resultados desde 1 hasta -1, sin repetir ningún valor en la variable dependiente.

De esta forma la función función F : [ 0 , π ] → R definida por F ( x ) = Cos ( x ). Es inyectiva

Existen funciones no lineales donde se presentan casos similares. Para las expresiones de tipo racional, donde el denominador alberga al menos una variable, existen restricciones que impiden la inyectividad de la relación.

Ejemplo 4

Sea la función F : R → R definida por F ( x ) = 10/x

La función está definida para todos los números reales excepto { 0 } quien presenta una indeterminación (No se puede dividir entre cero).

Al acercarse a cero por la izquierda la variable dependiente toma valores negativos muy grandes, e inmediatamente luego de cero, los valores de la variable dependiente toman cifras positivas grandes.

Esta disrupción hace que la expresión F : R → R definida por F ( x ) = 10/x

No sea inyectiva.

Como se vio en los ejemplos anteriores, la exclusión de valores en el dominio sirve para “reparar” estas indeterminaciones. Se procede a excluir al cero del dominio, quedando los conjuntos de partida y llegada definidos de la siguiente manera:

R – { 0 } → R

Donde R – { 0 } simboliza a los reales exceptuando un conjunto cuyo único elemento es cero.

De esta manera la expresión F : R – { 0 } → R definida por F ( x ) = 10/x  es inyectiva.

 Ejemplo 5

Sea la función F : [ 0 , π ] → R definida por F ( x ) = Sen ( x )

En el intervalo [ 0 , π ] la función seno varía sus resultados entre cero y uno.

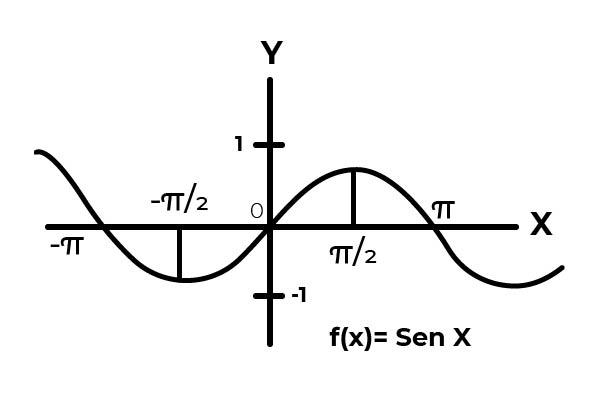
Tal como se aprecia en la gráfica. Comienza desde cero en x =0 alcanzando luego un máximo en x = π/2. Es después de x = π/2 que los valores empiezan a repetirse, hasta volver a cero en x = π. De esta forma se sabe que F ( x ) = Sen ( x ) no es inyectiva para el intervalo [ 0 , π ] .

Al estudiar la gráfica de la función F ( x ) = Sen ( x ) se observan intervalos donde el comportamiento de la curva se adapta a los criterios de inyectividad. Como por ejemplo el intervalo  [  π/2  ,3π/2  ]

Donde la función varía resultados desde 1 hasta -1, sin repetir ningún valor en la variable dependiente.

De esta forma la función F : [  π/2  ,3π/2  ] → R definida por F ( x ) = Sen ( x ). Es inyectiva

Ejemplo 6

Verificar si la función F : [ 0 , ∞ ) → R definida por F ( x ) = 3x² es inyectiva.

En esta ocasión el dominio de la expresión ya se encuentra acotado. Se observa además que los valores de la variable dependiente no se repiten en este intervalo.

Por lo cual se puede concluir que F : [ 0 , ∞ ) → R definida por F ( x ) = 3x²   es inyectiva

Ejemplo 7

Identifica cuál de las siguientes funciones es

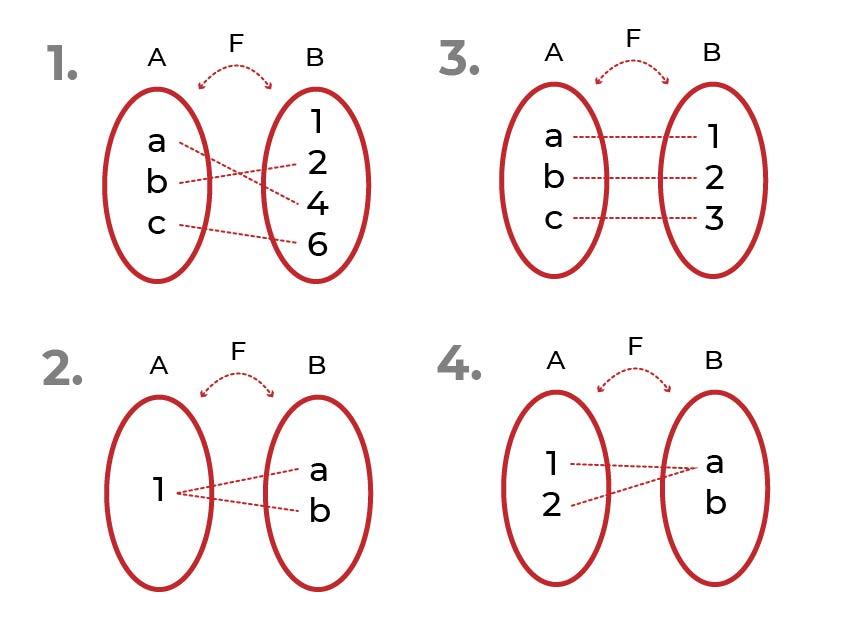
1. Es inyectiva. Los elementos asociados del codominio son únicos para cada valor de la variable independiente.
2. No es inyectiva. Existen elementos del codominio asociados a más de un elemento del conjunto de partida.
3. Es inyectiva
4. No es inyectiva

Ejercicios propuestos para clase/casa

Verificar si las siguientes funciones son inyectivas:

F : [ 0 , ∞ ) →R definida por F ( x ) = (x + 3)²  

F : [ π/2  ,3π/2  ] → R definida por F ( x ) = Tan ( x )

F : [ –π  ,π  ] → R definida por F ( x ) = Cos ( x + 1)

F : R →R definida por la recta F ( x ) = 7x + 2

Referencias

1. Introduction to Logic and Critical Thinking. Merrilee H. Salmon. University of Pittsburgh
2. Problems in Mathematical Analysis. Piotr Biler, Alfred Witkowski. University of Wroclaw. Poland.
3. Elements of Abstract Analysis. Mícheál O’Searcoid PhD. Department of mathematics. University college Dublin, Beldfield, Dublind 4.
4. Introduction to Logic and to the Methodology of the Deductive Sciences. Alfred Tarski, New York Oxford. Oxford University press.
5. Principios de análisis matemático. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona España.