Gravicentro: qué es, definición, ejemplos, ejercicios resueltos
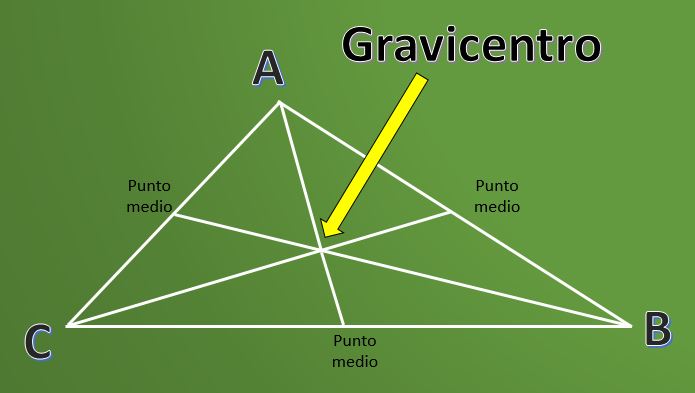
¿Qué es el gravicentro?
El gravicentro es una definición que es muy utilizada en geometría cuando se está trabajando con triángulos. Para comprender la definición de gravicentro es necesario primero conocer la definición de “medianas” de un triángulo.
Las medianas de un triángulo son los segmentos de recta que parten en cada vértice y llegan al punto medio del lado opuesto a dicho vértice.
El punto de intersección de las tres medianas de un triángulo es llamada baricentro o también es conocido como gravicentro. No basta con solo conocer la definición, es interesante saber cómo se calcula este punto.
Cálculo del baricentro
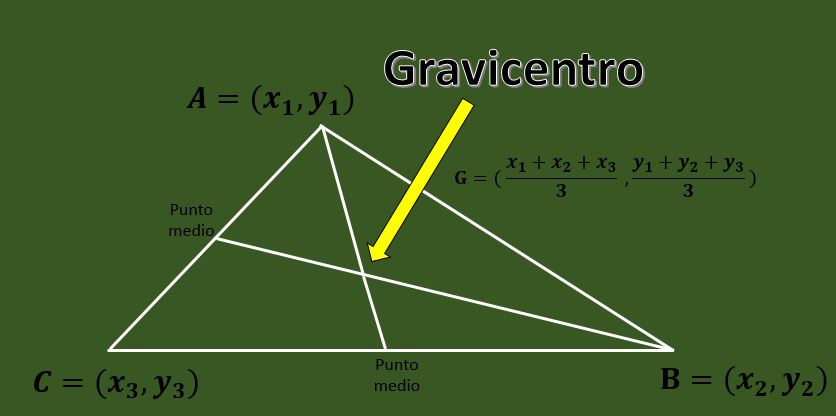
Dado un triángulo ABC con vértices A=(x1,y1), B=(x2,y2) y C=(x3,y3), se tiene que el gravicentro es la intersección de las tres medianas del triángulo.
Una fórmula rápida que permite el cálculo del gravicentro de un triángulo, siendo conocidas las coordenadas de sus vértices es:
G = ( (x1+x2+x3)/3 , (y1+y2+y3)/3 ).
Con esta fórmula se puede saber la ubicación del gravicentro en el plano cartesiano.
Características del gravicentro
No hace falta trazar las tres medianas del triángulo, pues al trazar dos de ellas quedará evidenciado dónde está el gravicentro.
El gravicentro divide a cada mediana en 2 partes cuya proporción es 2:1, es decir, los dos segmentos de cada mediana quedan divididos en segmentos de longitudes 2/3 y 1/3 de la longitud total, siendo la distancia mayor la que hay entre el vértice y el gravicentro.
La siguiente imagen ilustra mejor esta propiedad.
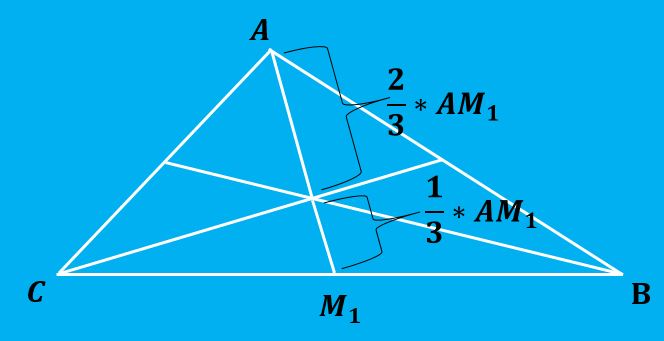
La fórmula para el cálculo del gravicentro es muy sencilla de aplicar. La forma de obtener esta fórmula es calculando las ecuaciones de recta que definen cada mediana y luego hallar el punto de corte de dichas rectas.
Ejercicios
A continuación se presenta una pequeña lista de problemas sobre el cálculo del baricentro.
1.- Dado un triángulo de vértices A=(0,0), B=(1,0) y C=(1,1), calcule el gravicentro de dicho triángulo.
Utilizando la fórmula dada, se puede concluir rápidamente que el gravicentro del triángulo ABC es:
G = ( (0+1+1)/3 , (0+0+1)/3 ) = ( 2/3 , 1/3 ).
2.- Si un triángulo tiene vértices A=(0,0), B=(1,0) y C=(1/2,1), ¿cuáles son las coordenadas del gravicentro?
Ya que son conocidos los vértices del triángulo se procede a aplicar la fórmula para el cálculo del gravicentro. Por lo tanto, el gravicentro tiene coordenadas:
G = ( (0+1+1/2)/3 , (0+0+1)/3 ) = ( 1/2 , 1/3 ).
3.- Calcule los posibles gravicentros para un triángulo equilátero tal que dos de sus vértices son A=(0,0) y B=(2,0).
En este ejercicio solo se están especificando dos vértices del triángulo. Para poder halla los posibles gravicentros se debe primero calcular el tercer vértice del triángulo.
Ya que el triángulo es equilátero y la distancia entre A y B es 2, se tiene que el tercer vértice C, debe estar a distancia 2 de A y de B.
Utilizando el hecho que en un triángulo equilátero la altura coincide con la mediana y además utilizando el teorema de Pitágoras, se puede concluir que las opciones para las coordenadas del tercer vértice son C1=(1, √3) o C2=(1, -√3).
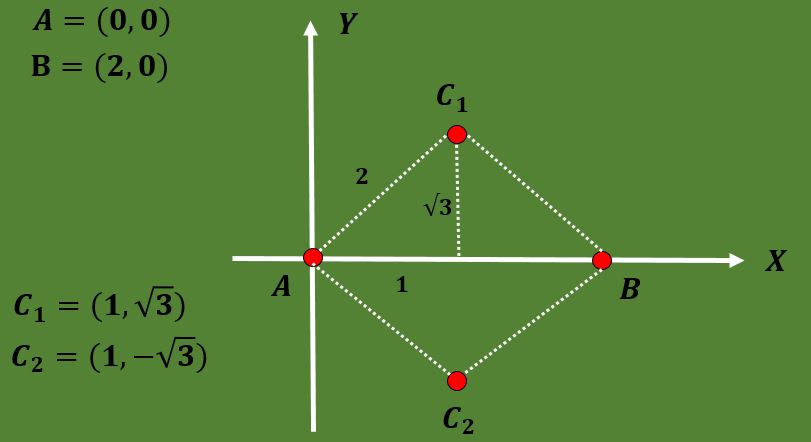
De modo que las coordenadas de los dos posibles gravicentros son:
G1= ( (0+2+1)/3, (0+0+√3)/3) = (3/3 , √3/3) = (1, √3/3),
G2= ( (0+2+1)/3, (0+0-√3)/3) = (3/3 , -√3/3) = (1, -√3/3).
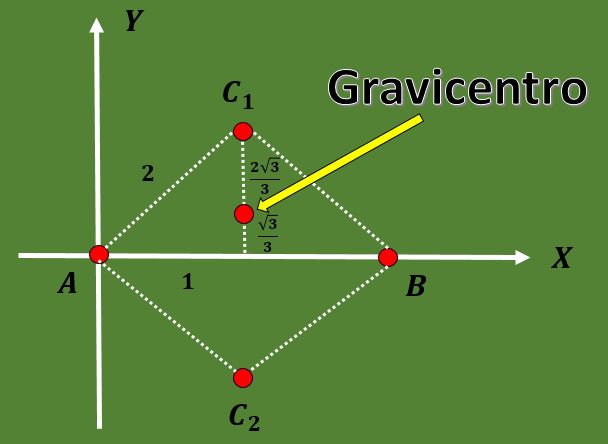
Gracias a las cuentas anteriores también se puede notar que la mediana quedo dividida en dos partes cuya proporción es 2:1.
