Leyes de De Morgan: explicación, demostración y ejemplos

¿Qué son las leyes de De Morgan?
Las leyes de De Morgan son dos leyes lógicas pertenecientes a la lógica proposicional que fueron formuladas por el matemático inglés Augustus De Morgan (1806-1871). En ellas se establece lo siguiente, respecto a una proposición lógica compuesta:
- El opuesto de una conjunción es equivalente a la disyunción que se forma con los opuestos o negaciones de las proposiciones que conforman la conjunción.
- La negación de la disyunción se puede expresar como una conjunción conformada por los opuestos o negaciones de las proposiciones involucradas en la disyunción.
En la notación de la lógica proposicional, las leyes de De Morgan se expresan de una forma compacta y más formal así:
- ∼(p ∧ q) ⇔ ∼p ∨ ∼q
- ∼(p ∨ q) ⇔ ∼p ∧ ∼q
Lo que expresan estas leyes es que, ya sea en la negación de la conjunción o de la disyunción, el resultado es equivalente a negar por separado a cada una de las proposiciones participantes e invertir el conector que las vincula.
Para una mejor comprensión de las leyes de De Morgan, es necesario revisar el significado de las proposiciones y de los símbolos empleados en lógica proposicional, para ver como aplicar convenientemente estas leyes.
Notación lógica
La herramienta básica de la lógica proposicional son las proposiciones. Una proposición lógica es un enunciado que admite un valor de verdad, ya sea que este sea cierto o falso, pero no ambas cosas a la vez. En esto no se permite ambigüedad alguna, es decir, no puede haber dudas.
Una proposición se denota con una minúscula, como en los siguientes ejemplos:
- p: Ciudad de México es la capital de México (cierta).
- q: Al sumar 2 y 3 se obtiene 4 (falsa).
- r: Todos los mamíferos son animales terrestres (falsa).
También hay proposiciones más complejas, que se estructuran mediante el uso de proposiciones simples, como estas:
- p: Carlos irá al cine si no llueve.
- q: Ana es químico o biólogo marino.
- r: Juan va a cenar o Pedro verá el partido por televisión.
Conectores lógicos
Los conectores lógicos son símbolos usados para enlazar proposiciones simples y así construir proposiciones más complejas. En la lógica proposicional cada uno de ellos tiene un significado particular.
Los conectores más usados son conjunción, disyunción, disyunción exclusiva, negación, condicionalidad y bi-condicionalidad.
Conjunción
La conjunción se denota con una letra “v” invertida. Una proposición compuesta a través de una conjunción se simboliza p ∧ q, como sigue:
- p ∧ q: Ciudad de México es la capital de México y está en Norteamérica.
Es fácil identificar aquí que p es “Ciudad de México es la capital de México” y q es “Está en Norteamérica”.
Disyunción
Se distinguen dos tipos de disyunción: la débil y la exclusiva. Una disyunción débil se simboliza mediante ∨ y en notación lógica sería p ∨ q. Ejemplo de esta clase de disyunción es:
- p ∨ q: Juan es futbolista o Juan es tenista.
En cambio, la disyunción exclusiva se simboliza mediante el signo ⊻ e implica que una de las proposiciones debe descartarse, por ejemplo:
p ⊻ q: Alicia tiene 20 años o Alicia tiene 22 años.
La diferencia entre ambos tipos es clara, en la disyunción exclusiva, una de las proposiciones se descarta, ya que si Alicia tiene 20 años, no puede tener 22 y viceversa. En cambio en la disyunción débil puede que Juan sea futbolista y tenista a la vez.
Negación
Al anteponer el símbolo ∼ a una proposición, se niega esta, como en:
- p: ∼(Veracruz es la capital de México).
Que se lee como “Veracruz no es la capital de México”. Otras formas de expresar una negación, aparte del “no”, es mediante frases como “es falso”, “es mentira que” y “no es cierto que”.
Condicionalidad
Son proposiciones compuestas que suelen emplear las palabras “si” y “entonces…” para vincular dos proposiciones en las que existe condicionalidad o implicación. La parte de la proposición que se escribe inmediatamente después del “si” es el antecedente o la hipótesis de la proposición y lo que está luego del término “entonces” es la conclusión o consecuente.
El símbolo que se usa para la condicionalidad es la flecha de izquierda a derecha “→”, por lo tanto una condicionalidad entre dos proposiciones se representa como p → q, que puede leerse como “Si p, entonces q”. Por ejemplo:
p → q: Si llueve durante la tarde entonces no jugaré tenis.
Bi-condicionalidad
En este tipo de proposición se emplea la frase “si, y solo si” para conectar dos proposiciones, llamadas primero y segundo miembro de la bicondicional. El símbolo empleado es la flecha bidireccional “↔”.
Las dos proposiciones conectadas por medio de “si, y solo si” se llaman respectivamente primero y segundo miembro y la bi-condicionalidad de dos proposiciones p y q queda como p ↔ q. Por ejemplo:
p ↔ q : A María le gusta montar en bicicleta si y solo si el día está soleado.
Demostración de las leyes de De Morgan
Las leyes de De Morgan forman parte de las equivalencias lógicas y se pueden demostrar a través de las tablas de verdad, que se usan para conocer el valor de verdad (cierto o falso) de una proposición.
Puesto que la conjunción solo es verdadera cuando p y q son verdaderas, su tabla de verdad es:
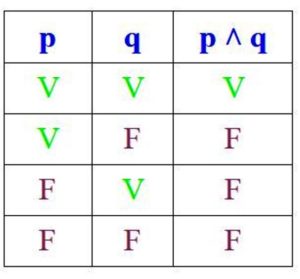
Por otra parte, en la disyunción, la proposición es verdadera si p y q son verdaderas o si al menos una de ellas lo es, pero es falsa si ambas lo son:
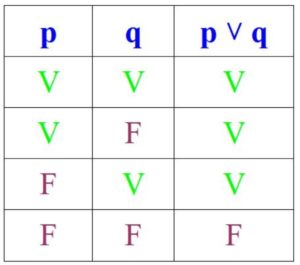
Ahora bien, la negación transforma lo cierto en falso y viceversa. En tal caso, los valores de verdad de ∼(p ∧ q) y ∼(p ∨ q) son lo contrario de los valores de verdad de (p ∧ q) y (p ∨ q):

Y hay que comprobar que se obtienen estos resultados al llevar a cabo las tablas de verdad respectivas de (∼ p ˅ ∼ q) y (∼ p ˄ ∼ q):
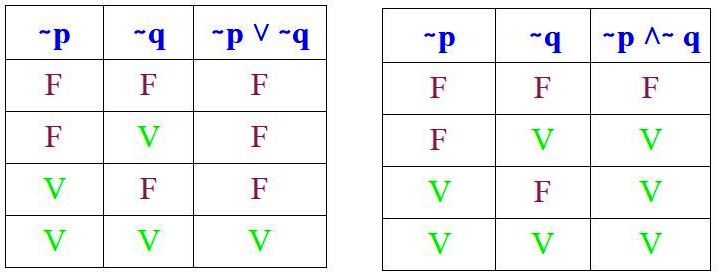
Y en efecto, al comparar las respectivas tablas de verdad, se observa que las leyes de De Morgan se cumplen. Ahora se verán dos ejemplos de su aplicación.
Ejemplo resuelto 1
Aplicar las leyes de De Morgan para hallar la expresión equivalente de: ∼ (∼p ˅ ∼q)
- Solución
Se compara la expresión dada ∼ (∼p ˅ ∼q) con la ley de Morgan:
∼(p ∨ q) ⇔ ∼p ∧ ∼q
Y se observa que la negación ya se encuentra fuera del paréntesis en ambos casos, por lo tanto se siguen las instrucciones de la ley: se niega a ∼p, se niega a ∼q y se cambia el conector:
∼ (∼p ˅ ∼q) ⇔ ∼ (∼p) ∧ ∼ (∼q) ⇔ p ∧ q
Ejemplo resuelto 2
Determinar la expresión equivalente de ∼ [∼p ˄ ∼ (∼q)] ≡
- Solución
En primer lugar se simplifica la negación de ∼q:
∼ [∼p ˄ ∼ (∼q)] ⇔ ∼ [∼p ˄ q]
Como ya hay una negación fuera del corchete, la expresión resultante se compara con la ley de Morgan: ∼(p ∧ q) ⇔ ∼p ∨ ∼q
Para resolver ∼ [∼p ˄ q] hay que negar a ∼p, negar a q y cambiar el conector:
∼ [∼p ˄ q] ⇔∼(∼p) ∨ ∼q ⇔ p ˅ ∼q
Referencias
- Becerra, J.M. Apuntes de lógica de la UNAM.
- Brilliant. De Morgan’s Laws. Recuperado de: brilliant.org.
- Electronics Tutorials. De Morgan’s Theorem. Recuperado de: electronics-tutorials.ws.
- López, F. Introducción a la lógica matemática. Recuperado de: youtube.com
- Muñoz, C. Introducción a la lógica. Recuperado de: webs.ucm.es.
