Coeficiente de restitución: concepto, fórmula, cálculo, ejemplo
El coeficiente de restitución es el cociente entre la velocidad relativa de alejamiento y la velocidad relativa de acercamiento de dos cuerpos que colisionan. Cuando los cuerpos quedan unidos después de la colisión, dicho cociente es nulo. Y vale la unidad en el caso que la colisión sea perfectamente elástica.
Supongamos dos esferas sólidas de masa M1 y masa M2 respectivamente que sufren una colisión. Justo antes de la colisión las esferas tenían velocidades V1 y V2 respecto a cierto sistema inercial de referencia. Justo después de la colisión sus velocidades cambian a V1’ y V2’.
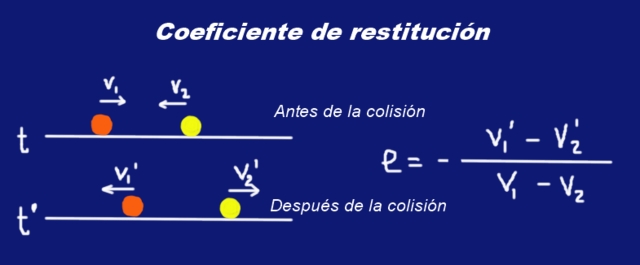
Se ha colocado letra negrita en las velocidades para indicar que las mismas se tratan de cantidades vectoriales.
Los experimentos indican que toda colisión cumple la siguiente relación:
V1’ – V2’ = -e ( V1 – V2 )
Donde e es un número real comprendido entre 0 y 1, llamado el coeficiente de restitución de la colisión. La expresión anterior se interpreta así:
La velocidad relativa de dos partículas antes de la colisión es proporcional a la velocidad relativa de las dos partículas después de la colisión, la constante de proporcionalidad es (-e), donde e es el coeficiente de restitución de la colisión.
Índice del artículo
- 1 ¿Para qué sirve el coeficiente de restitución?
- 2 ¿Cómo se calcula el coeficiente de restitución?
- 3 Ejemplo
- 4 Referencias
La utilidad de este coeficiente radica en conocer el grado de inelasticidad de una colisión. En caso que la colisión sea perfectamente elástica el coeficiente será 1, mientras que en una colisión completamente inelástica el coeficiente valdrá 0, ya que en este caso, la velocidad relativa después de la colisión es nula.
Recíprocamente, si se conoce el coeficiente de restitución de una colisión y las velocidades de las partículas antes de ella, entonces pueden predecirse las velocidades luego que ocurra dicha colisión.
En las colisiones, además de la relación que establece el coeficiente de restitución, hay otra relación fundamental, que es la conservación del momentum.
El momentum p de una partícula, o cantidad de movimiento como también se le denomina, es el producto de la masa M de la partícula por su velocidad V. Es decir: el momentum p es una cantidad vectorial.
En las colisiones el momentum lineal P del sistema es igual justo antes y justo después de la colisión, debido a que las fuerza exteriores son despreciables frente a las breves pero intensas fuerzas de interacción interna durante la colisión. Pero no basta con la conservación del momentum P del sistema para resolver el problema general de la colisión.
En el caso mencionado previamente, el de las dos esferas de masas M1 y M2 que colisionan, la conservación del momentum lineal se escribe así:
M1 V1 + M2 V2 = M1 V1’ + M2 V2’ .
No hay forma de resolver el problema de la colisión si no se conoce el coeficiente de restitución. La conservación del momentum, aunque necesaria, es insuficiente para predecir las velocidades después de la colisión.
Cuando un problema afirma que los cuerpos quedan moviéndose juntos después de la colisión, implícitamente dice que el coeficiente de restitución es 0.

La otra cantidad física importante que interviene en las colisiones es la energía. Durante las colisiones hay intercambios de energía cinética, energía potencial y otros tipos de energía, como la energía calórica.
Antes y después de la colisión la energía potencial de interacción es prácticamente nula, por eso el balance energético involucra la energía cinética de las partículas antes y después y una cantidad Q llamada energía disipada.
Para las dos esferas de masas M1 y M2 que colisionan el balance energético antes y después de la colisión se escribe así:
½ M1 V1^2 + ½ M2 V2^2 = ½ M1 V1’^2 + ½ M2 V2’^2 + Q
Cuando la fuerzas de interacción durante la colisión son puramente conservativas ocurre que la energía cinética total de las partículas que colisionan se conserva, es decir, es igual antes y después de la colisión (Q = 0). Cuando esto ocurre se dice que la colisión es perfectamente elástica.
En los casos de colisiones elásticas, no se disipa energía. Y además el coeficiente de restitución cumple: e = 1.
Por el contrario, en las colisiones inelásticas Q ≠ 0 y 0 ≤ e 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
Para que un problema de colisiones quede perfectamente determinado, es necesario conocer el coeficiente de restitución, o alternativamente la cantidad de energía disipada durante la colisión.
El coeficiente de restitución depende de la naturaleza y tipo de interacción entre los dos cuerpos durante la colisión.
Por su parte, la velocidad relativa de los cuerpos antes de la colisión definirá la intensidad de la interacción y de allí su influencia sobre el coeficiente de restitución.
Para ilustrar cómo se calcula el coeficiente de restitución de una colisión tomaremos un caso sencillo:
Supongamos la colisión de dos esferas de masas M1 = 1 kg y M2 = 2 kg que se mueven sobre un riel recto sin fricción (como en la figura 1).
La primera esfera incide con velocidad inicial V1 = 1 m/s sobre la segunda que originalmente está en reposo, es decir V2 = 0 m/s.
Después de la colisión quedan moviéndose así: la primera se detiene (V1’ = 0 m/s) y la segunda se mueve hacia la derecha con velocidad V2’ = 1/2 m/s.
Para calcular el coeficiente de restitución en esta colisión aplicamos la relación:
V1’ – V2’ = -e ( V1 – V2 )
0 m/s – 1/2 m/s = – e ( 1 m/s – 0 m/s) => – 1/2 = – e => e = 1/2 .
En la colisión unidimensional de las dos esferas de la sección anterior se calculó su coeficiente de restitución resultando ser e = ½ .
Como e≠1 la colisión no es elástica, es decir que la energía cinética del sistema no se conserva y hay cierta cantidad de energía disipada Q (por ejemplo calentamiento de las esferas a causa de la colisión).
Determine el valor de la energía disipada en Joules. También calcule la fracción porcentual de energía disipada.
La energía cinética inicial de la esfera 1 es:
K1i = ½ M1 V1^2 = ½ 1 kg (1 m/s)^2 = ½ J
mientras que la de la esfera 2 es cero por estar inicialmente en reposo.
Entonces la energía cinética inicial del sistema es Ki = ½ J.
Después de la colisión solo la segunda esfera se mueve con velocidad V2’ = ½ m/s, por lo que la energía cinética final del sistema será:
Kf = ½ M2 V2’^2 = ½ 2 kg (½ m/s)^2 = ¼ J
Es decir, la energía disipada en la colisión es:
Q = Ki – Kf = (½ J – ¼ J) = 1/4 J
Y la fracción de energía disipada en esta colisión se calcula de la siguiente manera:
f = Q / Ki = ¼ / ½ = 0,5 es decir que se ha disipado el 50% de la energía del sistema a causa de la colisión inelástica cuyo coeficiente de restitución es 0,5.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
- Wikipedia. Cantidad de movimiento.Recuperado de: es.wikipedia.org.
