Binomio conjugado: cómo se resuelve, ejemplos, ejercicios
Un binomio conjugado de otro binomio es aquel en el que solo se diferencian por un signo de la operación. El binomio, tal como su nombre lo indica, es una estructura algebraica que consta de dos términos.
Algunos ejemplos de binomios son: (a + b), (3m – n) y (5x – y). Y sus respectivos binomios conjugados son:(a – b), (-3m – n) y (5x + y). Como se aprecia de inmediato, la diferencia está en el signo.

Un binomio multiplicado por su conjugado da como resultado un producto notable que se utiliza muchísimo en álgebra y ciencia. El resultado de la multiplicación es la resta de los cuadrados de los términos del binomio original.
Por ejemplo, (x – y) es un binomio y su conjugado es (x + y). Entonces, el producto de los dos binomios es la diferencia de los cuadrados de los términos:
(x – y).(x + y) = x2 – y2
Índice del artículo
La regla enunciada de los binomios conjugados es la siguiente:
El producto de dos binomios conjugados es igual al cuadrado del primer término menos el cuadrado del segundo término. A este resultado se le llama diferencia de cuadrados.
A modo de ejemplo de aplicación, comenzaremos por demostrar el resultado anterior, cosa que puede realizarse usando la propiedad distributiva del producto respecto de la suma algebraica.
(x – y)(x + y) = x.x + x.y – y.x – y.y
La multiplicación anterior se obtuvo siguiendo estos pasos:
– Se multiplica el primer término del primer binomio por el primer término del segundo
– Luego el primero del primero, por el segundo del segundo
– Seguidamente el segundo del primero por el primero del segundo
– Finalmente el segundo del primero por el segundo del segundo.
Ahora hagamos un pequeño cambio usando la propiedad conmutativa: y.x = x.y. Queda así:
(x – y)(x + y) = x.x + x.y – x.y – y.y
Como hay dos términos iguales pero de signo contrario (resaltados en color y subrayados), se cancelan y se simplifica:
(x – y)(x + y) = x.x – y.y
Por último se aplica que multiplicar un número por sí mismo, equivale a elevarlo al cuadrado, por lo que x.x = x2 y también y.y = y2.
De esta forma queda demostrado lo que se había señalado en la sección precedente, que el producto de una suma por su diferencia, es la diferencia de los cuadrados:
(x – y).(x + y) = x2 – y2
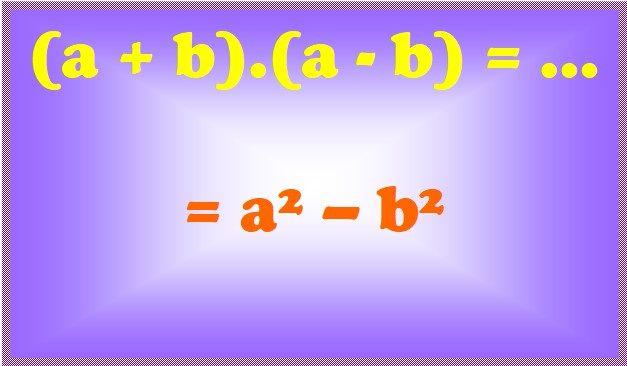
Ejemplo 1
Encuentre el conjugado de (y2 – 3y).
Respuesta: (y2 + 3y)
Ejemplo 2
Obtenga el producto de (y2 – 3y) por su conjugado.
Respuesta: (y2 – 3y)(y2 + 3y) = (y2)2 – (3y)2 = y4 – 32 y2 = y4 – 9y2
Ejemplo 3
Desarrolle el producto (1 + 2a).(2a -1).
Respuesta: la expresión anterior es equivalente a (2a + 1).(2a -1), es decir corresponde al producto de un binomio por su conjugado.
Se sabe que el producto de un binomio por su binomio conjugado es igual a la diferencia de los cuadrados de los términos del binomio:
(2a + 1)(2a -1) = (2a)2 – 12 = 4 a2 – 1
Ejemplo 4
Escriba el producto (x + y + z)(x – y – z) como una diferencia de cuadrados.
Respuesta: podemos asimilar los trinomios anteriores a la forma de binomios conjugados, haciendo uso cuidadoso de los paréntesis y corchetes:
(x + y + z)(x – y – z)=[x + (y+z)][x – (y+z)]
De esta manera se puede aplicar la diferencia de cuadrados:
(x + y + z)(x – y – z) = [x + (y+z)].[x – (y+z)] = x2 – (y+z)2
Ejemplo 5
Exprese el producto (m2 – m -1).(m2 + m -1) como una diferencia de cuadrados.
Respuesta: la expresión anterior es el producto de dos trinomios. En primer lugar debe reescribirse como el producto de dos binomios conjugados:
(m2 – m -1)(m2 + m -1) = (m2 – 1 – m)(m2 -1 + m) = [(m2 -1) – m].[(m2 -1) +m)]
Aplicamos el hecho de que el producto de un binomio por su conjugado es la diferencia cuadrática de sus términos, tal como se ha explicado:
[(m2 -1) – m].[(m2 -1) +m)] = (m2 -1)2 – m2
Como siempre, se comienza por los ejercicios más sencillos y luego se va elevando el nivel de complejidad.
Escriba (9 – a2) como un producto.
Solución
En primer lugar, reescribimos la expresión como una diferencia de cuadrados, con la finalidad de aplicar lo explicado previamente. Por lo tanto:
(9 – a2)=(32 – a2)
Enseguida factorizamos, lo cual equivale a escribir esta diferencia de cuadrados como un producto, tal como se pide en el enunciado:
(9 – a2)=(32 – a2)=(3 + a)(3 -a)
Factorize 16x2 – 9y4.
Solución
Factorizar una expresión significa escribirla como un producto. En este caso, es preciso reescribir previamente la expresión, para obtener una diferencia de cuadrados.
No es difícil hacerlo, ya que observando con cuidado, todos los factores son cuadrados perfectos. Por ejemplo 16 es el cuadrado de 4, 9 es el cuadrado de 3, y4 es el cuadrado de y2 y x2 es el cuadrado de x:
16x2 – 9y4 = 42x2 – 32y4 = 42x2 – 32(y2)2
Luego se aplica lo que ya sabemos previamente: que una diferencia de cuadrados es el producto de binomios conjugados:
(4x)2 – (3 y2)2 = (4x – 3 y2) . (4x + 3 y2)
Escriba (a – b) como producto de binomios
Solución
La diferencia anterior debe escribirse como diferencias de cuadrados
(√a)2 -(√b)2
Luego se aplica que la diferencia de cuadrados es el producto de los binomios conjugados
(√a – √b)(√a + √b)
Uno de los usos del binomio conjugado es la racionalización de expresiones algebraicas. Este procedimiento consiste en eliminar las raíces del denominador de una expresión fraccionaria, que en numerosas ocasiones facilita las operaciones. Se pide usar el binomio conjugado para racionalizar la siguiente expresión:
√(2-x) / [√3 – √(2+x)]
Solución
Lo primero es identificar el binomio conjugado del denominador: [√3 + √(2+x)].
Ahora multiplicamos numerador y denominador de la expresión original por el binomio conjugado:
√(2-x) [√3 + √(2+x)] /{[√3 – √(2+x)].[√3 + √(2+x)]}
En el denominador de la expresión anterior reconocemos el producto de una diferencia por una suma, que ya sabemos que corresponde a la diferencia de los cuadrados de los binomios:
√(2-x) .[√3 + √(2+x)] /{(√3)2 – [√(2+x)]2 }
Simplificando el denominador queda:
√(2-x).[√3 + √(2+x)] / [3 – (2+x)] = √(2-x). [√3 + √(2+x)] / (1 – x)
Ahora nos ocupamos del numerador, para lo cual aplicaremos la propiedad distributiva del producto respecto de la suma:
√(2-x) .[√3 + √(2+x)] / (1 – x )= √(6-3x) + √[(2-x)(2+x)] / (1 – x)
En la expresión anterior reconocemos el producto del binomio (2-x) por su conjugado, el cual es el producto notable igual a la diferencia de cuadrados. De esta manera se obtiene finalmente una expresión racionalizada y simplificada:
[√(6-3x) + √(4-x2)] / (1 – x)
Desarrolle el siguiente producto, usando las propiedades del binomio conjugado:
[2a(x + 3y) – 3a(x – 3y)].[2a(x + 3y) + 3a(x – 3y)]
Solución
4a(2x + 6y) – 9a(2x – 6y) = 4a(2x) .a(6y) – 9a(2x) .a(-6y)= [4a(6y) – 9a(-6y)] .a(2x)
El lector atento se habrá percatado del factor común que se ha resaltado en color.
- Baldor, A. 1991. Álgebra. Editorial Cultural Venezolana S.A.
- González J. Ejercicios de binomios conjugados. Recuperado de: academia.edu.
- Matemáticas profe Alex. Productos Notables. Recuperado de youtube.com.
- Math2me. Binomios conjugados/ productos notables. Recuperado de youtube.com.
- Productos de binomios conjugados. Recuperado de: lms.colbachenlinea.mx.
- Vitual. Binomios conjugados. Recuperado de: youtube.com.
