Teorema de Thévenin: en qué consiste, aplicaciones y ejemplos
El teorema de Thévenin afirma que un circuito con terminales A y B puede ser sustituido por uno equivalente que conste de una fuente y una resistencia en serie, cuyos valores dan la misma diferencia de potencial entre A y B y la misma impedancia que el circuito original.
Este teorema fue dado a conocer en el año 1883 por el ingeniero francés Léon Charles Thévenin, pero se afirma que fue enunciado treinta años antes por el físico alemán Hermann von Helmholtz.
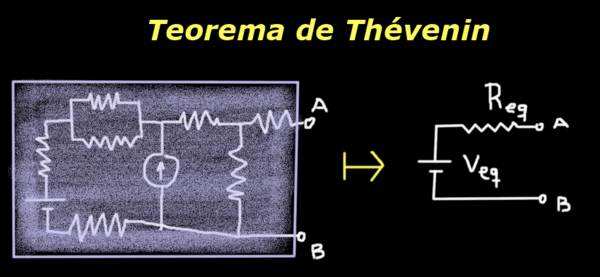
Su utilidad radica en el hecho de que, aun cuando el circuito original sea complejo o desconocido, para efectos de una carga o impedancia que se coloque entre los terminales A y B, el sencillo circuito equivalente de Thévenin se comporta de idéntica manera que el original.
Índice del artículo
- 1 ¿Como se calcula la tensión equivalente paso a paso?
- 2 Aplicaciones del teorema de Thévenin (parte I)
- 3 Comprobación del teorema de Thévenin
- 4 Aplicación del teorema de Thévenin (parte II)
- 5 Aplicación del teorema de Thévenin (parte III)
- 6 Referencias
La tensión o diferencia de potencial del circuito equivalente puede obtenerse de las siguientes maneras:
Obtención del voltaje equivalente de Thévenin
Si se trata de un aparato o equipo que está en una “caja negra” se procede a medir la diferencia de potencial entre las terminales A y B con un voltímetro o con un osciloscopio. Es muy importante que no se coloque ninguna carga o impedancia entre las terminales A y B.
Un voltímetro o un osciloscopio no representan ninguna carga para las terminales, ya que ambos equipos tienen una impedancia muy grande (idealmente infinita) y sería como si las terminales A y B estuviesen sin carga. El voltaje o tensión obtenida de esta manera es la tensión equivalente de Thévenin.
Obtención de la impedancia equivalente de Thévenin
Para obtener la impedancia equivalente a partir de una medición experimental se coloca una resistencia conocida entre las terminales A y B y se mide la caída de tensión o la señal de voltaje con un osciloscopio.
A partir de la caída de tensión en la resistencia conocida entre las terminales, puede obtenerse la corriente que circula a través de la misma.
El producto de la corriente obtenida con la resistencia equivalente más la caída de tensión medida en la resistencia conocida es igual al voltaje equivalente de Thévenin previamente obtenido. De esta igualdad se despeja la impedancia equivalente de Thévenin.
Cálculo del voltaje equivalente de Thévenin
En primer lugar se desconecta toda carga o impedancia de las terminales A y B.
Como se conoce el circuito se aplica la teoría de mallas o las leyes de Kirchhoff para encontrar la tensión en las terminales. Esta tensión será la equivalente de Thévenin.
Cálculo de la impedancia equivalente de Thévenin
Para obtener la impedancia equivalente se procede a:
– Sustituir las fuentes de voltaje del circuito original por cortocircuitos “impedancia cero” y las fuentes de corriente del circuito original por abiertos “impedancia infinita”.
– Luego se calcula la impedancia equivalente siguiendo las reglas de impedancias en serie e impedancias en paralelo.
Aplicaremos el teorema de Thévenin para resolver algunos circuitos. En esta primera parte consideramos un circuito que solo posee fuentes de tensión y resistencias.
La figura 2 muestra el circuito que está en un recuadro celeste el cual tiene dos baterías de fuerza electromotriz V1 y V2 respectivamente y las resistencias R1 y R2, el circuito tiene terminales A y B en los cuales puede conectarse una carga.
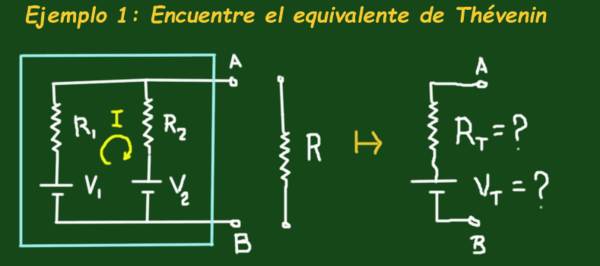
El objetivo es encontrar el circuito equivalente de Thévenin, es decir, determinar los valores Vt y Rt del circuito equivalente. Aplique los siguientes valores: V1= 4V, V2=1V, R1=3Ω, R2=6Ω y R=1Ω.
Solución paso a paso
Paso 1
Determinaremos la tensión en los terminales A y B cuando no se les coloca carga alguna.
Paso 2
El circuito a resolver consta de una única malla por la que circula una corriente I que la hemos tomado positiva en el sentido horario.
Paso 3
Recorremos la malla comenzando con la esquina inferior izquierda. El recorrido conduce a la siguiente ecuación:
V1 – I*R1 – I*R2 – V2 = 0
Paso 4
Despejamos la corriente de malla I y obtenemos:
I = (V1 -V2)/(R1+R2) = (4V – 1V) / (3Ω +6Ω) = ⅓ A
Paso 5
Con la corriente de malla podemos determinar la diferencia de tensión o voltaje entre A y B, la cual es:
Vab = V1 – I*R1 = 4V – ⅓ A * 3Ω = 3V
Es decir que el voltaje equivalente de Thevenin es: Vt = 3V.
Paso 6 (Resistencia equivalente de Thévenin)
Procedemos ahora a calcular la resistencia equivalente de Thévenin, para lo cual y según se había dicho anteriormente, se sustituyen las fuentes de voltaje por un cable.
En ese caso, solo tenemos dos resistencias en paralelo, por lo que la resistencia equivalente de Thévenin es:
Rt = (R1 * R2) / (R1 + R2) = ( 3Ω * 6Ω ) / ( 3Ω + 6Ω ) = 2Ω
Conectar como carga a las terminales A y B una resistencia R=1Ω al circuito equivalente y encontrar la corriente que circula por dicha carga.
Solución
Cuando se conecta la resistencia R al circuito equivalente de Thevenin se tiene un circuito simple que consta de una fuente Vt una resistencia Rt en serie con la resistencia R.
Llamaremos Ic a la corriente que circula por la carga R, de modo que la ecuación de malla queda así:
Vt – Ic* Rt – Ic* R = 0
de lo que se deduce que Ic está dado por:
Ic = Vt / (Rt + R) = 3V / ( 2Ω + 1Ω ) = 1 A
Para verificar que se cumple el teorema de Thévenin, conecte R al circuito original y encuentre la corriente que circula por R aplicando la ley de las mallas al circuito resultante.
El circuito resultante queda y sus ecuaciones de malla quedan como se muestra en la siguiente figura:
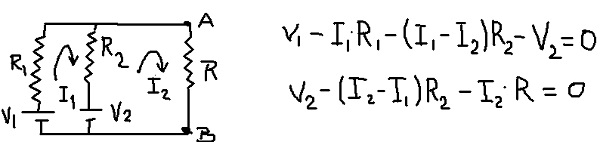
Sumando las ecuaciones de malla, es posible encontrar la corriente de malla I1 en función de la corriente I2. Luego se sustituye en la segunda ecuación de malla y queda una ecuación con I2 como única incógnita. El siguiente cuadro muestra las operaciones.
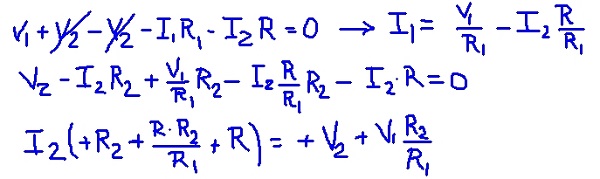
Luego se sustituyen los valores de la resistencia y voltajes de las fuentes, obteniéndose el valor numérico de la corriente de malla I2.
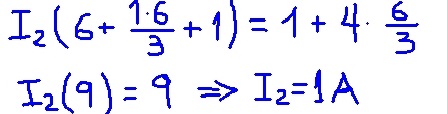
La corriente de malla I2 es la corriente que circula por la resistencia de carga R y el valor encontrado de 1 A coincide plenamente con el que fue encontrado previamente con el circuito equivalente de Thévenin.
En esta segunda parte se aplicará el teorema de Thévenin en un circuito que posee fuentes de tensión, fuente de corriente y resistencias.
El objetivo es determinar el circuito equivalente de Thévenin correspondiente al circuito de la figura siguiente, cuando los terminales están sin la resistencia de 1 ohmio, luego se coloca la resistencia y se determina la corriente circulante por la misma.
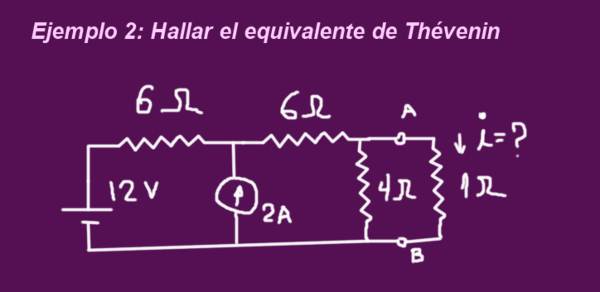
Solución
Para hallar la resistencia equivalente se retira la resistencia de carga (en este caso la de 1 ohmio). Además, las fuentes de voltaje se sustituyen por un corto circuito y las fuentes de corriente por un circuito abierto.
De este modo, el circuito al que se le calculará la resistencia equivalente es el que se muestra a continuación:
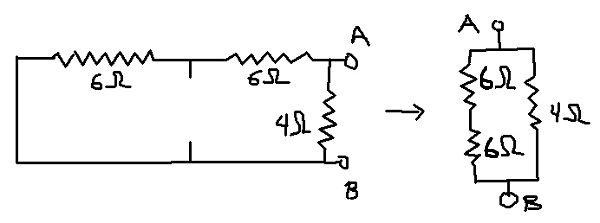
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω que es la resistencia equivalente de Thevenin (Rth).
Calcule el voltaje equivalente de Thévenin.
Solución
Para calcular el voltaje equivalente de Thévenin consideramos el circuito siguiente, en el que colocaremos las corrientes en las I1 e I2 en las ramas señaladas en la siguiente figura:
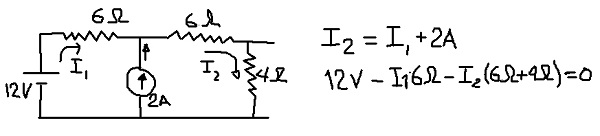
En la figura anterior se muestran la ecuación de los nodos de corriente y las ecuación de tensiones cuando se recorre la malla externa. De la segunda de las ecuaciones se despeja la corriente I1:
I1 = 2 – I2*(5/3)
Esta ecuación se sustituye en la ecuación de los nodos:
I2 = 2 – (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Esto significa que la caída de tensión en la resistencia de 4 ohmios es de 6 voltios.
En síntesis la tensión de Thévenin es Vth = 6 V.
Encontrar el circuito equivalente de Thevenin y corriente en la resistencia de carga.
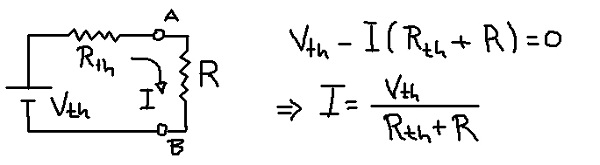
Solución
En la figura anterior se muestra el circuito equivalente de Thévenin con la resistencia de carga R. De la ecuación de tensión en la malla se deduce la corriente I que circula por la resistencia de carga R.
I = Vth / (Rth + R) = 6V / ( 3Ω + 1Ω) = 1,5 A
En esta tercera parte de aplicación del teorema de Thévenin se considera un circuito de corriente alterna que contiene una fuente de tensión alterna, un condensador, una inductancia y una resistencia.
El objetivo es encontrar el Circuito de Thévenin equivalente del siguiente circuito:
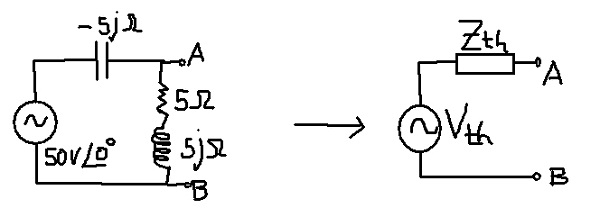
Solución
La impedancia equivalente corresponde a la del condensador en paralelo con la combinación en serie de la resistencia y la inductancia.
El inverso de la impedancia equivalente está dado por:
Zeq^-1 = (-5j)^-1 + ( 5 + 5j )^-1 = (1/5) j + ((1/10 + (1/10)j) = ( 1/10 + 3/10 j) Mho
Y la impedancia equivalente será entonces:
Zeq = (1 – 3 j) Ohm
La corriente compleja I puede deducirse de la ecuación de malla:
50V∠0 – I ( -5 j + 5 + 5j ) = 50V∠0 – I*5 = 0 ===> I = 10A ∠0
Ahora se calcula la caída de tensión en la resistencia más la inductancia, es decir la tensión Vab que será la tensión equivalente de Thévenin:
Vab = I * ( 5 + 5 j)Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Es decir que la tensión equivalente tiene el mismo valor pico de la fuente original pero está desfasada 45 grados: Vth = 50V∠45º
- Electronics tutorials, Thevenin’s theorem. Recuperado de: electronics-tutorials.ws
- Network theory questions and answers. Thevenin’s theorem. Recobrado de: sanfoundry.com
- Thevenin’s theorem. Step by step procedure. Recuperado de: electricaltechnology.org
- Thevenin’s theorem. Solved example step by step. Recuperado de: electricalsimple.blogspot.com
- Workshop on Thevenin’s and Norton’s theorems. Recuperado de: web.iit.edu
- Wikipedia. Teorema de Thévenin. Recuperado de: wikipedia.com
