¿Qué es el rango en estadística? (Con ejemplos)

El rango, recorrido o amplitud, en estadística, es la diferencia (resta) entre el valor máximo y el valor mínimo de un conjunto de datos provenientes de una muestra o de una población. Si se representa al rango con la letra R y a los datos mediante x, la fórmula para el rango es simplemente:

R = x_máx – x_mín

 Donde x_máx es el valor máximo de los datos y x_min es el mínimo.

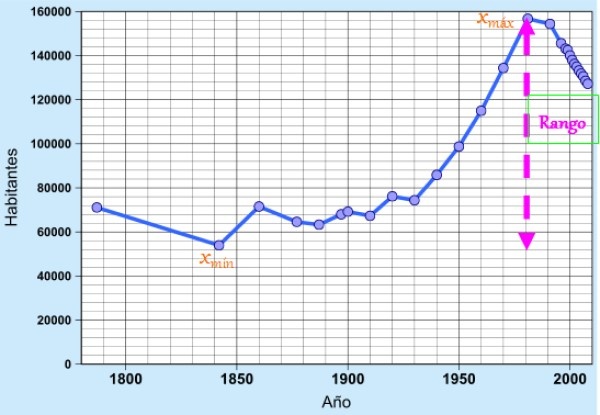
El concepto es muy útil como medida de dispersión sencilla para apreciar rápidamente la variabilidad de los datos, pues indica la extensión o longitud del intervalo donde se hallan estos.

Por ejemplo, supongamos que se mide la estatura de un grupo de 25 estudiantes varones del primer año de ingeniería en una universidad. El estudiante más alto del grupo mide 1.93 m y el más bajo 1.67 m. Estos son los valores extremos de los datos de la muestra, por lo tanto el recorrido de los mismos es:

R = 1.93 – 1.67 m = 0.26 m o 26 cm.

La estatura de los alumnos de este grupo se distribuye a lo largo de este rango.

Índice del artículo

• 1 Ventajas y desventajas
  • 1.1 Desventajas del rango como medida de dispersión
• 2 Recorrido intercuartil, cuartiles y ejemplo resuelto
  • 2.1 – Cálculo de los cuartiles
• 3 Ejemplo resuelto
• 4 Referencias

Ventajas y desventajas

El rango es, como dijimos antes, una medida de cuán dispersos están los datos. Un rango pequeño indica que los datos están más o menos cercanos y la dispersión es poca. En cambio un rango mayor es indicativo que los datos están más dispersos.

Las ventajas de calcular el rango son evidentes: es muy sencillo y rápido de hallar, pues es una simple diferencia.

Además tiene las mismas unidades que los datos con los cuales se trabaja y el concepto es muy fácil de interpretar para cualquier observador.

En el ejemplo de la estatura de los estudiantes de ingeniería, si el rango hubiera sido de 5 cm, diríamos que los alumnos son todos aproximadamente del mismo tamaño. Pero con un rango de 26 cm, suponemos de inmediato que en la muestra hay alumnos de todas las estaturas intermedias. ¿Siempre se acierta con esta suposición?

Desventajas del rango como medida de dispersión

Si nos fijamos con cuidado, puede que en nuestra muestra de 25 estudiantes de ingeniería, solamente uno de ellos mide 1.93 y los restantes 24 tienen estaturas cercanas a 1.67 m.

Y sin embargo el rango sigue siendo el mismo, aunque es perfectamente posible que ocurra lo contrario: que la estatura de la mayoría oscile alrededor del 1.90 m y solamente uno mide 1.67 m.

En cualquiera de los casos, la distribución de los datos es bien diferente.

Las desventajas del rango como medida de dispersión se deben a que solamente usa los valores extremos e ignora todos los demás. Como la mayor parte de la información se pierde, no se tiene idea de cómo se distribuyen los datos de la muestra.

Otra característica importante es que el rango de la muestra nunca disminuye. Si añadimos más información, es decir, consideramos más datos, el rango aumenta o se queda igual.

Y en todo caso, es útil solamente cuando se trabaja con muestras pequeñas, no siendo recomendable su uso único como medida de dispersión en muestras grandes.

Lo que hay que hacer es complementar con el cálculo de otras medidas de dispersión que sí tengan en cuenta la información que suministra el total de los datos: recorrido intercuartílico, varianza, desviación estándar y coeficiente de variación.

Recorrido intercuartil, cuartiles y ejemplo resuelto

Nos hemos dado cuenta de que la debilidad del rango como medida de dispersión radica en que solamente hace uso de los valores extremos de la distribución de los datos, omitiendo los demás.

Para evitar este inconveniente se usan los cuartiles: tres valores conocidos como medidas de posición.

Ellas distribuyen los datos no agrupados en cuatro partes (otras medidas de posición muy utilizadas son los deciles y los percentiles). Estas son sus características:

-El primer cuartil Q₁ es el valor de los datos tal que el 25 % de todos ellos es menor que Q₁.

-El segundo cuartil Q₂ es la mediana de la distribución, lo cual quiere decir que la mitad (50 %) de los datos es menor a dicho valor.

-Finalmente el tercer cuartil Q₃ señala que el 75 % de los datos son menores a Q₃.

Entonces, se define el rango intercuartil o recorrido intercuartílico como la diferencia entre el tercer cuartil Q₃ y el primer cuartil Q₁ de los datos:

Recorrido intercuartil = R_Q = Q₃ – Q₁

De esta forma, el valor del rango R_Q no resulta tan afectado por los valores extremos. Por ello es recomendable usarlo cuando se trata de distribuciones sesgadas, como podrían serlo las de los alumnos muy altos o muy bajos descritas anteriormente.

– Cálculo de los cuartiles

Hay varias maneras de calcularlos, aquí propondremos una, pero en todo caso es necesario saber el número de orden “N_o”, que es el lugar que ocupa el respectivo cuartil en la distribución.

Es decir, si por ejemplo el término que corresponde a Q₁ es el segundo, el tercero o el cuarto y así sucesivamente de la distribución.

Primer cuartil

N_o (Q₁) =  (N+1) / 4

Segundo cuartil o mediana

N_o (Q₂) =  (N+1) / 2

Tercer cuartil

N_o (Q₃) =  3(N+1) / 4

Donde N es el número de datos.

La mediana es el valor que está justo en medio de la distribución. Si el número de datos es impar no hay problema en encontrarla, pero si es par, entonces se promedian los dos valores centrales para convertirlos en uno solo.

Una vez calculado el número de orden se sigue alguna de estas tres reglas:

-Si no tiene decimales, se busca el dato indicado en la distribución y este será el cuartil buscado.

-Cuando el número de orden está a mitad de camino entre dos, entonces se promedia el dato indicado por la parte entera con el dato siguiente, y el resultado es el cuartil correspondiente.

-En cualquier otro caso, se redondea al entero más cercano y esa será la posición del cuartil.

Ejemplo resuelto

En una escala del 0 al 20, un grupo de 16 estudiantes de matemáticas I obtuvo las siguientes calificaciones (puntos) en un examen parcial:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Encontrar:

a) El rango o recorrido de los datos.

b) Los valores de los cuartiles Q₁ y Q₃

c) El rango intercuartil.

Solución a

Lo primero que hay de hacer para encontrar el recorrido es ordenar los datos de forma creciente o decreciente. Por ejemplo en orden creciente se tiene:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Mediante la fórmula dada al comienzo: R = x_máx – x_mín

R = 20 – 1  puntos = 19 puntos.

De acuerdo al resultado, estas calificaciones tienen una gran dispersión.

Solución b

N = 16

N_o (Q₁) =  (N+1) / 4 = (16 + 1) / 4 = 17 / 4 = 4.25

Es un número con decimales, cuya parte entera es 4. Entonces vamos a la distribución, se busca el dato que ocupa el cuarto lugar y se promedia su valor con el de la quinta posición. Como ambos son 9, el promedio también es 9 y entonces:

Q₁ = 9

Ahora repetimos el procedimiento para hallar Q₃:

N_o (Q₃) =  3(N+1) / 4 = 3 (16 +1)/4 = 12.75

Nuevamente es un decimal, pero como no está a mitad de camino se redondea a 13. El cuartil buscado ocupa la treceava posición y es:

Q₃ = 16

Solución c

R_Q = Q₃ – Q₁ = 16 – 9 = 7 puntos.

Que como vemos es mucho menor que el rango de datos calculado en el apartado a), porque la calificación mínima fue de 1 punto, un  valor bastante más alejado del resto.

Referencias

1. Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
2. Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
3. Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
4. Ejemplos de cuartiles. Recuperado de: matematicas10.net.
5. Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
6. Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.