Diferencia entre círculo y circunferencia (con ejemplos)
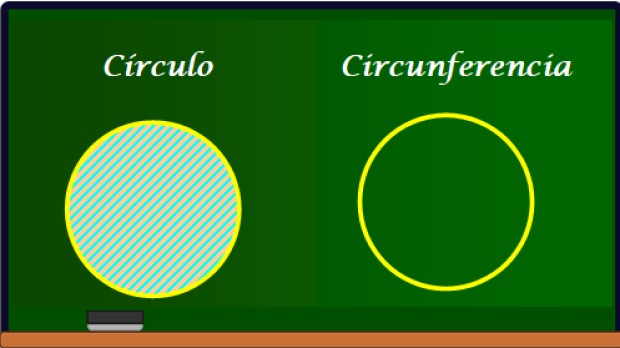
La diferencia entre círculo y circunferencia es la siguiente: el círculo es una superficie plana, contorneada o delimitada por una circunferencia, mientras que esta última es una curva plana.
Con frecuencia ambos conceptos se confunden, ya que están relacionados, pero siempre hay que recordar que la circunferencia es el borde del círculo, mientras que este contiene a la circunferencia y a todos los puntos interiores a ella.
Ambos tienen muchos elementos en común, como por ejemplo el centro, el radio y el diámetro, entre otros, según la siguiente tabla comparativa:
Círculo | Circunferencia | |
Definición | Figura geométrica plana, cuyo contorno es una circunferencia. | Curva cerrada y plana, formada por todos los puntos que equidistan del centro. |
Elementos y regiones |
|
|
Fórmulas | Perímetro: P=2π⋅r | Longitud: L=2π⋅r |
Índice del artículo
- 1 Círculo: definición, características y partes
- 2 Circunferencia: definición, características y partes
- 3 Referencias
Un círculo es una figura geométrica plana, la cual incluye todos los puntos de la circunferencia que forma el contorno y también todos los puntos interiores.
Por tal motivo se caracteriza por tener:
-Borde o perímetro, que es la circunferencia del círculo.
-Un área superficial.
Todo círculo posee las siguientes partes o elementos:
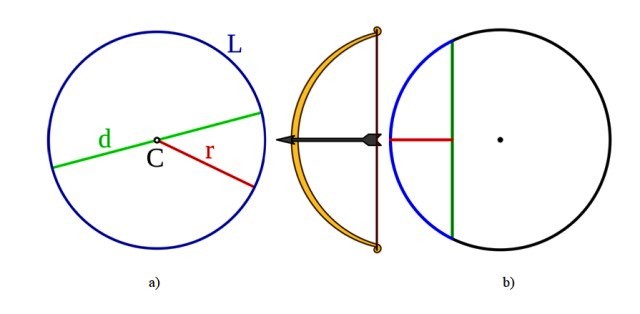
Centro: que es el punto C, del cual equidistan todos los puntos del borde.
Cuerda: segmento que une dos puntos del borde del círculo. En la figura b) de la derecha, es el segmento en verde más oscuro.
Diámetro: segmento de color verde más claro, denotado “d” en la figura a), que une dos puntos del borde y que a la vez pasa por el centro. El diámetro también es una cuerda, la más larga de todas, por eso se la conoce como la cuerda mayor.
Radio: denotado mediante “r” en la figura a), es el segmento rojo que une el centro del círculo con un punto del borde. Su medida es la mitad del diámetro.
Arco: una porción del contorno que se encuentra entre dos puntos de este, en azul en la figura b).
Ángulo central: es el ángulo cuyo vértice está en el centro O y los lados son radios del círculo.
Flecha: segmento perpendicular a una cuerda (en rojo en la figura b), que une el centro de la cuerda con un punto del borde.
Longitud o perímetro: es la medida del contorno del círculo, denotado L. Depende del radio r y es proporcional al número irracional π:
π = 3.1416…
De manera que:
L=2π⋅r
Al ser una figura plana, el círculo tiene un área total y también diversas regiones. Las más conocidas son las siguientes:
Área del círculo: es proporcional al cuadrado del radio, siendo la constante de proporcionalidad el número π.
Llamando A al área del círculo, queda expresada como:
A = πr2
Segmento circular: es una porción del círculo limitada por el arco de color azul y la cuerda verde oscuro en la figura b.
Sector circular: también es una región del círculo, pero contenida entre dos radios y el arco correspondiente.
Corona circular: tiene forma de un anillo y está limitada por dos circunferencias concéntricas, por fuera de la de radio menor y por dentro de la radio mayor.
La circunferencia es el borde del círculo y por lo tanto tiene muchos elementos en común con este. Sin embargo, la circunferencia no tiene área, porque al tratarse de una curva solamente tiene longitud L.
Se define formalmente la circunferencia como el conjunto de todos los puntos que equidistan de otro punto conocido como el centro.
No se incluyen los puntos interiores, ya que estos corresponden al círculo.

Muchos de los elementos de la circunferencia son los mismos que los del círculo, excluyendo los que se refieren a áreas y regiones, por ello la figura superior vuelve a servir como referencia.
Tenemos entonces:
Centro: denotado mediante C y a veces también como O, todos los puntos de la circunferencia guardan la misma distancia con él.
Cuerda: segmento que une dos puntos pertenecientes a la circunferencia.
Diámetro: también une dos puntos de la circunferencia, pero siempre pasa por el centro de la misma.
Radio: es la distancia entre el centro y cualquier punto de la circunferencia.
Arco: es una porción de la circunferencia.
Ángulo central: es el ángulo con el vértice en el centro C y dos lados iguales que miden igual que el radio.
Flecha: segmento perpendicular a una cuerda, que une el centro de esta con el correspondiente punto de la circunferencia.
Longitud o perímetro: es la medida de la circunferencia, que como hemos visto, es proporcional al número π = 3.1416… y se calcula mediante la fórmula:
L=2π⋅r
Un punto P pertenece a una circunferencia siempre y cuando su distancia a otro punto C sea igual a r, el radio.
Cualquier punto en el plano cartesiano tiene coordenadas (x,y) y el cuadrado de la distancia d entre dos de ellos, P1(x1,y1) y P2(x2,y2), viene dada por la fórmula:
d22 = (x2 – x1)2 + (y2 – y1)2
Tomemos entonces al punto P de coordenadas (x,y) y al punto C de coordenadas (h,k). Sustituyendo, la ecuación anterior quedaría así:
(x – h)2 + (y– k)2 = r2
Esta es la ecuación de la circunferencia, que cualquier punto sobre ella satisface. Si el centro de la circunferencia se hace coincidir con el origen del sistema de coordenadas, entonces h = k = 0 y la ecuación se simplifica a:
x2 + y2 = r2
Veamos un ejemplo de cómo usar la ecuación y responder esta cuestión: ¿pertenece el punto (4,6) a la circunferencia (x – 1)2 + (y – 2)2 = 25?
Para averiguarlo se sustituyen las coordenadas del punto en la ecuación, y si resulta una igualdad, entonces el punto sí pertenece a la circunferencia:
(4 – 1)2 + (6 – 2)2 = 32 + 42 = 9 + 16 = 25
Y efectivamente, como 25 = 25, se concluye que (4,6) sí pertenece a la circunferencia.
- Free Mathematics Tutorials. Area and Perimeter of a Circle – Geometry Calculator. Recuperado de: analyzemath.com.
- Math Open Reference. Circumference, Perimeter of a circle. Recuperado de: mathopenref.com.
- Sciencing. How to find the Perimeter of a Circle. Recuperado de: sciencing.com.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
