Onda senoidal: características, partes, cálculo, ejemplos
Las ondas senoidales son patrones de ondas que matemáticamente pueden ser descritas mediante las funciones seno y coseno. Describen acertadamente eventos naturales y señales variables en el tiempo, tales como los voltajes generados por centrales eléctricas y luego utilizados en hogares, industrias y calles.
Elementos eléctricos como resistencias, condensadores e inductancias, que se conectan a entradas de voltaje sinusoidal, producen respuestas también sinusoidales. Las matemáticas que se utilizan en su descripción son relativamente sencillas y han sido minuciosamente estudiadas.
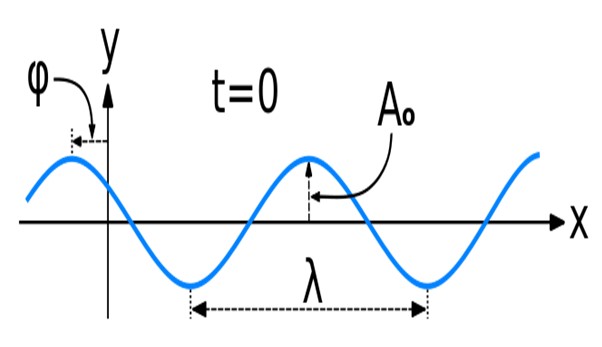
La matemática de las ondas senoidales o sinusoidales, como también se las conoce, es la de las funciones seno y coseno.
Se trata de funciones repetitivas, lo que significa periodicidad. Ambas tienen idéntica forma, con la salvedad de que el coseno está desplazado hacia la izquierda respecto al seno en un cuarto de ciclo. Se observa en la figura 2:
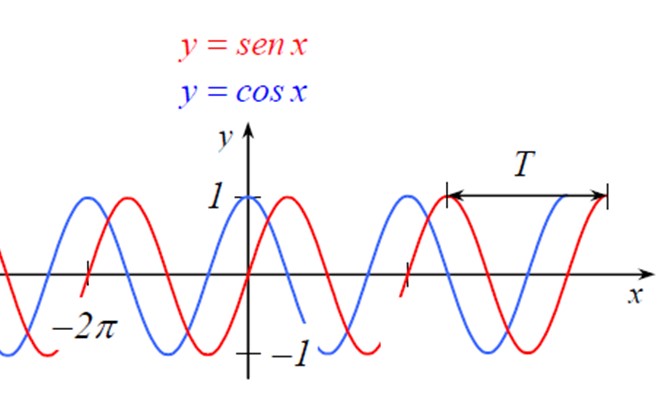
Entonces cos x = sen (x + π/2). Con ayuda de estas funciones se representa una onda senoidal. Para ello, en el eje vertical se coloca la magnitud en cuestión, mientras que en el eje horizontal se ubica el tiempo.
En la gráfica de arriba también se aprecia la cualidad repetitiva de estas funciones: el patrón se repite continua y regularmente. Gracias a estas funciones se pueden expresar voltajes y corrientes de tipo senoidal variando en el tiempo, colocando en el eje vertical en vez de la y, una v o una i para representar voltaje o corriente, y en el eje horizontal en vez de la x, se coloca la t del tiempo.
La forma más general para expresar una onda senoidal es:
v (t) = vm sen (ωt+φ)
Seguidamente profundizaremos en el significado de esta expresión, definiendo algunos términos básicos con la finalidad de caracterizar la onda senoidal.
Índice del artículo
Período, amplitud, frecuencia, ciclo y fase son conceptos se aplican a las ondas periódicas o repetitivas y son importantes para caracterizarlas adecuadamente.
Una función periódica como las mencionadas, la cual se repite a intervalos regulares, cumple siempre la siguiente propiedad:
f (t) = f (t+ T) = f (t + 2T) = f (t + 3T) = ….
Donde T es una cantidad denominada período de la onda, y es el tiempo que tarda en repetirse una fase de la misma. En unidades de Sistema Internacional, el período se mide en segundos.
De acuerdo a la expresión general de la onda senoidal v (t) = vm sen (ωt+φ), vm es el valor máximo de la función, que ocurre cuando sen (ωt+φ)= 1 (recordando que el mayor valor que admite tanto la función seno como la función coseno es 1). Este valor máximo es justamente la amplitud de la onda, también conocida como amplitud pico.
En caso de tratarse de un voltaje se medirá en Voltios y si es una corriente será en Amperios. En la onda senoidal mostrada la amplitud es constante, pero en otros tipos de onda la amplitud puede variar.
Es una parte de la onda contenida en un período. En la figura anterior se tomó el período midiéndolo desde dos cimas o crestas consecutivas, pero puede comenzar a medirse desde otros puntos de la onda, mientras estén limitados por un período.
Obsérvese en la siguiente figura como un ciclo abarca desde un punto hasta otro con el mismo valor (altura) y la misma pendiente (inclinación).
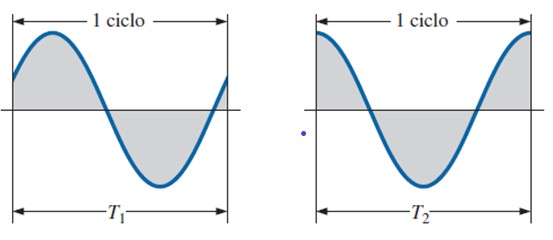
Es la cantidad de ciclos que ocurren en 1 segundo y se encuentra vinculada al argumento de la función seno: ωt. La frecuencia se denota como f y se mide en ciclos por segundo o Hertz (Hz) en Sistema Internacional.
La frecuencia es la cantidad inversa del período, por lo tanto:
f = 1/T
Mientras que la frecuencia f está relacionada con la frecuencia angular ω (pulsación) como:
ω = 2πf
La frecuencia angular se expresa en radianes /segundo en el Sistema Internacional, pero los radianes son adimensionales, así la frecuencia f y la frecuencia angular ω tienen las mismas dimensiones. Obsérvese que el producto ωt da radianes como resultado, debiendo tenerse en cuenta a la hora de utilizar la calculadora para obtener el valor de sen ωt.
Se corresponde al desplazamiento horizontal experimentado por la onda, respecto a un tiempo tomado como referencia.
En la siguiente figura la onda verde está adelantada respecto a la roja en un tiempo td. Dos ondas sinusoidales están en fase cuando su frecuencia y su fase son las mismas. Si la fase difiere, entonces están en desfase. Las ondas de la figura 2 también están desfasadas.
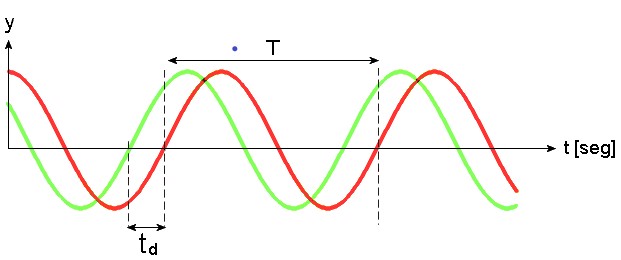
Si la frecuencia de las ondas es diferente, estarán en fase cuando la fase ωt+φ sea la misma en ambas ondas en determinados instantes.
Hay muchas formas de obtener una señal en forma de onda senoidal. Las tomas de corriente caseras las proporcionan.
Una forma bastante simple de obtener una señal senoidal es haciendo uso de la ley de Faraday. Esta indica que en un circuito cerrado de corriente, por ejemplo una espira, colocado en medio de un campo magnético, se genera una corriente inducida cuando el flujo de campo magnético a través de ella cambia en el tiempo. En consecuencia se genera igualmente un voltaje inducido o fem inducida.
El flujo del campo magnético varía si la espira se hace girar con rapidez angular constante en medio del campo creado entre los polos N y S del imán mostrado en la figura.
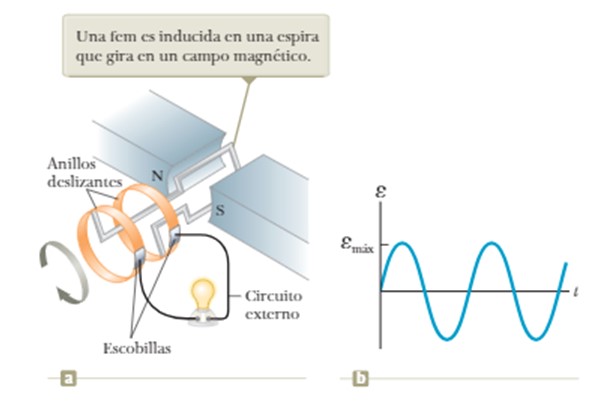
La limitación de este dispositiva es la dependencia que tiene el voltaje obtenido con la frecuencia de rotación de la espira, como se verá con mayor detalle en el ejemplo 1 de la sección de ejemplos más adelante.
Otra forma de obtener una onda senoidal, esta vez con electrónica, es mediante el oscilador de Wien, que requiere de un amplificador operacional en conexión con resistencias y condensadores. De esta forma se obtienen ondas senoidales cuya frecuencia y amplitud el usuario puede modificar según su conveniencia, mediante el ajuste con interruptores.
En la figura se muestra un generador de señales senoidales, con el cual también se pueden obtener otras formas de onda: triangulares y cuadradas entre otras.

Para realizar cálculos que involucren ondas senoidales se utiliza una calculadora científica que disponga de las funciones trigonométricas seno y coseno, así como sus inversas. Estas calculadoras disponen de modos para trabajar los ángulos ya sea en grados o en radianes, y es sencillo convertir de una forma a la otra. El factor de conversión es:
180 º = π radianes.
Según el modelo de la calculadora, deberá navegar mediante la tecla MODE para encontrar la opción DEGREE, que permite trabajar las funciones trigonométricas en grados, o bien la opción RAD, para trabajar directamente los ángulos en radianes.
Por ejemplo sen 25 º = 0.4226 con la calculadora puesta en modo DEG. Al convertir 25 º a radianes se obtiene 0.4363 radianes y sen 0.4363 rad = 0.425889 ≈ 0.4226.
El osciloscopio es un aparato que permite visualizar en una pantalla señales de voltajes y corrientes tanto alternas como directas. Tiene perillas para ajustar el tamaño de la señal sobre una cuadrícula como se muestra en la siguiente figura:
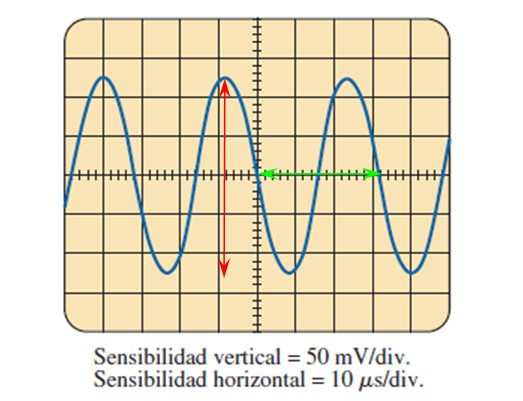
A través de la imagen que provee el osciloscopio y conociendo el ajuste de la sensibilidad en ambos ejes, es posible calcular los parámetros de la onda que se describieron anteriormente.
En la figura se muestra la señal de voltaje senoidal en función del tiempo, en la cual cada división del eje vertical vale 50 milivoltios, mientras que en el eje horizontal, cada división vale 10 microsegundos.
La amplitud pico a pico se encuentra contando las divisiones que abarca la onda en lo vertical, ayudándose con la flecha roja:
Se cuentan 5 divisiones con ayuda de la flecha roja, entonces el voltaje pico-pico es:
Vpp = 5 divisiones x 50 mV/división = 250 mV.
El voltaje pico Vp se mide a partir del eje horizontal, siendo de 125 mV.
Para encontrar el período se mide un ciclo, por ejemplo el delimitado por la flecha verde, que abarca 3.2 divisiones, entonces el período es:
T = 3.2 divisiones x 10 microsegundos/división = 32 microsegundos = 32 μs
Para el generador de la figura 3, demuestre a partir de la ley de Faraday que el voltaje inducido tiene forma senoidal. Suponga que la espira consta de N vueltas en vez de una sola, todas con la misma área A y está girando con rapidez angular constante ω en medio de un campo magnético B uniforme.
Solución
La ley de Faraday dice que la fem inducida ε es:
ε = -N(dΦB /dt)
Donde ΦB es el flujo del campo magnético, que será variable, ya que depende de cómo la espira se expone a cada instante al campo. El signo negativo simplemente describe el hecho de que esta fem se opone a la causa que la produce (ley de Lenz). El flujo debido a una sola espira es:
ΦB = B.A.cos θ
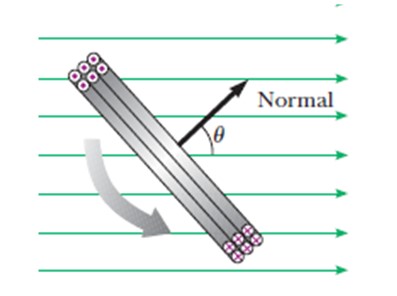
θ es el ángulo que el vector normal al plano de la espira va formando con el campo B a medida que transcurre la rotación (ver figura), este ángulo naturalmente va variando como:
θ = ωt
De manera que: ΦB = B.A.cos θ = B.A.cos ωt. Ahora solamente hay que derivar con respecto al tiempo esta expresión y con ello se obtiene la fem inducida:
ε = -N.d (B.A.cos ωt) /dt
Como el campo B es uniforme y el área de la espira no varía, salen fuera de la derivada:
ε = -NBA. d(cos ωt) /dt = ωNBA. sen ωt
Una espira tiene área de 0.100 m2 y gira a 60.0 rev/s, con su eje de rotación perpendicular a un campo magnético uniforme de 0.200 T. Sabiendo que la bobina tiene 1000 vueltas encontrar: a) La fem máxima que se genera, b) La orientación de la bobina en relación con el campo magnético cuando ocurre la fem máxima inducida.
Solución
a) La fem máxima es εmax = ωNBA
Antes de proceder a sustituir los valores, hay que pasar la frecuencia de 60 rev/s a unidades del Sistema Internacional. Se sabe que 1 revolución equivale a una vuelta o 2p radianes:
60.0 rev/s = 120p radianes/s
εmax = 120p radianes x 1000 vueltas x 0.200 T x 0.100 m2 = 7539.82 V = 7.5 kV
b) Cuando este valor ocurre sen ωt = 1 por lo tanto:
ωt = θ = 90º,
En tal caso, el plano de la espiral es paralelo a B, de manera que el vector normal a dicho plano forme 90º con el campo. Esto ocurre cuando el vector en color negro en la figura 8 sea perpendicular al vector verde que representa al campo magnético.
- Boylestad, R. 2011. Introducción al análisis de circuitos. 12va. Edición. Pearson. 327-376.
- Figueroa, D. 2005. Electromagnetismo. Serie Física para Ciencias e Ingeniería. Volumen 6. Editado por D. Figueroa. Universidad Simón Bolívar. 115 y 244-245.
- Figueroa, D. 2006. Laboratorio de Física 2. Editorial Equinoccio. 03-1 y 14-1.
- Ondas senoidales. Recobrado de: iessierradeguara.com
- Serway, R. 2008.Física para Ciencias e Ingeniería. Volumen 2. Cengage Learning. 881- 884
