Física
2020-08-04T08:08:42+02:00

Vectores unitarios: características, cómo sacarlo, ejemplos

---

Los vectores unitarios son aquellos cuyo módulo, magnitud o tamaño es igual al valor numérico uno. Los vectores unitarios son de utilidad para indicar la dirección de otros vectores no unitarios.

Recordemos que los vectores son entidades matemáticas que representan matemáticamente las magnitudes físicas que dependen de la dirección, como lo son la fuerza, la velocidad, la aceleración y otras.

Independientemente de la magnitud física a la que se asocien, los vectores unitarios son entes carentes de unidades de medida y su tamaño siempre es 1, un número puro.

Por ejemplo, la velocidad de una partícula que se mueve a 3 m/s y va en la dirección positiva del eje cartesiano X se denota: v = (3 m/s) i, donde la letra negrita se usa para denotar las cantidades vectoriales. En este ejemplo el módulo de v es 3 m/s y el módulo del vector unitario i es 1 (sin unidades).

Índice del artículo

• 1 Módulo, dirección y sentido
• 2 Características de un vector unitario
• 3 Los vectores unitarios en el espacio
• 4 ¿Cómo sacar/calcular el vector unitario?
  • 4.1 Un vector arbitrario en términos del vector unitario
  • 4.2 Representación gráfica
• 5 Ejemplos de vectores unitarios
  • 5.1 Los vectores unitarios perpendiculares i, j y k
  • 5.2 La ley de Coulomb
• 6 Ejercicio resuelto
  • 6.1 Solución
• 7 Referencias

Módulo, dirección y sentido

Dado lo importante que es establecer la orientación que tienen estas magnitudes para conocer sus efectos, los vectores tienen tres características relevantes: la magnitud o módulo, asociado al tamaño del vector, la dirección y el sentido. Al momento de representar una cantidad vectorial es necesario indicar claramente estos aspectos.

Ahora bien, un vector unitario puede tener cualquier dirección y el sentido que se prefiera, pero la magnitud siempre debe ser igual a 1.

Los vectores unitarios se utilizan para señalar una dirección particular en el espacio o en el plano. Si por ejemplo necesitamos trabajar con todas las fuerzas que actúen a lo largo del eje horizontal, pues un vector unitario en esa dirección nos ayuda a distinguir estas fuerzas de otras dirigidas en una dirección diferente.

Y para distinguirlos de los vectores no unitarios, se suele utilizar en letra impresa la negrita y colocar un acento circunflejo encima, por ejemplo:

Características de un vector unitario

Matemáticamente el vector unitario:

Entonces podemos establecer que:

-El módulo del vector unitario siempre es 1, no importa si se trata de un vector fuerza, velocidad u otro.

-Los vectores unitarios tienen una determinada dirección, así como sentido, como por ejemplo el vector unitario en la dirección vertical, que puede tener sentido hacia arriba o bien hacia abajo.

-Los vectores unitarios tienen un punto de origen. Cuando se los representa mediante un sistema de coordenadas cartesianas, dicho punto coincide con el origen del sistema: (0,0) si se trata del plano o (0,0,0) si el vector está en el espacio tridimensional.

-Asimismo con los vectores unitarios se pueden realizar todas las operaciones de suma, resta y multiplicación vectorial que se hacen mediante los vectores regulares. Por lo tanto es válido multiplicar el vector unitario por un escalar, así como llevar a cabo el producto punto y el producto cruz.

-Con un vector unitario en determinada dirección se pueden expresar otros vectores que también estén orientados en dicha dirección.

Los vectores unitarios en el espacio

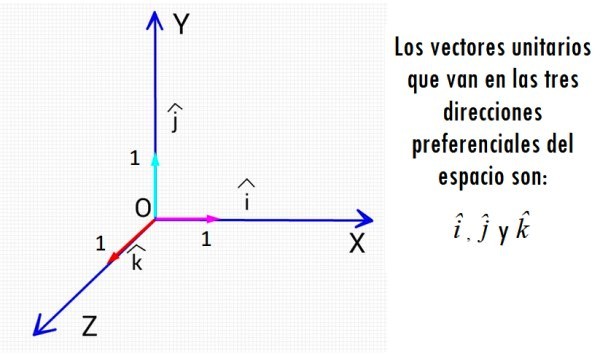
Para expresar un vector cualquiera en el espacio o en el plano, se puede utilizar un conjunto de vectores unitarios perpendiculares entre sí, que forman una base ortonormal. Cada una de las tres direcciones preferenciales del espacio tiene su propio vector unitario.

Volvamos de nuevo al ejemplo de las fuerzas dirigidas a lo largo del eje horizontal. Este es el eje x, que tiene dos posibilidades: sentido hacia la derecha y sentido hacia la izquierda. Supongamos que se tiene un vector unitario sobre el eje x y dirigido hacia la derecha, al cual podemos denotar mediante alguna de estas formas:

Cualquiera de ellas es válida. Ahora bien, supongamos una fuerza F₁ de magnitud 5 N a lo largo de este eje y dirigida hacia la derecha, tal fuerza podría expresarse como:

Si la fuerza estuviera dirigida a lo largo del eje x pero en sentido contrario, es decir, hacia la izquierda, entonces se podría utilizar un signo negativo para establecer esta diferencia.

Por ejemplo, una fuerza de 8 N de magnitud, ubicada sobre el eje x y dirigida hacia la izquierda quedaría así:

O bien así:

Y para los vectores que no están dirigidos a lo largo de los ejes cartesianos, también hay forma de representarlos en términos de los vectores unitarios ortogonales, mediante sus componentes cartesianas.

¿Cómo sacar/calcular el vector unitario?

Para calcular el vector unitario en la dirección de cualquier vector arbitrario v, se aplica la siguiente fórmula:

Donde:

Es el módulo o magnitud del vector v, cuyo cuadrado se calcula así:

|v|² = (v_x)² +  (v_y)²+  (v_z)²

Un vector arbitrario en términos del vector unitario

Alternativamente el vector v se puede expresar así:

Es decir, el producto de su módulo por el vector unitario correspondiente. Esto es exactamente lo que se hizo antes, al hablar de la fuerza de 5 N de magnitud dirigida a lo largo del eje x positivo.

Representación gráfica

Gráficamente lo antes dicho se ve en esta imagen, donde el vector v está en color azul y el vector unitario correspondiente en su dirección está en rojo.

En este ejemplo, el vector v tiene una magnitud mayor que la del vector unitario, pero la explicación es válida aún si no ocurre así. En otras palabras, podemos tener vectores que sean por ejemplo 0.25 veces el vector unitario.

Ejemplos de vectores unitarios

Los vectores unitarios perpendiculares i, j y k

Como hemos visto antes, los vectores unitarios perpendiculares i, j y k son  muy útiles para representar cualquier otro vector en el plano o el espacio, y llevar a cabo las operaciones vectoriales. En términos de dichos vector, un vector arbitrario v se representa como:

v = v_xi + v_yj + v_zk

Donde v_x, v_y y v_z son las componentes rectangulares del vector v, que son escalares –no se usan negritas para representarlas en texto impreso-.

La ley de Coulomb

Los vectores unitarios aparecen frecuentemente en Física. Ahí tenemos a la ley de Coulomb, por ejemplo, que describe cuantitativamente la interacción entre dos cargas eléctricas puntuales.

En ella se señala que la fuerza F de atracción o repulsión entre dichas cargas es proporcional al producto de las mismas, inversamente proporcional al cuadrado de la distancia que las separa y está dirigida en la dirección del vector unitario que une a las cargas.

A este vector se le suele representar mediante:

Y la ley de Coulomb queda así, en forma vectorial:

Ejercicio resuelto

Hallar el vector unitario en la dirección del vector v = 5i + 4j -8k, dado en unidades arbitrarias.

Solución

Se aplica la definición de vector unitario dada anteriormente:

Pero antes hay que calcular el módulo del vector, que como tiene tres componentes, se determina mediante:

|v|² = (v_x)² +  (v_y)² +  (v_z)²

Quedando:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Por lo tanto el módulo de v es:

|v|=√105

El vector unitario buscado es simplemente:

Que nos lleva finalmente a:

 v = 0.488 i + 0.390 j – 0.781 k

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
2. Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
3. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
4. Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
5. Resnick, R. (1999). Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.