Función real de variable real y su representación gráfica

Una función real de variable real toma un número perteneciente al conjunto de los números reales y lo asocia a otro valor, también real, a través de una regla de correspondencia unívoca. Esto quiere decir que el número real obtiene, mediante esta regla, una imagen única.

Las variables numéricas de partida suelen designarse mediante la letra x, mientras que su imagen es la letra y. Por su parte, a la regla de correspondencia que las vincula se la llama también con alguna otra letra del alfabeto, como la “f” de función, aunque puede usarse  otra.  En notación compacta se escribe:

f: x → y = f(x)

A la variable  x se le llama variable independiente, mientras que la y es la variable dependiente. La función puede expresarse de varias maneras, por ejemplo a través de un enunciado matemático como estos:

• f(x) = 2x −3
• h(x) = −3x²

Otra forma de expresión es a través de una gráfica, que es muy útil porque permite apreciar el comportamiento de la función de un solo vistazo. Construir una gráfica es muy sencillo usando un sistema de coordenadas cartesianas, en el que se representan los pares[x, f(x)] como puntos en el plano. Después se unen mediante una línea suave y continua y listo, ya se puede ver cómo es la función.

Ejemplos

Para construir la gráfica se puede recurrir a una tabla de valores en la que se colocan los puntos a graficar. Para la variable x se seleccionan valores que pertenezcan al dominio de la función, es decir, aquellos que al ser sustituidos en la fórmula, arrojan a su vez números reales.

Una vez escogidos los valores de x, se procede a determinar su imagen y=f(x), y de esta manera se obtienen los pares de puntos [x, f(x)] que se van a graficar.

Hay unos puntos que son importantes y deben ser incluidos en la tabla: aquellos en los que la gráfica corta a los ejes coordenados, eso si existen, porque no todas las funciones los intersectan.

Para calcularlos se procede de la siguiente manera:

–Intersección con el eje y: se hace x=0 en la fórmula de la función y se calcula el valor de y correspondiente.

–Intersección con el eje x: se hace y=0 y se resuelve la ecuación f(x)=0.

A continuación se dibuja el sistema de coordenadas cartesianas y se grafican cada uno de los puntos, que se unen luego con una línea suave y continua de ser posible.

Ejemplo 1

Construir una tabla de valores y la gráfica de la siguiente función:

f(x) = x² −4

Antes de comenzar hay que hallar el dominio de la función, que es el conjunto de valores reales para los cuales existe la función. Como se trata de una función cuadrática, cualquier valor de x que pertenezca a los números reales tiene una imagen real, de acuerdo a f(x).

Entonces, la tabla se puede construir eligiendo cualquier valor de x, y lo más sencillo es comenzar con las intersecciones de la gráfica con los ejes, si es que las hay. Después de encontrarlas, entonces se buscan otros puntos para completar la tabla.

Para x = 0

f(0) = −4

Por lo tanto, el primer punto de la tabla es (0, −4). Esta es la intersección de la gráfica con el eje y.

Para y = 0

Seguidamente se  hace y = 0 y se resuelve la ecuación que resulta:

x² −4=0

x² = 4

Las soluciones de esta ecuación son: x₁= 2 y x₂= −2. Por lo tanto hay dos intersecciones con el eje x, que son los puntos: (−2,0) y (2,0).

Ahora se pueden encontrar más puntos que añadir a la tabla de valores:

Para x = 1

f(1) = (1)² − 4 = −3

Para x = − 1

f(−1) = (−1)² − 4 = −3

Para x =  3

f(3) = (3)² − 4 = 5

Para x =  −3

f(−3) = (−3)² − 4 = 5

Tabla de valores

En la siguiente tabla se muestran los puntos obtenidos, los cuales servirán para construir la gráfica de f(x):

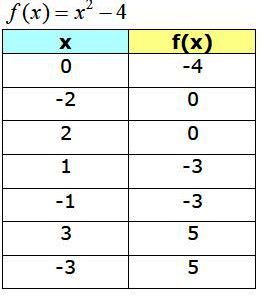
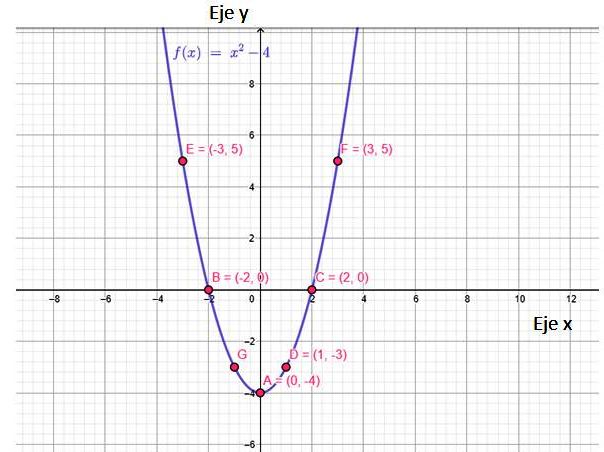
La gráfica de esta función es una parábola, que abre hacia arriba y tiene en A un punto mínimo, llamado vértice, de coordenadas (0,−4). Es interesante destacar que los valores de f(x) comienzan en y = -4 hasta ∞. Este es el rango de la función.

De la gráfica se puede concluir que la función es continua, decreciente en el intervalo (−∞,0) y creciente a partir de allí.

Ejemplo 2

Teniendo la gráfica de la función es posible conocer su dominio, su rango, las intersecciones que tiene con los ejes y visualizar su comportamiento general (crecimiento y decrecimiento).

A continuación se muestra la gráfica de la función polinómica:

f(x) = − x⁴+4x²+1

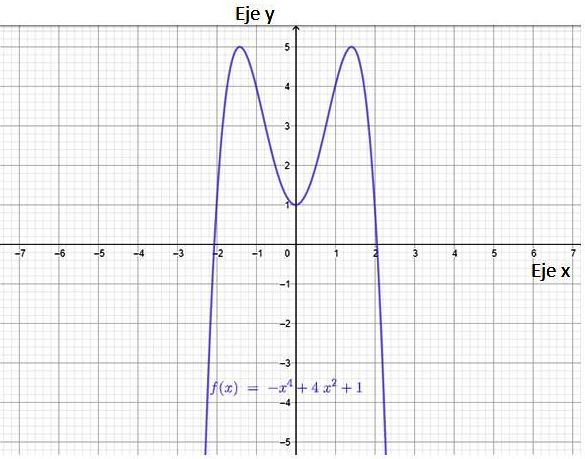
De la imagen se deduce que la función tiene dos intersecciones con el eje x, los puntos (-2,0) y (2,0). También tiene una intersección con el eje y, el punto (0,1).

El dominio de una función polinomial es el conjunto completo de los números reales, también se advierte que la función es continua y tiene simetría alrededor del eje vertical. En efecto, se puede comprobar que esta función es de simetría par. Una función es par si cumple:

f(x) = f(–x)

El lector puede comprobar que al sustituir –x en la función, esta no se altera.

Hay dos puntos interesantes, que están a la altura de y = 5, son los valores máximos de la función. El rango de esta función, es decir, el conjunto de valores que toma la variable y, se extiende desde -∞ hasta y =5 precisamente.

Para saber los valores de x cuya imagen es y =5, se sustituye este valor en la función:

5 = − x⁴+4x²+1

Y se obtiene esta ecuación:

− x⁴ + 4x² − 4 = 0

Cuyas soluciones son −√2 y + √2. Pues bien, la función es:

–Creciente desde x -∞ hasta x = −√2

–Decreciente desde x=  −√2 hasta x=0

–Creciente desde x = 0 hasta x = + √2

–Decreciente desde x = + √2 en adelante.

Ejercicio resuelto

Construir la gráfica de la siguiente función:

f(x)=√(x-5)

Solución

Primero hay que determinar el dominio de la función, para saber qué valores de x  se pueden escoger para construir la tabla. En el caso de la función propuesta, la cantidad dentro de la raíz debe ser siempre positiva o igual a 0, por lo tanto:

x−5 ≥ 0

x ≥ 5

Por lo tanto, para la tabla solamente se pueden escoger valores mayores o iguales a 5. En cuanto a las intersecciones con los ejes coordenados, la única posibilidad es hacer y = 0, y entonces x = 5.

No sirve hacer x = 0 para esta función, pues este valor no pertenece al dominio.

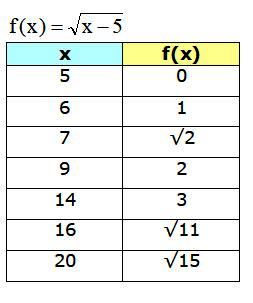
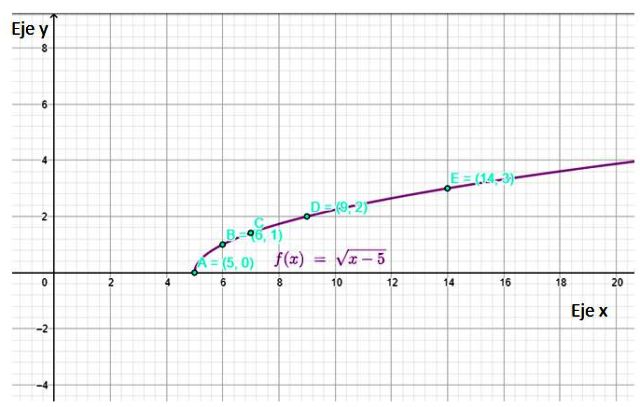
La gráfica obtenida es:

Referencias

1. E-Math Zone. Types of Functions. Recuperado de: emathzone.com.
2. Hoffman, J.G. Selección de Temas de Matemática. Ed. Sphinx.
3. Math is Fun. Commons Functions Reference. Recuperado de: mathisfun.com.
4. Requena, B. Universo Fórmulas. Tipos de Funciones. Recuperado de: universoformulas.com.
5. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.