Interpolación de Lagrange: polinomios, características, ejemplos

¿Qué es la interpolación de Lagrange?

La interpolación de Lagrange es un método numérico de aproximación de funciones, el cual hace uso de un polinomio que pasa por ciertos puntos conocidos de la función que se pretende aproximar.

Si la función a aproximar es suave, aún fuera de los valores dados o conocidos, el polinomio toma valores cercanos a los de la función de interés, sobre todo si dichos valores están comprendidos entre los puntos dados. Por eso el polinomio se considera una buena aproximación a la función.

Ahora bien, supóngase que se desea aproximar una función f(x) de la que solo se conocen sus valores en algunos x­_i­, con i desde 0 hasta n-1. Es decir, se conocen n puntos (x­­­­_i, y_i) con y_i = f(x_i), donde el índice i va desde 0 hasta n-1.

En el método de interpolación de Lagrange, el polinomio que aproxima a la función f(x) es un polinomio P(x) de grado n-1, construido mediante la combinación lineal de n polinomios L_i(x) de grado n-1. Estos son los polinomios de Lagrange, que se expresan de la siguiente manera:

Los valores de y_i representan las ordenadas correspondientes a las abscisas x_i donde la función f(x) es conocida, es decir: y_i = f(x_i).

Polinomios de Lagrange

Mediante combinaciones lineales entre ellos, los polinomios de Lagrange actúan como base para construir el polinomio de grado n -1 que servirá para interpolar los n puntos conocidos.

La notación para los polinomios es L_i(x), con el índice i en el rango desde 0 hasta n-1. La fórmula para establecer los polinomios de Lagrange es la siguiente:

El símbolo mostrado señala que se debe realizar la productoria de n –1 monomios, comenzando desde el polinomio j = 0.

Características de los polinomios de Lagrange

1.- Los polinomios de Lagrange  son exactamente iguales a la unidad cuando se les evalúa en la abscisa correspondiente a su índice, es decir:

L_i(x_i) = 1

2.- Se anulan en las abscisas de los puntos de interpolación con índice diferente al del mismo polinomio:

L_i(x_j) = 0, con i≠j.

3.- Tomando otros valores de abscisas diferentes a los puntos de interpolación, los polinomios de Lagrange adquieren valores comprendidos entre –1 y +1.

4.- Para obtener los polinomios de Lagrange solo se requiere conocer las abscisas de los puntos a interpolar.

Polinomios de Lagrange de segundo grado

Los polinomios de Lagrange de segundo grado son los que se usan más frecuentemente cuando se desea hacer una interpolación a tres puntos.

Supongamos que se conoce la función a interpolar en tres puntos, los cuales son:

(x₀,y₀); (x₁, y₁); (x₂, y₂)

Entonces sus polinomios de Lagrange correspondientes L₀, L₁ y L₂ se consiguen así:

L₀(x) = [(x – x₁) / (x₀ – x₁)] [(x – x₂) / (x₀ – x₂)]

L₁(x) = [(x – x₀) / (x₁ – x₀)] [(x – x₂) / (x₁ – x₂)]

L₂(x) = [(x – x₀) / (x₂ – x₀)] [(x – x₁) / (x₂ – x₁)]

Debe notarse que L₀(x₀)= L₁(x₁)= L₂(x₂)= 1, mientras que L_i(x_j)= 0 siempre que i≠ j.

Polinomio interpolante de Lagrange de segundo grado

Es importante destacar que en el polinomio interpolante de Lagrange, las ordenadas de los puntos de interpolación son factores de los polinomios de Lagrange.

De esta forma, una vez obtenidos los polinomios para determinados valores de las abscisas, los mismos sirven para calcular el polinomio interpolante de diversas funciones, siempre que se conozca la ordenada en las abscisas previamente fijadas.

Para el caso de un polinomio interpolante de segundo grado:

P(x) = f(x₀) L₀(x) + f(x₁) L₁(x) + f(x₂) L₂(x)

Y P(x) se aproxima a la función f(x) en el intervalo (x₀, x₂).

Ejemplos

Ejemplo 1

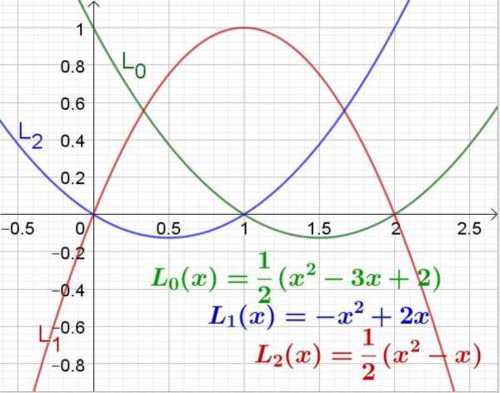
Hallar los polinomios de Lagrange correspondientes a tres puntos de abscisas x₀= 0, x₁= 1 y x₂= 2.

De acuerdo a lo visto en la sección previa, estos polinomios serán:

L₀(x) = [(x – 1) / (0 – 1)] [(x – 2) / (0 – 2)]= -(x –1) ⋅ (-½) (x – 2) = ½(x² – 3x + 2)

L₁(x) = [(x – 0) / (1 – 0)] [(x – 2) / (1 – 2)]= x ⋅ (–1) (x – 2) = – x² + 2x

L₂(x) = [(x – 0) / (2 – 0)] [(x – 1) / (2 – 1)]= (½) x ⋅ (x – 1) = (½)(x² – x)

Ejemplo 2

Se desea aproximar la función f(x)= Arctan(x) en el intervalo [0, 2]. De esta función solo se conocen sus valores para x₀= 0, x₁= 1 y x₂= 2, los cuales son respectivamente y₀= 0, y₁= π/4= 0,785 y y₂= 1,107.

Por lo tanto hay que hallar el polinomio interpolante P(x) que se aproxima a f(x) en el intervalo indicado.

En el ejemplo 1 ya se determinaron los polinomios de Lagrange para los valores de abscisas señalados en este enunciado, por lo que no es preciso repetir el cálculo. El polinomio interpolante ahora será:

P(x) = f(x₀) L₀(x) + f(x₁) L₁(x) + f(x₂) L₂(x)

Lo cual equivale a:

P(x) = y₀ L₀(x) + y₁ L₁(x) + y₂ L₂(x)

En este caso específico resulta:

P(x) = 0∙ (½) (x² – 3x + 2) + 0,785∙ (– x² + 2x) + 1,107∙ (½) (x² – x)

Lo anterior se simplifica a:

P(x) = 0,785 ∙ (- x² + 2x) + 1,107∙ (½) (x² – x)

Y finalmente queda:

P(x) = -0,2315∙x² + 1,0165∙x

Ejercicios

Ejercicio 1

Obtener los polinomios de Lagrange adecuados para tener una aproximación a la función:

f(x)= sen (x)

En el intervalo [0, π] y con cinco puntos de interpolación.

Solución

En primer lugar se determinan las abscisas de los puntos de interpolación, que se escogen equiespaciadas e incluyendo los extremos del intervalo de aproximación. Con esto se tiene:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Como f(x) se anula en los puntos extremos, no será necesario obtener los polinomios de Lagrange L₀ y L₄.

Los polinomios L₁, L₂ y L₃ son:

L₁ = [(x – x₀) / (x₁ – x₀)] [(x – x₂) / (x₁ – x₂)] [(x – x₃) / (x₁ – x₃)] [(x – x₄) / (x₁ – x₄)]

L₂ = [(x – x₀) / (x₂ – x₀)] [(x – x₁) / (x₂ – x₁)] [(x – x₃) / (x₂ – x₃)] [(x – x₄) / (x₂ – x₄)]

L₃ = [(x – x₀) / (x₃ – x₀)] [(x – x₁) / (x₃ – x₁)] [(x – x₂) / (x₃ – x₂)] [(x – x₄) / (x₃ – x₄)]

Ahora sustituimos el valor de las abscisas:

L₁ = [(x – 0) / (π/4 – 0)] [(x – π/2) / (π/4 – π/2)] [(x – 3 π/4) / (π/4 – 3 π/4)] [(x – π) / (π/4 – π)]

L₂ = [(x – 0) / (π/2 – 0)] [(x – π/4) / (π/2 – π/4)] [(x – 3 π/4) / (π/2 – 3 π/4)] [(x – π) / (π/2 – π)]

L₃ = [(x – 0) / (3 π/4 – 0)] [(x – π/4) / (3 π/4 – π/4)] [(x – π/2) / (3 π/4 – π/2)] [(x – π) / (3 π/4 – π)]

Se resuelven los denominadores:

L₁ = [x / π/4] [(x – π/2) / (– π/4)] [(x – 3 π/4) / (-π/2)] [(x – π) / (-3π/4)]

L₂ = [x / π/2] [(x – π/4) / (π/4)] [(x – 3 π/4) / (-π/4)] [(x – π) / (-π/2)]

L₃ = [x / (3 π/4)] [(x – π/4) / (π/2)] [(x – π/2) / (π/4)] [(x – π) / (-π/4)]

Se simplifica y se reagrupa para obtener:

L₁ = x (x – π/2) (x – 3 π/4) (x – π) / (-3 π ⁴/128)

L₂ = x (x – π/4) (x – 3 π/4) (x – π) / (π ⁴/64)

L₃ = x (x – π/4) (x – π/2) (x – π) / (-3 π ⁴/128)

Ejercicio 2

Obtener el polinomio de interpolación que aproxima a la función sen(x) en el intervalo [0, π] con los cinco puntos de interpolación elegidos en el ejercicio 1 y sus respectivos polinomios de Lagrange.

Solución

El polinomio de interpolación es:

P(x) = sen(0) * L₀ + sen(π/4) * L₁ + sen(π/2) * L₂ + sen(3π/4) * L₃ + sen(π) * L4

Evaluando la función seno y multiplicando se tiene:

P(x) = (√2/2)L₁ + 1 * L₂ + (-√2/2)L₃

Después de un arduo trabajo algebraico se tiene que el polinomio interpolante es:

P(x)= 2. 7481 x⁴ –15. 138 x³ +23. 467 x² – 9. 5236 x

Referencias

1. Goodman, A. L. H. 1996. Álgebra y trigonometría con Geometría analítica. Pearson Educación.
2. Harpe, P. d. (2000). Topics in Geometric Group Theory. University of Chicago Press.
3. Hazewinkel, M. (2001). Linear interpolation», Encyclopedia of Mathematics.
4. Hoffmann, E. (2002). A chronology of interpolation: from ancient astronomy to modern signal and image processing. Proceedings of the IEEE.
5. Wikipedia. Interpolación polinómica de Lagrange. Recuperado de: Wikipedia.com