Límites trigonométricos: cómo resolverlos, ejercicios resueltos
Los límites trigonométricos son límites de funciones tales que dichas funciones están formadas por funciones trigonométricas.
Hay dos definiciones que deben ser conocidas para poder entender cómo se realiza el cálculo de un límite trigonométrico. Estas definiciones son:
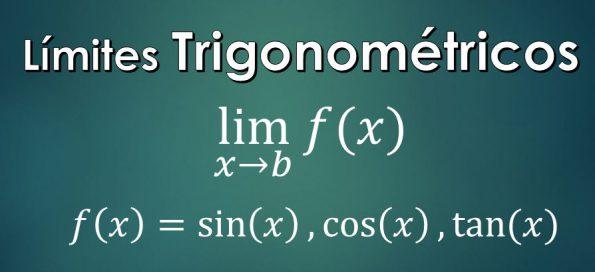
– Límite de una función “f” cuando “x” tiende a “b”: consiste en calcular el valor al cual se aproxima f(x) a medida que “x” se aproxima a “b”, sin llegar a valer “b”.
– Funciones trigonométricas: las funciones trigonométricas son las funciones seno, coseno y tangente, denotadas por sin(x), cos(x) y tan(x) respectivamente.
Las demás funciones trigonométricas se obtienen a partir de las tres funciones mencionadas anteriormente.
Límites de funciones
Para aclarar el concepto de límite de una función se procederá a mostrar algunos ejemplos con funciones sencillas.
– El límite de f(x)=3 cuando “x” tiende a “8” es igual a “3”, puesto que la función siempre es constante. No importa cuánto valga “x”, el valor de f(x) siempre será “3”.
– El límite de f(x)=x-2 cuando “x” tiende a “6” es “4”. Ya que cuando “x” se aproxima a “6” entonces “x-2” se aproxima a “6-2=4”.
– El límite de g(x)=x² cuando “x” tiende a “3” es igual a 9, puesto que cuando “x” se va acercando a “3” entonces “x²” se va acercando a “3²=9”.
Como se puede notar en los ejemplos anteriores, calcular un límite consiste en evaluar el valor al cual tiende “x” en la función, y el resultado será el valor del límite, aunque esto es cierto solo para funciones continuas.
¿Existen límites más complicados?
La respuesta es si. Los ejemplos anteriores son los ejemplos más sencillos de límites. En los libros de cálculo, los principales ejercicios de límites son los que generan una indeterminación del tipo 0/0, ∞/∞, ∞-∞, 0*∞, (1)^∞, (0)^0 y (∞)^0.
Estas expresiones son llamadas indeterminaciones puesto que son expresiones que matemáticamente no tienen sentido.
Además de que, dependiendo de las funciones involucradas en el límite original, el resultado obtenido al resolver las indeterminaciones puede ser diferente en cada caso.
Ejemplos de límites trigonométricos sencillos
Para resolver límites, siempre es muy útil conocer las gráficas de las funciones involucradas. A continuación se muestran las gráficas de las funciones seno, coseno y tangente.
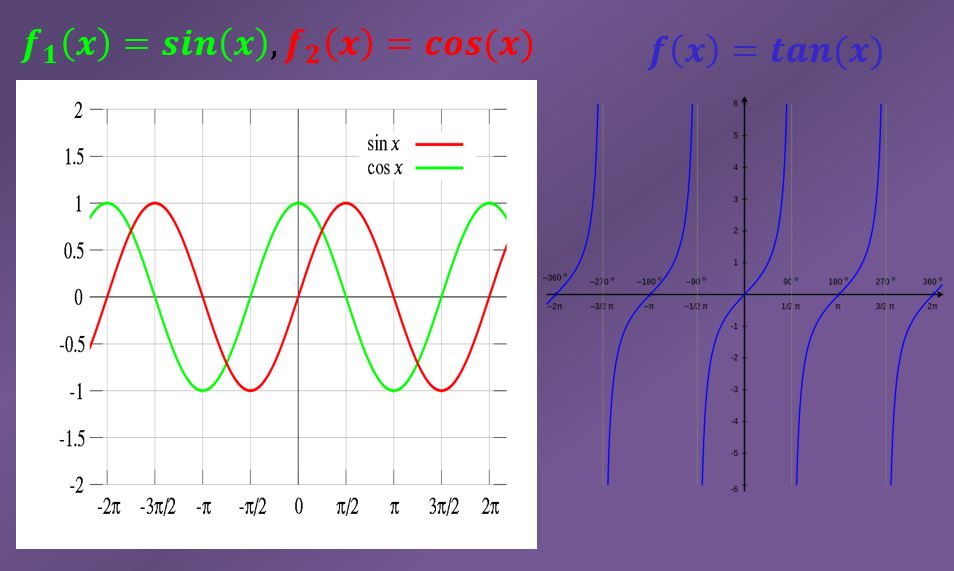
Algunos ejemplos de límites trigonométricos sencillos son:
– Calcule el límite de sin(x) cuando “x” tiende a “0”.
Al ver la gráfica se puede apreciar que si “x” se va acercando a “0” (tanto por la izquierda como por la derecha), entonces la gráfica del seno se va acercando también a “0”. Por lo tanto, el límite de sin(x) cuando “x” tiende a “0” es “0”.
– Calcule el límite de cos(x) cuando “x” tiende a “0”.
Observando la gráfica del coseno se aprecia que cuando “x” está cerca de “0” entonces la la gráfica del coseno está cerca de “1”. Esto implica que el límite de cos(x) cuando “x” tiende a “0” es igual a “1”.
Un límite puede existir (ser un número), como sucede en los ejemplos anteriores, pero también puede ocurrir que no exista como se muestra en el siguiente ejemplo.
– El límite de tan(x) cuando “x” tiende a “Π/2” por la izquierda es igual a “+∞”, como se puede ver en la gráfica. Por otro lado, el límite de tan(x) cuando “x” tiende a “-Π/2” por la derecha es igual a “-∞”.
Identidades de límites trigonométricos
Dos identidades muy útiles cuando se están calculando límites trigonométricos son:
– El límite de “sin(x)/x” cuando “x” tiende a “0” es igual a “1”.
– El límite de “(1-cos(x))/x” cuando “x” tiende a “0” es igual a “0”.
Estas identidades se utilizan muy a menudo cuando se tiene algún tipo de indeterminación.
Ejercicios resueltos
Resuelva los siguientes límites utilizando las identidades descritas arriba.
– Ejercicio 1
Calcule el límite de “f(x)= sin(3x)/x” cuando “x” tiende a “0”.
Si se evalúa la función “f” en “0” se obtendrá una indeterminación del tipo 0/0. Por lo tanto, hay que intentar resolver esta indeterminación utilizando las identidades descritas.
La única diferencia entre este límite y la identidad es el número 3 que aparece dentro de la función seno. Para poder aplicar la identidad se debe reescribir la función “f(x)” de la siguiente manera “3*(sin(3x)/3x)”. Ahora, tanto el argumento del seno como el denominador son iguales.
De modo que cuando “x” tiende a “0”, utilizando la identidad resulta “3*1=3”. Por lo tanto, el límite de f(x) cuando “x” tiende a “0” es igual a “3”.
– Ejercicio 2
Calcule el límite de “g(x)=1/x – cos(x)/x” cuando “x” tiende a “0”.
Cuando se sustituye “x=0” en g(x) se obtiene una indeterminación del tipo ∞-∞. Para resolverla primero se restan las fracciones, lo cual arroja como resultado “(1-cos(x))/x”.
Ahora, al aplicar la segunda identidad trigonométrica se tiene que el límite de g(x) cuando “x” tiende a “0” es igual a 0.
– Ejercicio 3
Calcule el límite de “h(x)=4tan(5x)/5x” cuando “x” tiende a “0”.
Nuevamente si se evalúa h(x) en “0” se obtendrá una indeterminación del tipo 0/0.
Reescribiendo tan(5x) como sin(5x)/cos(5x) resulta que h(x)=(sin(5x)/5x)*(4/cos(x)).
Utilizando que el límite de 4/cos(x) cuando “x” tiende a “0” es igual a “4/1=4” y la primera identidad trigonométrica se obtiene que el límite de h(x) cuando “x” tiende a “0” es igual a “1*4=4”.
Observación
Los límites trigonométricos no son siempre fáciles de resolver. En este artículo solo se mostraron ejemplos básicos.
Referencias
- Fleming, W., & Varberg, D. E. (1989). Precalculus Mathematics. Prentice Hall PTR.
- Fleming, W., & Varberg, D. E. (1989). Precalculus mathematics: a problem-solving approach (2, Illustrated ed.). Michigan: Prentice Hall.
- Fleming, W., & Varberg, D. (1991). Algebra y trigonometría con geometría analítica. Pearson Educación.
- Larson, R. (2010). Precalculus (8 ed.). Cengage Learning.
- Leal, J. M., & Viloria, N. G. (2005). Geometría Analítica Plana. Mérida – Venezuela: Editorial Venezolana C. A.
- Pérez, C. D. (2006). Precalculo. Pearson Educación.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo (Novena ed.). Prentice Hall.
- Saenz, J. (2005). Cálculo Diferencial con funciones trascendentes tempranas para Ciencias e Ingeniería (Segunda Edición ed.). Hipotenusa.
- Scott, C. A. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (reprint ed.). Lightning Source.
- Sullivan, M. (1997). Precalculo. Pearson Educación.
