Tridecágono: propiedades, cómo se hace, ejemplos

¿Qué es un tridecágono?
El tridecágono es una figura geométrica plana de la familia de los polígonos y que se caracterizan por tener 13 lados y 13 vértices. Otro nombre para este polígono es triskaidecágono, vocablo derivado del griego.
Los 13 lados son segmentos de recta que finalmente se cierran para dar forma a la figura. Los polígonos, que se nombran de acuerdo a la cantidad de lados, son una rica fuente de inspiración para la arquitectura, la construcción y el diseño de numerosos objetos, tanto de arte como utilitarios.
Propiedades del tridecágono
El tridecágono comparte con los demás polígonos las siguientes características y propiedades:
–Lados, son los segmentos de recta que se unen para formar la figura, que en el caso del tridecágono son 13. Se los identifica mediante letras minúsculas.
–Vértices, así se llaman los puntos de intersección de los lados consecutivos y suelen denotarse con letras mayúsculas. El tridecágono tiene 13 vértices.
–Perímetro, equivalente a la suma de los lados. Si todos los lados tienen igual medida “a”, el perímetro es simplemente 13×a, pero si los lados son desiguales, entonces el perímetro se encuentra sumando cada una de las longitudes de los lados.
–Centro, es el punto que guarda la misma distancia tanto con los vértices como con los lados.
–Diagonal, una línea que une un vértice a otro vértice no consecutivo (los vértices consecutivos están unidos por los lados).
–Ángulos internos, se forman entre dos lados adyacentes de la figura y por la parte interna del polígono, y su vértice es el vértice común a los dos lados.
–Ángulos externos, se encuentran por fuera del polígono, entre un lado y la prolongación de uno de los lados consecutivos al primero.
–Radio, distancia centro-vértice del tridecágono.
–Ángulo central, es aquel cuyo vértice es el centro del polígono.
–Apotema, segmento que une el centro de un lado con el centro de la figura y forma 90º con dicho lado.
Tridecágonos regulares e irregulares
Los tridecágonos pueden ser:
–Regulares, cuando la medida de todos sus trece lados es la misma y sus ángulos internos miden igual.
–Irregulares, si uno o más de los lados tienen medidas diferentes.
En el caso del tridecágono regular se pueden aplicar las siguientes fórmulas:
Ángulo interno
Para un polígono regular, la fórmula que permite calcular el valor del ángulo interno es:
Donde n representa el número de lados, que en este caso es 13. Con este valor resulta:
I = (11 × 180º)/13 ≈ 152.3º
Diagonales
El número de diagonales se calcula mediante la siguiente fórmula, válida aún si el polígono es irregular:
Para n = 13 resulta:
D = 13× 10/2 = 65 diagonales
Apotema
El valor de la apotema LA se calcula con la siguiente fórmula, siendo “a” la longitud del lado:
LA ≅ 2.0286a
Área
Si se conocen el perímetro P y la longitud de la apotema LA, el área del tridecágono se calcula mediante:
A = (P× LA)/2
En función del lado “a”, la fórmula queda:
A = (13a × LA)/2
Sustituyendo la medida de LA del apartado anterior, se obtiene una fórmula para el área que solo depende de la longitud del lado:
A = (13a × 2.0286a)/2 ≈ 13.186a2
Ejercicio
Si el diámetro de una moneda checa de 20 coronas es 26 mm, ¿Cuánto valen el lado y el área del tridecágono inscrito en la circunferencia de la moneda?
Solución
De la figura se observa un triángulo rectángulo, cuyos catetos son la apotema y la mitad de la longitud del lado, con la hipotenusa igual al radio de la moneda, que es la mitad del diámetro. Como este vale 26 mm, el radio R es igual a 13 mm.
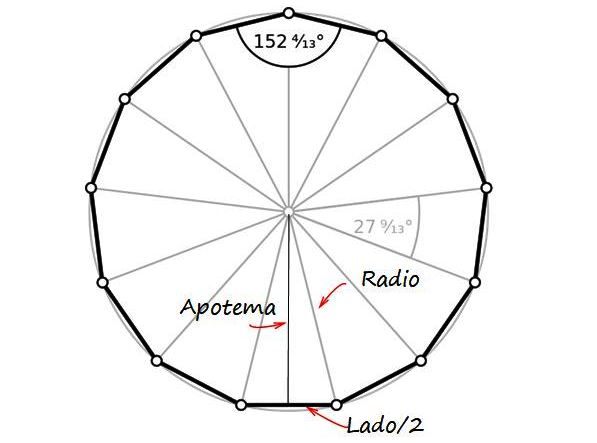
Por teorema de Pitágoras:
Dado que LA ≈ 2.0286a, se tiene:
R2 = (2.0286a)2 + (0.5a)2 = 4.3652a2
El lado es:
Con este valor, el área de la moneda es:
A ≈ 13.186a2 = 13.186(6.222mm)2 = 510.5 mm2
Se deja como ejercicio al lector comparar este resultado con el área obtenida al suponer que la moneda es circular de radio R = 13 mm.
¿Cómo se hace un tridecágono?
El tridecágono regular es de los polígonos que no admite construcción exacta usando solamente regla y compás, es decir, no es un polígono construible. Únicamente son construibles, al menos en teoría, aquellos polígonos cuyo número de lados incluya solo factores primos de la forma:
Los números primos de esa forma se llaman primos de Fermat, pero el número 13, aunque es primo, no tiene esta forma.
Sin embargo, se puede dibujar un tridecágono regular que quede inscrito en una circunferencia, cada vértice tiene intersección con esta, sin que se note imprecisión alguna a simple vista. Para ello es necesario dividir la circunferencia en 13 partes iguales y luego conectar cada vértice con un segmento de recta, correspondientes a cada lado del tridecágono.
Una forma de construir un tridecágono regular, aunque no la única, es dibujando los trazos tal como se muestra en la siguiente animación:
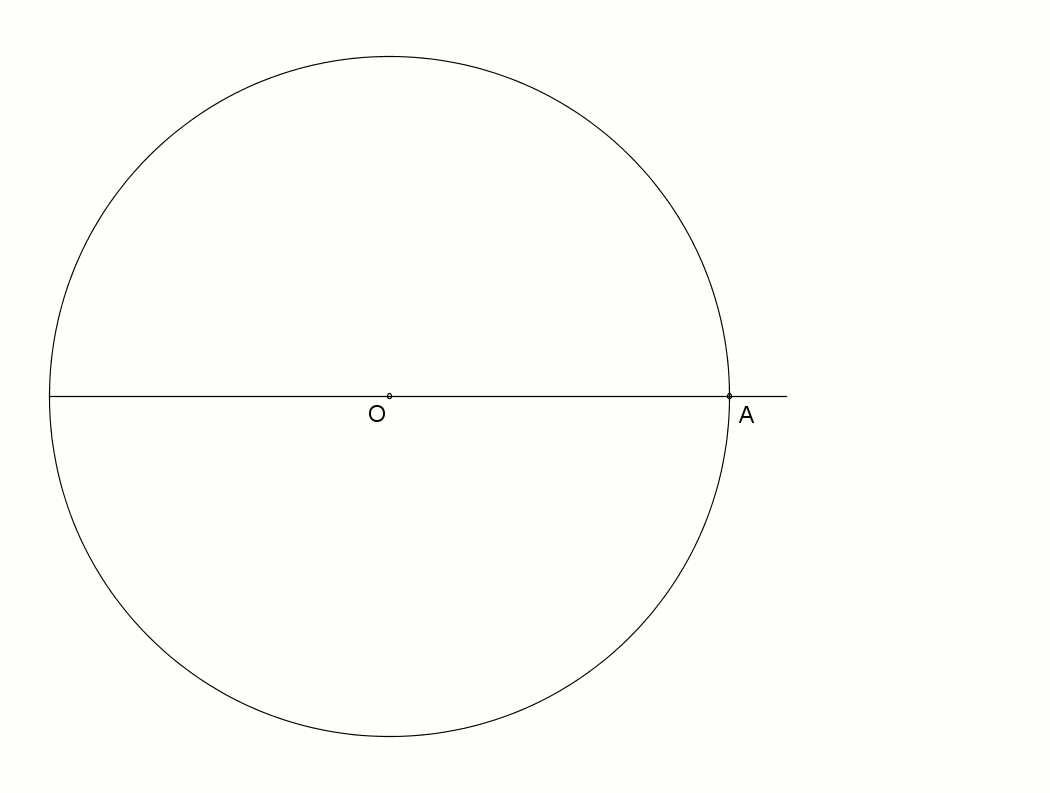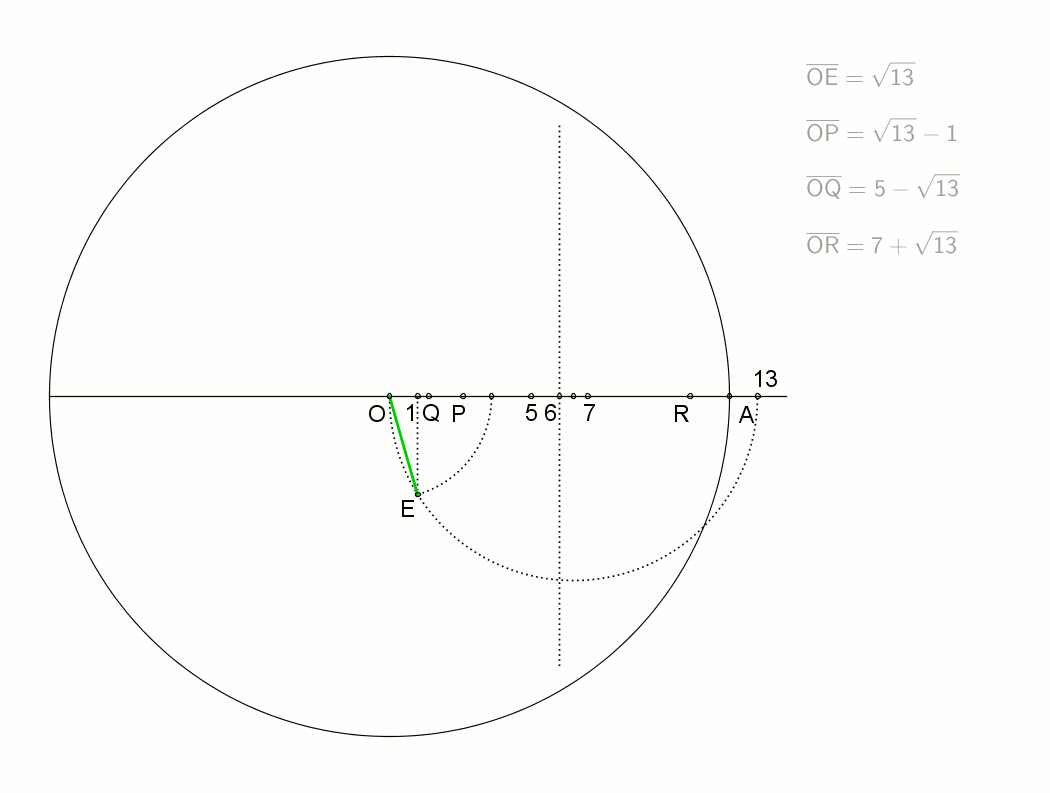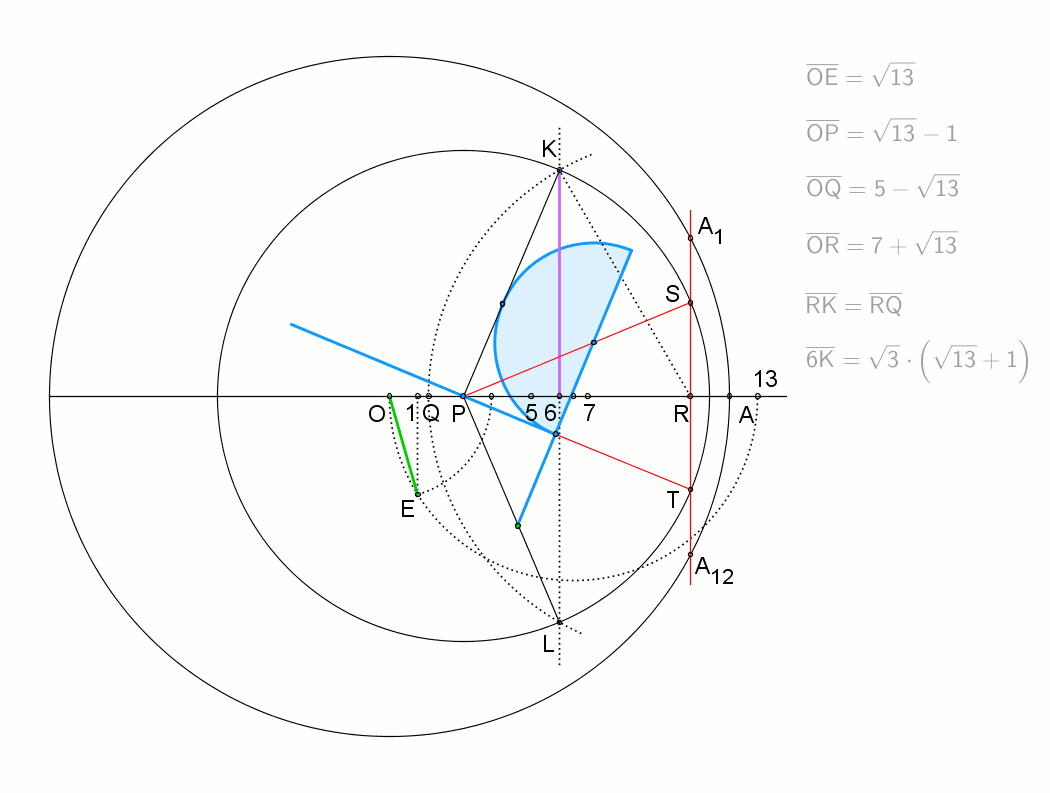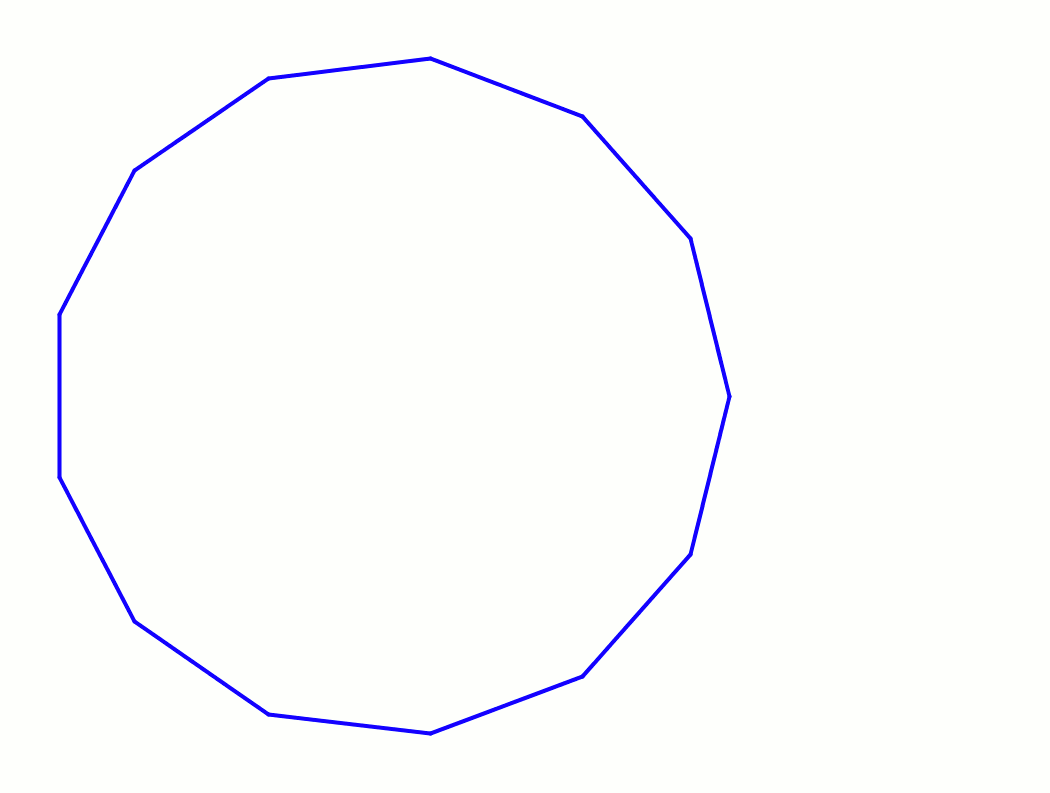
Y esta otra animación también describe cómo hacer un tridecágono de forma aproximada, con regla y compás:

Ejemplos de tridecágonos
Tridecágonos cóncavos y convexos
Cuando los ángulos internos del tridecágono son menores a 180º la figura es convexa, mientras que si uno o más ángulos internos son mayores a 180º, entonces el tridecágono es cóncavo.
El tridecágono regular es convexo, pues sus ángulos internos miden aproximadamente 152.3º cada uno.
Uso del tridecágono en numismática

La numismática es la ciencia de las monedas, las medallas, los billetes y las fichas. Los polígonos de muchos lados son ideales como elementos decorativos en el diseño de monedas, sobre todo los que tienen muchos lados, como el tridecágono.
No todas las monedas son redondas, sin embargo los polígonos de muchos lados se asemejan a la forma circular, cuantos más lados tenga, mayor es la aproximación. Por ello los diseñadores de las monedas hacen uso de los polígonos de muchos lados para introducir un toque de originalidad en su diseño.
Diversos polígonos se usan con este propósito, como la moneda superior, llamada corona y proveniente de la República Checa, un buen ejemplo del uso del tridecágono como elemento de diseño.
Referencias
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- DibujoTecni. Polígonos regulares. Recuperado de: dibujotecni.com.
- Hartley, M. Constructing a tridecagon (triskaidecagon) in a circumcircle with ruler and compass. Recuperado de: youtube.com
- Wikipedia. Polígono construible. Recuperado de: es.wikipedia.org.
- Wikiwand. Tridecagon. Recuperado de: wikiwand.com.
