Heptágono: qué es, regular e irregular, área, fórmula, cómo hacerlo

¿Qué es un heptágono?

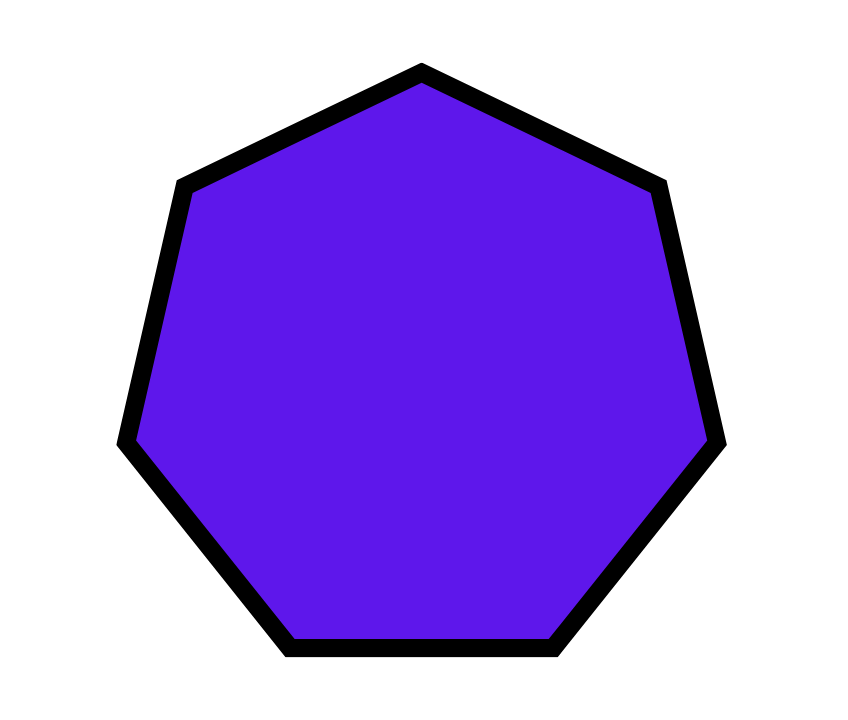
El heptágono es un polígono con siete lados y siete ángulos internos. Como vocablo geométrico, la palabra heptágono se origina del griego hepta, que significa siete, y gonos, que se traduce como ángulo. Es, pues, un polígono con siete ángulos.

Un polígono es una figura geométrica plana que se forma uniendo y cerrando tres o más segmentos, llamados también lados. Los puntos en común que tienen los lados se denominan vértices.

La región entre lados adyacentes, por la parte interior de la figura, es el ángulo interno, cuyo vértice es también uno de los vértices del heptágono.

Si todos los lados y los ángulos internos tienen la misma medida, se trata de un heptágono regular, de lo contrario es un heptágono irregular. Los heptágonos irregulares adoptan gran variedad de formas.

Un heptágono también puede ser convexo o cóncavo, según la medida de sus ángulos internos. Si los ángulos internos miden menos de 180°, el heptágono es convexo, pero si uno o más de dichos ángulos supera los 180°, entonces es cóncavo.

Un heptágono cuyos lados tienen todos igual medida se llama equilateral. Este puede ser cóncavo o convexo, regular o irregular.

Heptágono regular e irregular

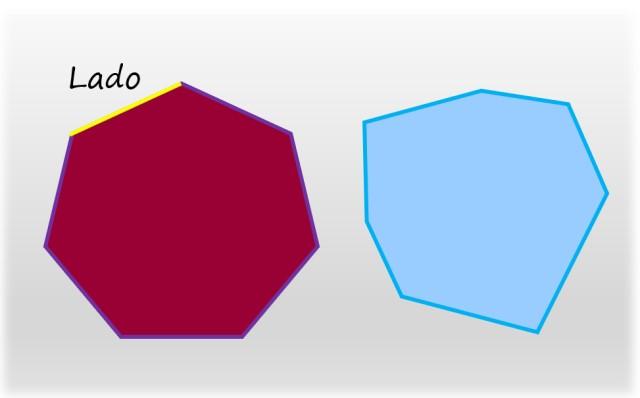
El heptágono regular es aquel que tiene sus siete lados y sus siete ángulos internos de igual medida, lo contrario de un heptágono irregular, que tiene al menos un lado de diferente medida, o bien un ángulo interno distinto.

El heptágono regular

Simetría

Un heptágono regular es una figura altamente simétrica. Se pueden trazar segmentos que conecten un vértice con el punto medio del lado opuesto, todos los cuales se intersectan en el centro del heptágono. Estos son los siete ejes de simetría de la figura.

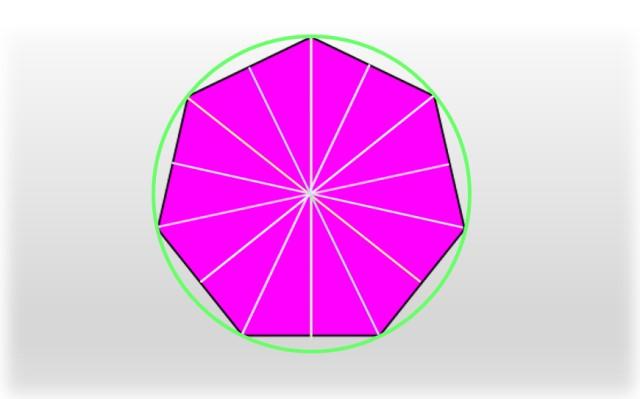
Al segmento que une un vértice con el centro del heptágono se le llama circunradio, pues corresponde al radio de la circunferencia única que pasa por todos y cada uno de los vértices, como se muestra en la figura.

Ángulos

En el heptágono destacan los siguientes ángulos:

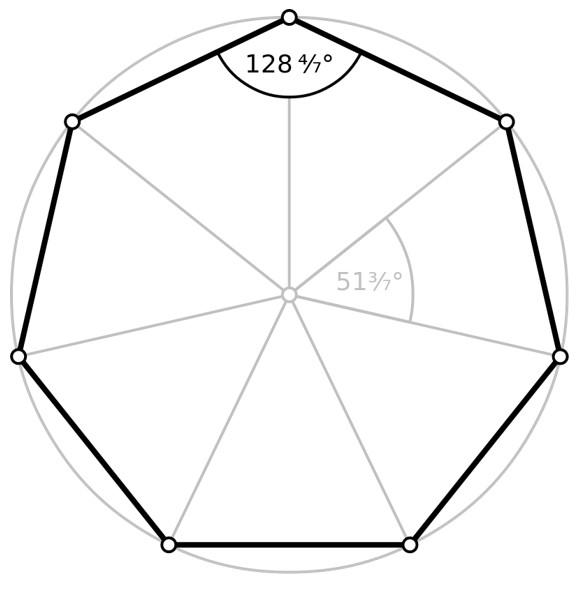
• Ángulo interno ϕ, cuyo vértice coincide con uno de los vértices del heptágono, siendo los lados del ángulo, dos de los lados adyacentes del heptágono. Para un heptágono regular, la medida de cada uno de los siete ángulos internos es aproximadamente 128.57°.
• Ángulo externo, el que se forma entre uno de los lados y la prolongación de uno de los lados adyacentes, siendo el vértice común entre estos dos lados el vértice del ángulo. Igualmente se forman siete ángulos externos y su valor se calcula restando 180° del ángulo interno, que para el heptágono regular, resulta en 51.43°.
• Ángulo central θ, tiene su vértice en el centro del heptágono regular, y sus lados son los radios del heptágono, es decir, los segmentos que conectan el centro con cada vértice, tal como se muestra en la siguiente figura. Se calcula dividiendo 360° entre 7, lo cual da como resultado aproximado 51.43°.

La suma del ángulo interno y el ángulo central es igual a 180°, es decir:

ϕ + θ = π

Área

Para el heptágono regular existen fórmulas, mientras que para el heptágono irregular hay que recurrir a otros métodos, como dividirlo en otros polígonos más sencillos, tales como triángulos.

Área del heptágono regular

1. Si se conocen el perímetro P y la apotema a_p:

Sea A el área del heptágono. Existe una fórmula para calcular el área, válida para cualquier polígono regular:

2. Si se conocen el lado L y la apotema a_p:

Puesto que el perímetro es la suma de los lados, y el lado mide L en el heptágono regular, se obtiene:

P = 7⋅L

Sustituyendo en la fórmula anterior:

3. Si se conoce el lado L        

La siguiente es una fórmula aproximada, válida cuando se conoce la medida del lado L del heptágono:

A = 3.634∙L²

Área del heptágono irregular

El área del heptágono irregular se puede calcular mediante triangulación, que consiste en dividir el heptágono en cinco triángulos (ver la siguiente figura). Se calcula el área de cada uno y se suman los resultados, obteniendo así el área completa del heptágono.

El otro método se denomina determinante de Gauss, y se requiere colocar el heptágono en un sistema de coordenadas rectangulares, con la finalidad de conocer las coordenadas de cada vértice. El área se calcula mediante una fórmula que involucra los valores de dichas coordenadas.

Diagonales

Las diagonales son segmentos que conectan un vértice con otro que no sea consecutivo (si el segmento conecta dos vértices consecutivos es el lado). Un heptágono tiene 14 diagonales en total.

El número de diagonales D de un polígono cualquiera de n lados, se calcula a través de la fórmula:

D = n · (n – 3) / 2

Sustituyendo n = 7, queda:

D = 7 · (7 – 3) / 2 = 7 · (4 / 2) = 14

Suma de los ángulos internos

Para un heptágono cualquiera, sin importar si es regular o no, la suma de sus ángulos internos es igual a 900° o 5π radianes.

Esta propiedad es muy fácil de demostrar, para ello se divide el heptágono en triángulos individuales que no se superpongan, dibujando segmentos rectilíneos que unan los vértices, sin que se crucen unos con otros.

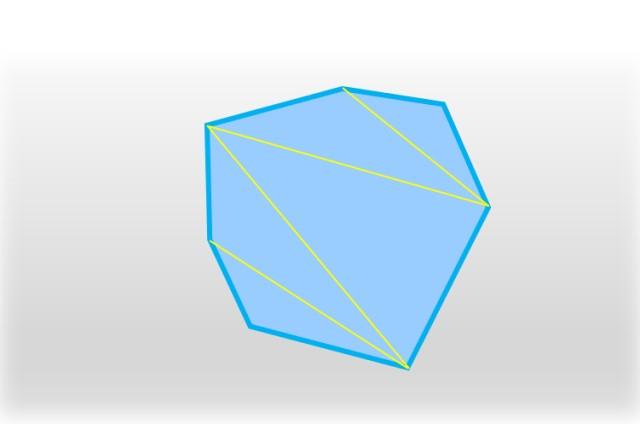
Se obtienen cinco triángulos y en cada uno, la suma de sus ángulos internos es 180°, que multiplicado por 5 es igual a 900°:

5 x 180° = 900°

Fórmulas

Perímetro

Para un heptágono regular de lado L, el perímetro P se calcula así:

P = 7⋅L

Si el perímetro es irregular, se suman las longitudes de cada uno de los siete lados.

Medida del ángulo interno

En un heptágono regular, el ángulo interno θ mide:

θ = [180 (n-2)]/n

Donde n = 7.

Apotema

Sea L el lado del heptágono regular. La apotema es el segmento que va desde el centro del heptágono, perpendicularmente hasta el lado opuesto.

Sea a_p la longitud de la apotema. Conociendo el radio de la circunferencia circunscrita, al que se denota como r_c y el lado L del heptágono, se tiene:

Conociendo el ángulo interno θ, lo anterior equivale a:

Área

Si se trata de un heptágono regular de lado L, el área A viene dada por:

A = 3.634∙L²

Cuando el heptágono es irregular, se necesitan las coordenadas rectangulares de cada vértice, dadas por (x_n , y_n), donde n = 1, 2, 3… 7.

Luego se aplica la siguiente fórmula para encontrar el área A:

Diagonales

El número D de diagonales viene dado por:

D = n · (n – 3) / 2

Donde n = 7 para el heptágono.

Cómo hacer un heptágono

En la siguiente animación se muestra cómo dibujar aproximadamente un heptágono regular, empleando regla y compás.

Referencias

1. Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
2. Lemonis, M. Regular heptagon calculator. Recuperado de: calcresource.com.
3. Math Open Reference. Area of a polygon. Recuperado de: mathopenref.com.
4. Universo Fórmulas. Heptágono. Recuperado de: universoformulas.com.
5. Wikipedia. Heptágono. Recuperado de: es.wikipedia.com.