12 Características de las Ondas (con Ejemplos)
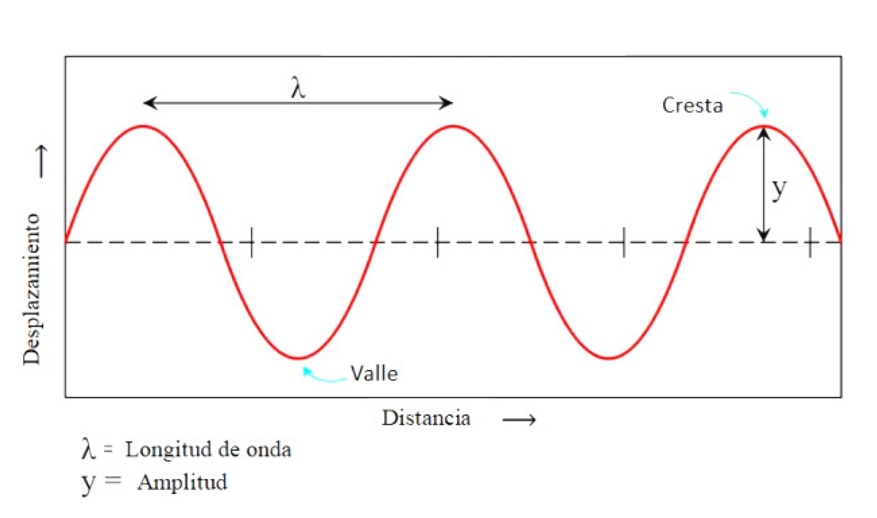
Las características de las ondas son las distintivas del fenómeno ondulatorio: la longitud de onda, la frecuencia, los valles, las crestas, la velocidad, la energía y otras que te explicaremos en este artículo.
En las ondas, no son partículas las que viajan con la perturbación, sino la energía. Cuando una onda se propaga en un medio material, que puede ser agua, aire o una cuerda, entre otros, las partículas apenas se desplazan de la posición de equilibrio, para regresar a ella al cabo de poco tiempo.
Sin embargo, el movimiento se va transmitiendo de una a otra partícula, haciendo que cada una de ellas vibre. De esta manera se va propagando en el medio la perturbación a la que llamamos onda, igual que lo hace la ola de fanáticos en los estadios, cuando se juegan los partidos de fútbol.
El estudio de las ondas es muy interesante, puesto que vivimos en un mundo lleno de ellas: la luz, las olas del mar, el sonido de la música y la voz son todos fenómenos ondulatorios, aunque de diferente naturaleza. Tanto la luz como el sonido son particularmente importantes, pues los necesitamos continuamente para comunicarnos con el mundo exterior.
¿Cuáles son las características de las ondas?
Vibración
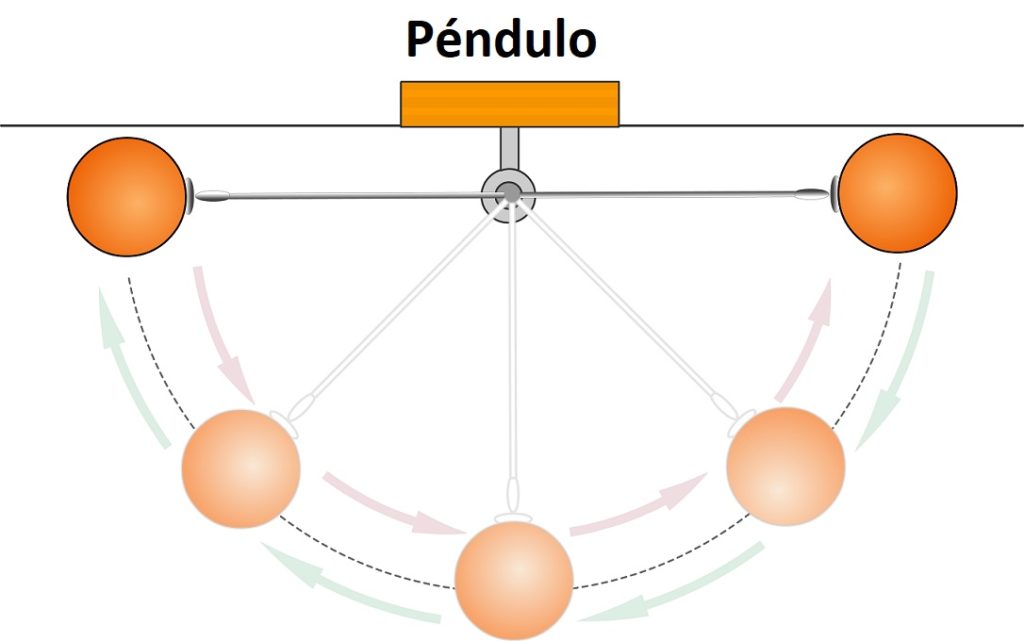
Es el recorrido completo que hace una partícula en su movimiento de vaivén. Por ejemplo un péndulo tiene movimiento de vaivén, puesto que al partir de un punto determinado, describe un arco, se detiene al alcanzar cierta altura y se regresa a su posición original.
Si no fuese por el rozamiento, este movimiento seguiría indefinidamente. Pero a causa de la fricción, el movimiento se hace cada vez más lento y la oscilación menos amplia, hasta que el péndulo se detiene.
Cuando se perturba una cuerda tensa horizontal, las partículas de la cuerda vibran en dirección vertical, esto es, de arriba hacia abajo, mientras que la perturbación viaja horizontalmente a lo largo de la cuerda.
Centro de oscilación
Cuando una partícula hace su movimiento de vaivén, lo hace desplazándose respecto a cierto punto, llamado origen o centro de oscilación.
En el ejemplo del péndulo, este se encuentra en equilibrio en el punto más bajo, y oscila alrededor de este si lo separamos un poco de esta posición. Por lo tanto, este punto se puede considerar el centro de la oscilación.
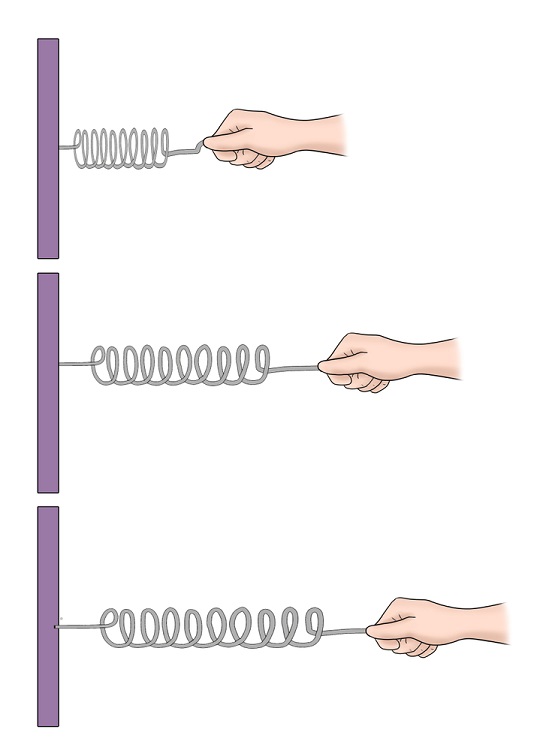
También podemos imaginar un muelle o resorte sobre una mesa horizontal, sujeto por un extremo a una pared, y con un bloque en el otro extremo. Si el sistema muelle-bloque está sin perturbar, el bloque se encuentra en cierta posición de equilibrio.
Sin embargo, al comprimir o estirar un poco al muelle, el sistema comienza a oscilar alrededor de esa posición de equilibrio.
Elongación
Es la distancia que la partícula se aleja del centro de oscilación al cabo de un tiempo. Se mide en metros cuando se emplea el Sistema Internacional SI.
Si se comprime o estira un muelle con un bloque en un extremo, se dice que ha experimentado una elongación de “x” cantidad de metros, centímetros o la unidad que se esté usando para medir distancia.
Crestas y valles
Son, respectivamente, los puntos más altos y los más bajos que alcanza la partícula con respecto a la posición de equilibrio y=0 (ver figura 1).
Amplitud

Es la distancia máxima que la partícula se separa del centro de oscilación y también viene dada en metros. Se denota como A o como y. Allí la posición de equilibrio coincide con y = 0 y corresponde a las crestas y los valles de la onda.
La amplitud es un parámetro importante, pues está relacionado con la energía que transporta la onda. Cuanto mayor sea la amplitud, mayor la energía, como sucede con las olas del mar, por ejemplo.
Nodo
Los nodos son los puntos en los cuales la partícula pasa por el centro de oscilación o posición de equilibrio.
Ciclo
Se llama así a una oscilación completa, cuando la partícula pasa de una cresta a la siguiente, o de un valle al próximo. Entonces decimos que realizó un ciclo.
El péndulo ejecuta una oscilación completa cuando se le aleja una cierta altura de la posición de equilibrio, pasa por el punto más bajo, sube a la misma altura en viaje de ida y regresa a la altura inicial en viaje de vuelta.
Período
Dado que las ondas son repetitivas, el movimiento de las partículas es periódico. El período es el tiempo que se tarda en realizar una oscilación completa y suele denotarse con la letra T mayúscula. Las unidades del período en el Sistema Internacional SI son los segundos (s).
Frecuencia
Es la magnitud inversa o recíproca del período y está relacionada con la cantidad de oscilaciones o ciclos realizados por unidad de tiempo. Se la denota mediante la letra f.
Como la cantidad de oscilaciones no es una unidad, para la frecuencia se emplean los segundos-1 (s-1), denominados Hertz o hertzios y abreviados Hz.
Al ser la inversa del período, podemos escribir una relación matemática entre ambas magnitudes:
f = 1 /T
O bien:
T = 1/f
Si por ejemplo un péndulo ejecuta 30 ciclos en 6 segundos, su frecuencia es de:
f = (30 ciclos)/(6 s) = 5 ciclos/s = 5 Hz.
Longitud de onda
Es la distancia entre dos puntos de una onda que se encuentran a la misma altura, siempre que se haya realizado una oscilación completa. Se puede medir desde una cresta hasta otra consecutiva, por ejemplo, pero también de valle a valle.
La longitud de onda se denota mediante la letra griega λ, que se lee “lambda” y se mide en unidades de distancia como los metros del Sistema Internacional, aunque existe una variedad tan grande de longitudes de onda, que los múltiplos y submúltiplos son frecuentes.
Número de onda
Es la magnitud inversa de la longitud de onda, multiplicada por el número 2π. Por lo tanto, al denotar al número de onda mediante la letra k, tenemos:
k = 2π / λ
Velocidad de propagación
Es la velocidad con la que viaja la perturbación. Si el medio en el cual se propaga la onda es homogéneo e isótropo, es decir, sus propiedades son las mismas en todas partes, entonces esta velocidad es constante y viene dada por:
v = λ / T
Las unidades de la velocidad de propagación son las mismas que las de cualquier otra velocidad. En el Sistema Internacional corresponde a m/s.
Como el período es el inverso de la frecuencia, también se puede expresar:
v = λ . f
Y como la velocidad es constante, el producto λ.f también, de manera que si por ejemplo se modifica la longitud de onda, la frecuencia cambia para que el producto siga siendo el mismo.
Referencias
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
