Ecuaciones polinómicas: qué son, tipos, ejemplos, ejercicios

¿Qué son las ecuaciones polinómicas?

Las ecuaciones polinómicas son un enunciado que plantea la igualdad de dos expresiones o miembros, donde al menos uno de los términos que conforman cada lado de la igualdad son polinomios P(x). Estas ecuaciones son nombradas según el grado de sus variables.

En general, una ecuación es un enunciado que establece la igualdad de dos expresiones, donde en al menos una de estas se tienen cantidades desconocidas, que son llamadas variables o incógnitas. Aunque existen muchos tipos de ecuaciones, generalmente estas son clasificadas en dos tipos: algebraicas y trascendentes.

Las ecuaciones polinómicas solo contienen expresiones algebraicas, que pueden tener una o más incógnitas que intervienen en la ecuación. Según el exponente (grado) que tengan pueden clasificarse en: primer grado (lineales), segundo grado (cuadráticas), tercer grado (cúbicas), cuarto grado (cuárticas), de grado mayor o igual que cinco e irracionales.

Características de las ecuaciones polinómicas

Las ecuaciones polinómicas son expresiones que están formadas por una igualdad entre dos polinomios; es decir, por las sumas finitas de multiplicaciones entre valores que son desconocidos (variables) y números fijos (coeficientes), donde las variables pueden tener exponentes, y su valor puede ser un número entero positivo, incluyendo el cero.

Los exponentes determinan el grado o tipo de ecuación. Aquel término de la expresión que tenga el exponente de mayor valor representará el grado absoluto del polinomio.

Las ecuaciones polinómicas también son conocidas como algebraicas, sus coeficientes pueden ser números reales o complejos y las variables son números desconocidos representados por una letra, como por ejemplo: “x”.

Si al sustituir un valor por la variable “x” en P(x) el resultado es igual a cero (0), entonces se dice que ese valor satisface la ecuación (es una solución), y generalmente es llamado raíz del polinomio.

Cuando se desarrolla una ecuación polinómica se quieren encontrar todas las raíces o soluciones.

Tipos de ecuaciones polinómicas

Existen varios tipos de ecuaciones polinómicas, que son diferenciadas según el número de variables, y también según su el grado de su exponente.

Así, las ecuaciones polinómicas —donde su primer término es un polinomio que tiene una sola incógnita, considerando que su grado puede ser cualquier número natural (n) y el segundo término es cero—, pueden expresarse de la siguiente manera:

a_{n *} xⁿ + a_{n-1 *} x^n-1 + … + a_{1 *} x¹ + a_{0 *} x₀ = 0

Donde:

• a_n, a_n-1 y a₀, son coeficientes (números) reales.
• a_n es diferente de cero.
• El exponente n es un número entero positivo que representa el grado de la ecuación.
• x es la variable o incógnita que debe ser buscada.

El grado absoluto o mayor de una ecuación polinómica es aquel exponente de mayor valor entre todos aquellos que forman el polinomio; de esa forma, las ecuaciones son clasificadas como:

Primer grado

Las ecuaciones polinómicas de primer grado, también conocidas como ecuaciones lineales, son aquellas en las que el grado (el mayor exponente) es igual a 1, el polinomio es de la forma P(x) = 0; y es compuesta por un término lineal y uno independiente. Se escribe de la siguiente manera:

ax + b = 0.

Donde:

• a y b son números reales y a ≠ 0.
• ax es el término lineal.
• b es el término independiente.

Por ejemplo, la ecuación 13x – 18 = 4x.

Para resolver ecuaciones lineales se deben pasar todos los términos que contengan la incógnita x a un lado de la igualdad, y los que no se tienen se mueven al otro lado, para así despejarla y obtener una solución:

13x – 18 = 4x

13x = 4x + 18

13x – 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

De esa forma, la ecuación dada tiene una sola solución o raíz, que es x=2.

Segundo grado

Las ecuaciones polinómicas de segundo grado, también conocidas como ecuaciones cuadráticas, son aquellas en las que el grado (el mayor exponente) es igual a 2, el polinomio es de la forma P(x) = 0, y está compuesta por un término cuadrático, uno lineal y uno independiente. Se expresa de la siguiente manera:

ax² + bx + c = 0.

Donde:

• a, b y c son números reales y a ≠ 0.
• ax² es el término cuadrático, y “a” es el coeficiente del término cuadrático.
• bx es el término lineal, y “b” es el coeficiente del término lineal.
• c es el término independiente.

Resolvente

Generalmente, la solución a este tipo de ecuaciones es dada al despejar x de la ecuación, y queda de la siguiente forma, la cual es llamada resolvente:

Allí, (b² – 4ac) es llamado discriminante de la ecuación y esta expresión determina el número de soluciones que puede tener la ecuación:

• Si (b² – 4ac) = 0, la ecuación tendrá una única solución que es doble; es decir, tendrá dos soluciones iguales.
• Si (b² – 4ac) > 0, la ecuación tendrá dos soluciones reales distintas.
• Si (b² – 4ac) 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Por ejemplo, se tiene la ecuación 4x² + 10x – 6 = 0, para resolverla primero se identifican los términos a, b y c, y después se sustituye en la fórmula:

a = 4

b = 10

c = -6.

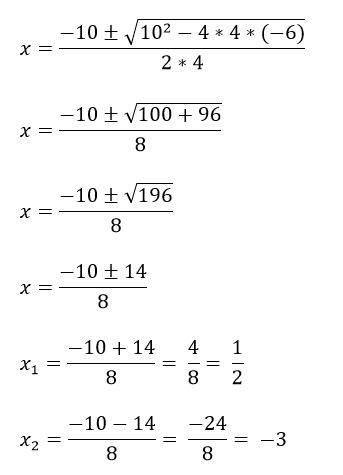
Existen casos en los que las ecuaciones polinómicas de segundo grado no tienen los tres términos, y por eso son solucionadas de diferente manera:

• En el caso de que las ecuaciones cuadráticas no tengan el término lineal (es decir, b = 0), la ecuación estará expresada como ax² + c = 0. Para resolverla se despeja x² y se aplican las raíces cuadradas en cada miembro, recordando que se deben considerar los dos signos posibles que pueda tener la incógnita:

ax² + c = 0.

x² =  – c ÷ a

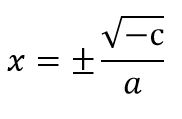
Por ejemplo, 5 x² – 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Cuando la ecuación cuadrática no tenga un término independiente (es decir, c=0), la ecuación estará expresada como ax² + bx = 0. Para resolverla se debe sacar el factor común de la incógnita x en el primer miembro; como la ecuación esta igualada a cero, se cumple que al menos uno de los factores será igual a 0:

ax² + bx = 0.

x(ax + b) = 0.

De esa forma, se tiene que:

x = 0.

x = -b ÷ a.

Por ejemplo: se tiene la ecuación 5x² + 30x = 0. Primero se factoriza:

5x² + 30x = 0

x (5x + 30) = 0.

Se generan dos factores que son x y (5x + 30). Se considera que uno de estos será igual a cero y se le da solución al otro:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Grado mayor

Las ecuaciones polinómicas de grado mayor son aquellas que van desde el tercer grado en adelante, que pueden ser expresadas o resueltas con la ecuación polinómica general para un grado cualquiera:

a_{n *} xⁿ + a_{n-1 *} x^n-1 + … + a_{1 *} x¹ + a_{0 *} x₀ = 0

Esta es utilizada porque una ecuación con un grado mayor a dos es el resultado de la factorización de un polinomio; es decir, esta expresada como la multiplicación de polinomios de grado uno o mayor, pero sin raíces reales.

La solución de este tipo de ecuaciones es directa, porque la multiplicación de dos factores será igual a cero si alguno de los factores es nulo (0); por lo tanto, se debe resolver cada una de las ecuaciones polinómicas halladas, igualando cada uno de sus factores a cero.

Por ejemplo, se tiene la ecuación de tercer grado (cúbica) x³ + x² +4x + 4 = 0. Para resolverla se tienen que seguir los siguientes pasos:

• Se agrupan los términos:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Se descomponen los miembros para sacar el factor común de la incógnita:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• De esa forma se obtienen dos factores, que deben ser igualados a cero:

(x² + 4) = 0

(x + 1) = 0.

• Se puede observar que el factor (x² + 4) = 0 no va a tener una solución real, mientras que el factor (x + 1) = 0 sí. Por lo tanto, la solución es:

(x + 1) = 0

x = -1.

Ejercicios resueltos

Resolver las siguientes ecuaciones:

Primer ejercicio

(2x² + 5)_*(x – 3)_*(1 + x) = 0.

Solución

En este caso la ecuación está expresada como la multiplicación de polinomios; es decir, se encuentra factorizada. Para resolverla se debe igualar cada factor a cero:

2x² + 5 = 0, no tiene solución.

x – 3 = 0

x = 3.

1 + x = 0

x = – 1.

De esa forma, la ecuación dada tiene dos soluciones: x = 3 y x = -1.

Segundo ejercicio

x⁴ – 36 = 0.

Solución

Fue dado un polinomio, que puede ser rescrito como una diferencia de cuadrados para llegar a una solución más rápida. Así, la ecuación queda:

(x² + 6)_*( x² – 6) = 0.

Para encontrar la solución de las ecuaciones se igualan ambos factores a cero:

(x² + 6) = 0, no tiene solución.

(x² – 6) = 0

x² = 6

x = ±√6.

Así, la ecuación inicial tiene dos soluciones:

x = √6.

x = – √6.