¿Cómo sacar el ángulo de un triángulo? (Ejemplo)

Existen diversas maneras de calcular los lados y los ángulos de un triángulo. Estas dependen del tipo de triángulo con el que se esté trabajando.

En esta oportunidad, se mostrará cómo calcular los lados y los ángulos de un triángulo rectángulo, suponiendo que ciertos datos del triángulo con conocidos.

Los elementos que se utilizarán son:

– El teorema de Pitágoras

Dado un triángulo rectángulo con catetos “a”, “b” e hipotenusa “c”, se cumple que “c²=a²+b²”.

– Área de un triángulo

La fórmula para calcular el área de cualquier triángulo es A=(b×h)/2, donde “b” es la longitud de la base y “h” la longitud de la altura.

– Ángulos de un triángulo

La suma de los tres ángulos internos de un triángulo es 180°.

– Las funciones trigonométricas:

Considérese un triángulo rectángulo. Entonces, se definen las funciones trigonométricas seno, coseno y tangente del ángulo beta (β) como sigue:

sen(β) = CO/Hip,  cos(β)= CA/Hip y tan(β)=CO/CA.

¿Cómo calcular los lados y los ángulos de un triángulo rectángulo?

Dado un triángulo rectángulo ABC, se pueden presentar las siguientes situaciones:

1- Son conocidos los dos catetos

Si el cateto “a” mide 3 cm y el cateto “b” mide 4 cm, entonces para calcular el valor de “c” se utiliza el teorema de Pitágoras. Al sustituir los valores de “a” y “b” se obtiene que c²=25 cm², lo cual implica que c=5 cm.

Ahora, si el ángulo β es opuesto al cateto “b”, entonces sen(β)=4/5. Al aplicar la función inversa del seno, en esta última igualdad se obtiene que β=53,13º. Ya son conocidos dos ángulos internos del triángulo.

Sea θ el ángulo que falta por conocer, entonces 90º+53,13º+θ=180°, de donde se obtiene que θ=36,87º.

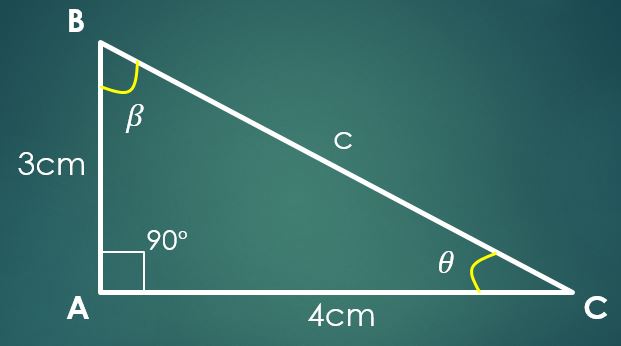
En este caso no es necesario que los lados conocidos sean los dos catetos, lo importante es conocer el valor de dos lados cualesquiera.

2- Es conocido un cateto y el área

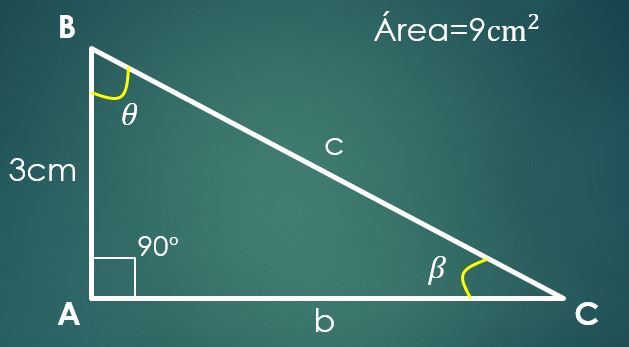
Sea a=3 cm el cateto conocido y A=9 cm² el área del triángulo.

En un triángulo rectángulo un cateto puede ser considerado como base y el otro como altura (dado que son perpendiculares).

Supongamos que “a” es la base, por lo tanto, 9=(3×h)/2, de donde se obtiene que el otro cateto mide 6 cm. Para calcular la hipotenusa se procede como en el caso anterior, y se obtiene que c=√45 cm.

Ahora, si el ángulo β es opuesto al cateto “a”, entonces sen(β)=3/√45. Al despejar β se obtiene que su valor es 26,57º. Solo falta conocer el valor del tercer ángulo θ.

Se cumple que 90°+26,57º+θ=180°, de donde se concluye que θ=63,43º.

3- Es conocido un ángulo y un cateto

Sea β=45° el ángulo conocido y a=3 cm el cateto conocido, donde el cateto “a” es opuesto al ángulo β. Usando la fórmula de la tangente, se obtiene que tg(45°)=3/CA, de donde resulta que CA=3 cm.

Usando el teorema de Pitágoras se obtiene que c²=18 cm², es decir, c=3√2 cm.

Se sabe que un ángulo mide 90° y que β mide 45°, de aquí se concluye que el tercer ángulo mide 45°.

En este caso, el lado conocido no tiene por qué ser un cateto, puede ser cualquiera de los tres lados del triángulo.