Círculo unitario: funciones trigonométricas y aplicaciones
El círculo unitario es un círculo de radio igual a 1, que por lo general está centrado en el punto (0,0) del sistema de coordenadas cartesianas xy. Se emplea para definir fácilmente las razones trigonométricas de los ángulos mediante triángulos rectángulos.
La ecuación del círculo unitario centrado en el origen es:
x2 + y2 = 1
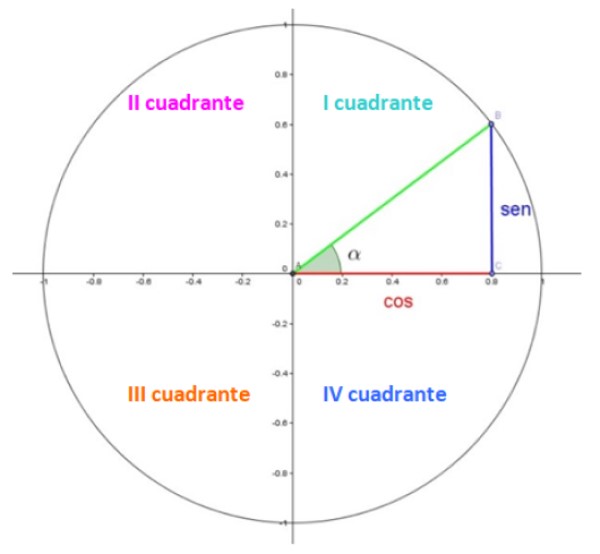
En la figura 1 tenemos el círculo unitario, en el que cada cuarto está en un cuadrante. Los cuadrantes se numeran con números romanos y se cuentan en sentido antihorario.
En el primer cuadrante hay un triángulo. Los catetos, en rojo y en azul miden respectivamente 0.8 y 0.6, mientras que la hipotenusa en verde mide 1, pues es un radio.
El ángulo agudo α es un ángulo central en posición estándar, lo cual significa que su vértice coincide con el punto (0,0) y su lado inicial con el eje x positivo. El ángulo se mide en sentido contrario al de las manecillas del reloj y por convención se le asigna signo positivo.
Pues bien, en el círculo unitario, las coordenadas de coseno y seno de α son respectivamente las coordenadas x e y del punto B, que en el ejemplo mostrado son 0.8 y 0.6.
A partir de estas dos se definen:
- tg α = sen α/cos α = 0.6/0.8 = 0.75
- sec α = 1/ cos α = 1/0.8 = 1.25
- cosec α = 1 / sen α = 1/0.6 = 1.66…
- ctg α = 1/tg = 0.8/0.6 = 1.33…
Índice del artículo
- 1 Aplicaciones del círculo unitario
- 2 Trazado de las gráficas de coseno y seno
- 3 Ejercicios resueltos
- 4 Referencias
Si nos limitamos a los triángulos rectángulos, las razones trigonométricas se aplicarían únicamente a los ángulos agudos. Sin embargo, con ayuda del círculo unitario, se extiende el cálculo de las razones trigonométricas a cualquier ángulo α.
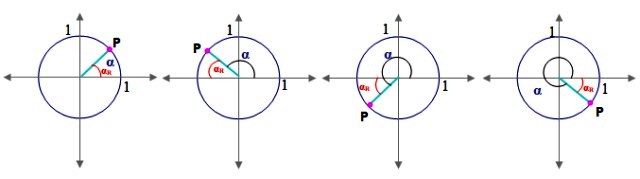
Para ello se requiere definir en primer lugar el concepto de ángulo de referencia αR:
Sea α un ángulo en posición estándar (aquel cuyo lado inicial coincide con el eje x positivo), su ángulo de referencia αR está entre su lado terminal y el eje x. La figura 2 muestra el ángulo de referencia para ángulos en I, II, III y IV cuadrante.
Para cada cuadrante, el ángulo de referencia se calcula así:
-Primer cuadrante: αR = α
-Segundo cuadrante: αR = 180º – α
-Tercer cuadrante: αR = α – 180º
-Cuarto cuadrante: αR = 360º – α
Nótese que el primer cuadrante el ángulo α coincide con su ángulo de referencia. Pues bien, las razones trigonométricas del ángulo α son las mismas de su ángulo de referencia, con los signos de acuerdo a los que tengan los cuadrantes en que caiga el lado terminal de α.
En otras palabras, las razones trigonométricas coseno y seno del ángulo α coinciden con las coordenadas del punto P, de acuerdo a la figura 2.
En la siguiente figura vemos las razones trigonométricas de algunos ángulos notables, tal como se deducen a partir del círculo unitario.
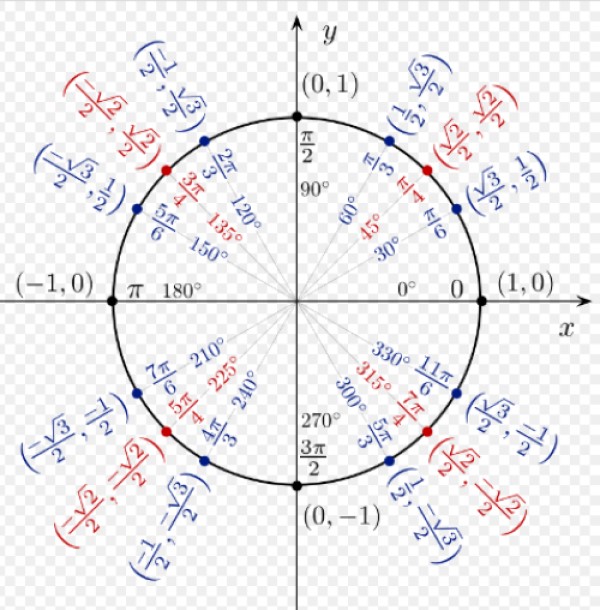
Las razones coseno y seno de cualquier ángulo en el I cuadrante son todas positivas. Para α = 60º tenemos las coordenadas (1/2; √3/2), que corresponden respectivamente a cos 60º y sen 60º.
Las coordenadas de α = 120º son (-1/2; √3/2), ya que al encontrarse en el segundo cuadrante, la coordenada x es negativa.
Con ayuda del círculo unitario y las coordenadas de los puntos P sobre él, es posible trazar las gráficas de las funciones cos t y sen t, como veremos a continuación.
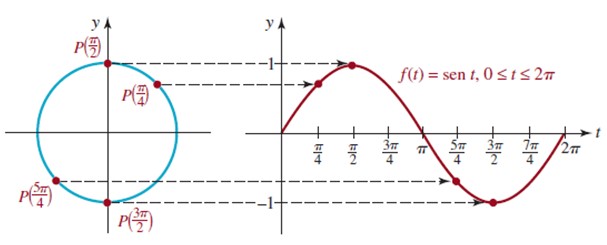
Para ello se ubican varias posiciones del punto P(t) en el círculo unitario. Comenzaremos por la gráfica de la función f(t) = sen t.
Podemos observar que cuando vamos desde t = 0 hasta t = π/2 (90º) el valor de sen t va aumentando hasta llegar a 1, que es el valor máximo.
En cambio, desde t= π/2 hasta t = 3π/2 el valor de sen t disminuye desde 1, pasando por 0 en t = π hasta llegar a su mínimo de -1 en t = 3π/2.
En la figura se muestra la gráfica del primer ciclo de f(t) = sen t que corresponde con la primera vuelta al círculo unitario, dicha función es periódica de período 2π.
Se puede llevar a cabo un procedimiento análogo para obtener la gráfica de la función f(t) = cos t, como se muestra en la siguiente animación:
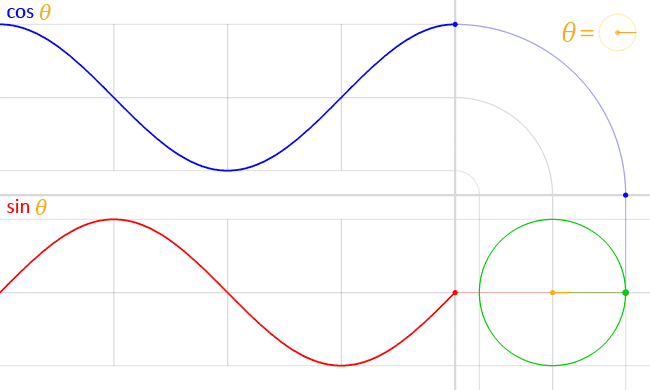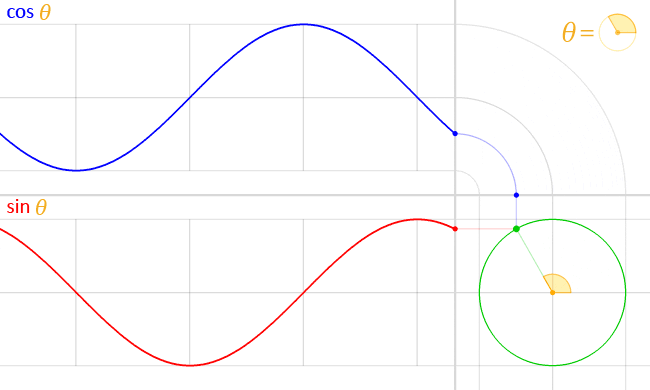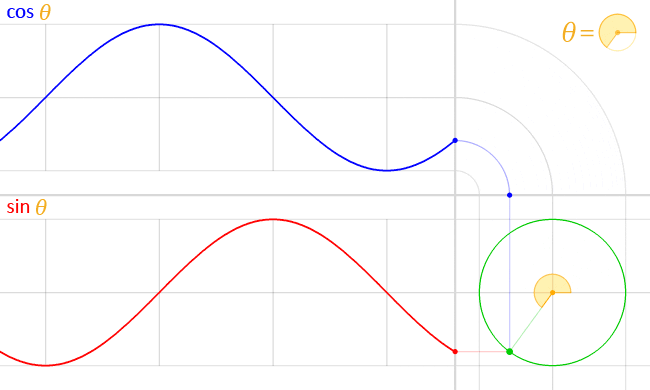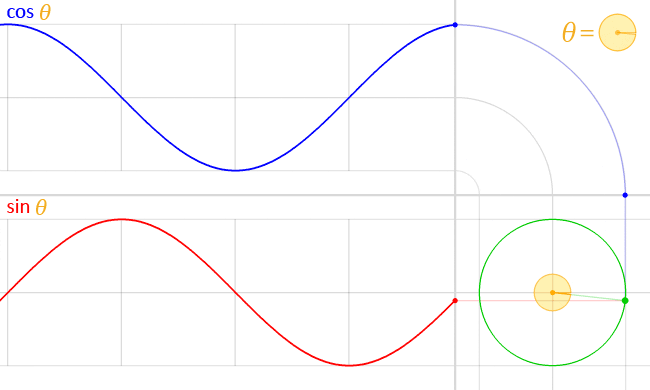
-Ambas funciones son continuas en el conjunto de los números reales y además periódicas, de período 2π.
-El dominio de las funciones f (t) = sen t y f(t) = cos t son todos los números reales: (-∞,∞).
-Para el rango o recorrido de seno y coseno se tiene el intervalo [-1,1]. Los corchetes indican que -1 y 1 están incluidos.
– Los ceros de sen t son los valores que corresponden a nπ con n entero, mientras que los ceros de cos t son [(2n+1)/2] con n también entero.
-La función f(t) = sen t es impar, tiene simetría respecto al origen mientras que la función cos t es par, su simetría es respecto al eje vertical.
Dado cos t = – 2/5, que es la coordenada horizontal del punto P(t) en el círculo unitario en el segundo cuadrante, obtener la correspondiente coordenada vertical sen t.
Solución
Puesto que P(t) pertenece al círculo unitario, en el cual se cumple que:
x2 + y2 = 1
Por lo tanto:
y = ±√ 1 – x2
Ya que P(t) se encuentra en el segundo cuadrante se tomará el valor positivo. La coordenada vertical del punto P(t) es y:
y = √ 1 – (-2/5)2 = √0.84
Un modelo matemático para la temperatura T en grados Fahrenheit en un día cualquiera, t horas después de la medianoche, viene dado por:
T (t) = 50 + 10 sen [(π /12) × (t – 8)]
Con t comprendido entre 0 y 24 horas. Hallar:
a) La temperatura a las 8 am.
b) Horas durante las cuales T (t) = 60 ºF
c) Temperaturas máxima y mínima.
Solución a
Sustituimos t = 8 en la función dada:
T (8) = 50 + 10 sen [(π/12)×(t-8)] = 50 + 10 sen [(π/12)×(8-8)] =
= 50 + 10 x sen 0 = 50 ºF
Solución b
50 + 10 sen [(π/12)×(t-8)] = 60
Es una ecuación trigonométrica y hay que despejar la incógnita “t”:
10 sen [(π/12)×(t-8)] = 60 – 50 = 10
sen [(π/12)×(t-8)] = 1
Sabemos que sen π/2 = 1, por lo tanto el argumento del seno tiene que ser 1:
(π/12)×(t-8) = π/2
t-8 = 6
t = 14 h
Se concluye que a 14 horas después de medianoche la temperatura es de 60 º, es decir, las 2 pm. No hay otra hora a lo largo del día (24 horas) en que esto suceda.
Solución c
La temperatura máxima corresponde al valor en el cual sen [(π/12)×(t-8)] = 1 y es de 60 ºF. En cambio la mínima ocurre si sen [(π/12)×(t-8)] = -1 y es de 40 ºF.
- Figuera, J. 1999. Matemática. 1ro. Diversificado. Ediciones Colegial Bolivariana.
- Hoffman, J. Selección de temas de Matemática. Volumen 4.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Math is Fun. Unit Circle. Recuperado de: de: mathsisfun.com.
- Wikipedia. Identidades y fórmulas de trigonometría. Recuperado de: es.wikipedia.org.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
