Distribución uniforme continua: características, ejemplos, aplicaciones
Una variable aleatoria tiene una distribución uniforme continua si la probabilidad de que tome un valor, dentro de un intervalo finito [a,b], es la misma para cualquier sub-intervalo de igual longitud.
Esta distribución es análoga a la distribución uniforme discreta, que asignaba a cada resultado del experimento aleatorio la misma probabilidad, pero en este caso la variable a considerar es continua. Por ejemplo, el experimento que consiste en seleccionar un número real al azar, entre los valores a y b, sigue la distribución uniforme. Acá se tiene su gráfica:
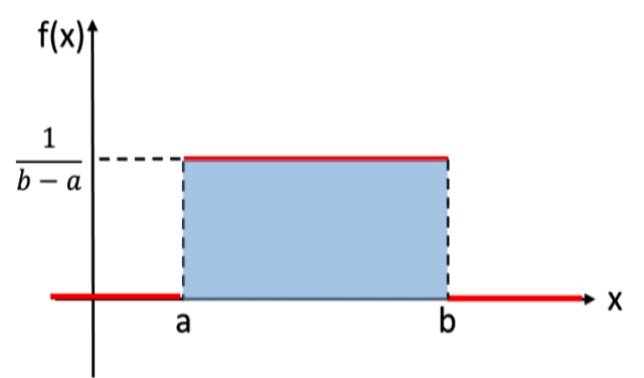
En notación matemática, la distribución uniforme continua tiene una función de densidad definida como una función a trozos o por tramos, que se puede escribir como:
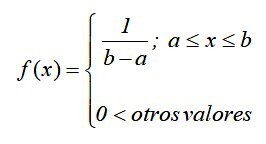
La gráfica de esta función, conocida como curva o función de densidad, es un rectángulo, por ello la distribución uniforme continua se conoce también como distribución rectangular y es la más simple de las distribuciones continuas.
El área bajo la gráfica de una distribución de probabilidades es igual a 1 y toma siempre valores positivos. La distribución uniforme cumple con estos criterios. No es necesario integrar directamente para comprobar que el área es 1, ya que el área del rectángulo sombreado en la figura 1 se puede calcular mediante la fórmula:
Área = base x altura = (b−a) x [1/(b−a)] = 1
Conocer el área bajo la curva de densidad es muy importante, porque hay una relación entre el área y la probabilidad de ocurrencia de un evento, que para esta distribución se determina en el siguiente apartado.
Características de la distribución uniforme continua
La distribución uniforme continua se caracteriza por su:
Función de densidad
Sea X la variable aleatoria continua, que pertenece al intervalo [a,b], entonces:
Función de distribución
Mediante la función de distribución se calcula la probabilidad de que la variable aleatoria X tome un valor x de entre los posibles valores del intervalo [a,b]. Para una distribución continua, en general se calcula de esta manera:
En el caso de la distribución uniforme continua, dicha probabilidad F(x) equivale al área del rectángulo cuya base es (x-a) y su altura es (b-a):
Matemáticamente, si F(x) = Pr (X=x) se establece la siguiente función por partes, de acuerdo al resultado anterior:
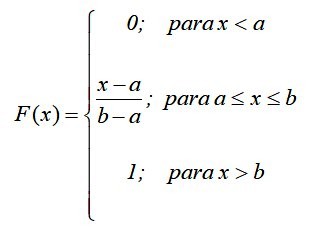
De esta manera se comprueba lo dicho antes: la probabilidad únicamente depende del valor de (x-a) y no de su ubicación en el intervalo [a,b]. La gráfica de la función de distribución es:
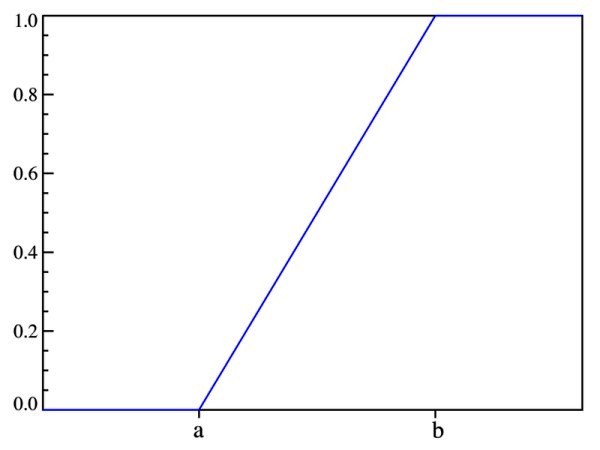
Valor esperado, varianza y desviación estándar
Luego de hacer numerosos experimentos con la variable aleatoria continua, su valor promedio se denomina valor esperado, se denota como E(X) y se calcula mediante la siguiente integral:
V(X) = E(X2) – E(X)2
Por lo tanto:
D(X) = √ V(X)
Mediana, moda, simetría y curtosis
Se puede comprobar fácilmente que la mediana, que es el valor central de la distribución uniforme, es igual a la media, y como no hay un valor que se repita más que otros, ya que todos son igualmente probables en el intervalo [a,b], la moda no existe.
En cuanto a la simetría, la distribución uniforme es simétrica y la curtosis, que es el grado en que concentran los valores alrededor del centro es -6/5.
Ejemplos
Diversas situaciones se pueden modelar mediante la distribución continua, y así predecir su comportamiento. A continuación se muestran algunos ejemplos:
Ejemplo 1
Una compañía que brinda servicio eléctrico provee niveles de voltajes uniformemente distribuidos, entre 123.0 V y 125.0 V. Esto significa que en la toma doméstica es posible obtener cualquier valor de voltaje que pertenezca a dicho intervalo.
Entonces, según lo visto anteriormente, la gráfica de la función de densidad es el rectángulo en rojo:
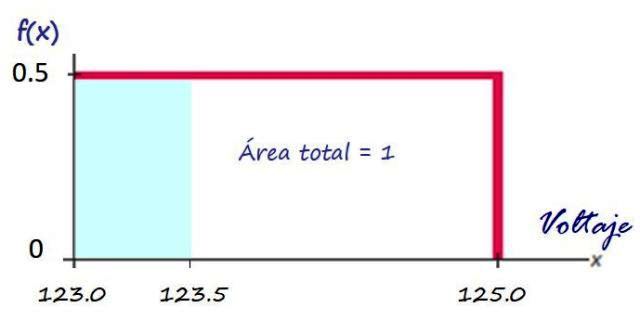
Calcular la probabilidad de tener un voltaje dentro del intervalo dado es muy fácil, por ejemplo ¿cuál es la probabilidad de que la compañía envíe un voltaje menor a 123.5 V?
Esta probabilidad equivale al área del rectángulo sombreado en azul:
P(X123.5) = (123.5 −123.0)x 0.5 = 0.25
Y ¿cuál es la probabilidad de que el voltaje entregado sea mayor que 124.0 V?
Como el área total es igual a 1, la probabilidad buscada es:
P (X>124.0 V) = 1 – (1×0.5) = 0.5
Tiene sentido, ya que 124.0 es precisamente el valor en el centro del intervalo.
Ejemplo 2
Cierta variable aleatoria X tiene una distribución uniforme en el intervalo [0,100]. Determinar:
a) La probabilidad de que el valor de X sea menor que 22.
b) La probabilidad de que X tome valores entre 20 y 35.
c) El valor esperado, la varianza y la desviación estándar de esta distribución.
Respuesta a
Se determina de modo semejante al ejemplo anterior, pero antes hay que determinar la altura del rectángulo, recordando que el área total debe ser igual a 1:
Área = 100 × altura = 1
Por lo tanto el rectángulo tiene una altura igual a 1/100 = 0.01
P(X22) = 22×0.01 = 0.22
Respuesta b
La probabilidad pedida equivale al área del rectángulo cuyo ancho es (35 – 20) y cuya altura es 0.01:
P (22 Si se prefiere acudir directamente a la función de distribución dada anteriormente, entonces solo hay que sustituir los valores en: P(20≤X≤35) =F(35)-F(20) Con F(x) dada por: F (x) = (x-a) / (b-a) Los valores a introducir son: a = 0 b= 100 F (35) = (35-0) / (100-0)=0.35 F (20) = (20-0) / (100-0)=0.20 P(20≤X≤35) =0.35-0.20 = 0.15 El valor esperado es: E(X)= (a+b)/2 = (100+0)/2 = 50 La varianza es: V(X)=(b-a)2/12= (100-0)2/12 = 833.33 Y la desviación estándar es: D(X) = √833.33 = 28.87 Esta distribución es útil cuando se llevan a cabo procesos de simulación estadística o al trabajar en eventos cuya frecuencia de aparición es regular. Algunos lenguajes de programación generan números aleatorios entre 0 y 1, y como se puede observar de los ejemplos anteriores, la distribución de probabilidades seguida es uniforme. En este caso el intervalo a considerar es el [0,1]. Si se tiene un experimento en el cual los eventos tienen regularidad, tal como se explicó antes, se puede, en principio, asignar a cada uno la misma probabilidad de ocurrencia. En tal caso el modelo probabilístico de distribución uniforme brinda información para el análisis. La distribución uniforme también se emplea en el redondeo de las diferencias entre los valores observados y los valores reales de una variable, suponiendo una distribución uniforme del error en un intervalo dado, según el redondeo, usualmente de -0,5 a +0,5.Respuesta c
Aplicaciones
Generación de números aleatorios
Muestreo de distribuciones arbitrarias
Redondeo de errores
Referencias
