Magnitud vectorial: qué es, significado, elementos, ejemplos
¿Qué es una magnitud vectorial?
Una magnitud vectorial es toda expresión representada por un vector que posee valor numérico (módulo), dirección, sentido y punto de aplicación. Algunos ejemplos de magnitudes vectoriales son el desplazamiento, la velocidad, la fuerza y el campo eléctrico.
La representación gráfica de una magnitud vectorial consiste en una flecha cuya punta indica su dirección y sentido, su longitud es el módulo y el punto de inicio es el origen o punto de aplicación.
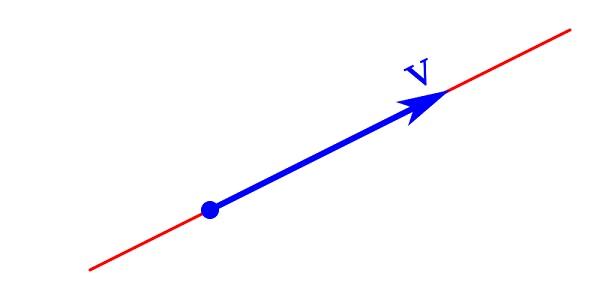
La magnitud vectorial se representa analíticamente con una letra que lleva una flecha en la parte superior apuntando hacia la derecha en dirección horizontal. También puede ser representada por una letra escrita en negrita V cuyo módulo ǀVǀ se escribe en letra cursiva V.
Una de las aplicaciones del concepto de magnitud vectorial es en el diseño de autopistas y carreteras, específicamente en el diseño de sus curvaturas. Otra aplicación es el cálculo del desplazamiento entre dos lugares o el cambio de velocidad de un vehículo.
Elementos de una magnitud vectorial
Una magnitud vectorial es toda entidad representada por un segmento de recta, con orientación en el espacio, que posee las características propias de un vector. Sus elementos son:
Módulo: Es el valor numérico que indica el tamaño o la intensidad de la magnitud vectorial.
Dirección: Es la orientación del segmento de recta en el espacio que lo contiene. El vector puede tener dirección horizontal, vertical o inclinada; norte, sur, este u oeste; noreste, sureste, suroeste o noroeste.
Sentido: Se indica con la punta de la flecha en el extremo del vector.
Punto de aplicación: Es el origen o punto de actuación inicial del vector.
Clasificación de vectores
Los vectores se clasifican en colineales, paralelos, perpendiculares, concurrentes, coplanarios, libres, deslizantes, opuestos, equipolentes, fijos y unitarios.
Colineales: Pertenecen o actúan sobre una misma línea recta, también se les llama linealmente dependientes y pueden ser verticales, horizontales e inclinados.
Paralelos: Tienen la misma dirección o inclinación.
Perpendiculares: dos vectores son perpendiculares entre sí cuando el ángulo entre ellos es 90°.
Concurrentes: Son vectores que al deslizarse sobre su línea de acción coinciden en un mismo punto del espacio.
Coplanarios: Actúan en un plano, por ejemplo el plano xy.
Libres: Se trasladan en cualquier punto del espacio manteniendo su módulo, dirección y sentido.
Deslizantes: Se trasladan a lo largo de la línea de acción determinada por su dirección.
Opuestos: Tienen el mismo módulo y dirección, y el sentido contrario.
Equipolentes: Tienen el mismo módulo, dirección y sentido.
Fijos: Tienen invariable el punto de aplicación.
Unitarios: Vectores cuyo módulo es la unidad.
Componentes vectoriales
Una magnitud vectorial en un espacio tridimensional se representa en un sistema de tres ejes perpendiculares entre sí (x,y,z) llamado triedro ortogonal.
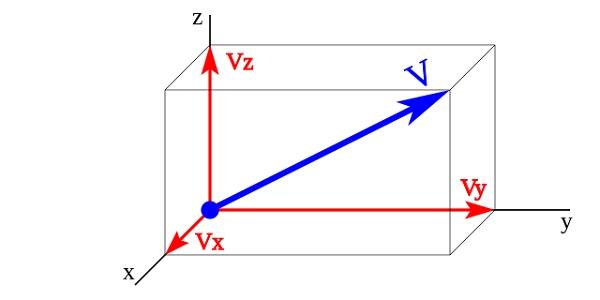
En la imagen los vectores Vx, Vy, Vz son las componentes vectoriales del vector V cuyos vectores unitarios son x,y,z. La magnitud vectorial V se representa por la suma de sus componentes vectoriales.
V =Vx + Vy + Vz
La resultante de varias magnitudes vectoriales es la suma vectorial de todos los vectores y reemplaza a dichos vectores en un sistema.
Campo vectorial
El campo vectorial es la región del espacio en el cual en cada uno de sus puntos le corresponde una magnitud vectorial. Si la magnitud que se manifiesta es una fuerza actuando sobre un cuerpo o sistema físico entonces el campo vectorial es un campo de fuerzas.
El campo vectorial se representa gráficamente mediante líneas de campo que son líneas tangentes de la magnitud vectorial en todos los puntos de la región. Algunos ejemplos de campos vectoriales son el campo eléctrico creado por una carga eléctrica puntual en el espacio y el campo de velocidades de un fluido.

Operaciones con vectores
Adición de vectores: Es la resultante de dos o más vectores. Si se tienen dos vectores O y P la suma es O + P = Q. El vector Q es el vector resultante que se obtiene gráficamente trasladando el origen del vector A al extremo del vector B.
Sustracción de vectores: La sustracción de dos vectores O y P es O – P = Q. El vector Q se obtiene sumando al vector O su opuesto –P. El método gráfico es el mismo de la suma con la diferencia de que se traslada al extremo el vector opuesto.
Producto escalar: El producto de una magnitud escalar a por una magnitud vectorial P es un vector mP que tiene la misma dirección del vector P. Si la magnitud escalar es nula el producto escalar es un vector nulo.
Ejemplos de magnitudes vectoriales
Posición
La posición de un objeto o partícula con respecto a un sistema de referencia es un vector que viene dado por sus coordenadas rectangulares x, y, z, y se representa mediante sus componentes vectoriales xî, yĵ, zk. Los vectores î, ĵ, k son vectores unitarios.
Una partícula en un punto (x,y,z) tiene un vector de posición r = xî + yĵ + zk. El valor numérico del vector posición es r= √(x2 + y2 + z2). El cambio de posición de la partícula desde una posición a otra con respecto a un sistema de referencia es el vector Desplazamiento Δr y se calcula con la siguiente expresión vectorial:
Δr = r2 – r1
Aceleración
La aceleración media (am) se define como la variación de la velocidad v en un intervalo de tiempo Δt y la expresión para calcularla es am=Δv/Δt, siendo Δv el vector cambio de velocidad.
La aceleración instantánea (a) es el límite de la aceleración media am cuando Δt se hace tan pequeño que tiende a cero. La aceleración instantánea se expresa en función de sus componentes vectoriales
a =axî +ay ĵ+ azk
Campo gravitacional
La fuerza de atracción gravitacional que ejerce una masa M, situada en el origen, sobre otra masa m en un punto del espacio x, y, z es un campo vectorial llamado campo de fuerza gravitacional. Esta fuerza viene dada por la expresión:
F=(-mMG/r)ȓ
r = xî + yĵ + zk
F = es la magnitud física fuerza gravitacional
G = es la constante de gravitación Universal
ȓ = es el vector de posición de la masa m
Referencias
- Tallack, J C. Introduction to Vector Analysis. Cambridge : Cambridge University Press, 2009.
- Spiegel, M R, Lipschutz, S y Spellman, D. Vector Analysis. s.l. : Mc Graw Hill, 2009.
- Brand, L. Vector Analysis. New York : Dover Publications, 2006.
- Griffiths, D J. Introduction to Electrodynamics. New Jersey : Prentice Hall, 1999. págs. 1-10.
- Hague, B. An Introduction to Vector Analysis. Glasgow : Methuen & Co. Ltd, 2012.
