Movimiento rectilíneo uniformemente acelerado: características, fórmulas
El movimiento rectilíneo uniformemente acelerado es aquel que transcurre sobre una línea recta y en el cual el móvil aumenta o disminuye su velocidad a una tasa constante. Dicha tasa es la magnitud que describe el ritmo con que la velocidad cambia y se llama aceleración.
En el caso del movimiento rectilíneo uniformemente acelerado o variado (MRUV), la aceleración constante se encarga de cambiar la magnitud de la velocidad. En otros tipos de movimiento, la aceleración también es capaz de cambiar la dirección y el sentido de la velocidad, o incluso cambiar únicamente la dirección, como en el movimiento circular uniforme.

Puesto que la aceleración representa el cambio de la velocidad en el tiempo, sus unidades en el Sistema Internacional son m/s2 (metros sobre segundos al cuadrado). Al igual que la velocidad, a la aceleración se le pueden adjudicar signo positivo o negativo, según aumente o disminuya la velocidad.
Una aceleración digamos de +3 m/s2 significa que por cada segundo que transcurre, la velocidad del móvil aumenta en 3 m/s. Si al comienzo del movimiento (en t= 0) la velocidad del móvil era de +1 m/s, entonces al cabo de un segundo será de 4 m/s y al cabo de 2 segundos será de 7 m/s.
En el movimiento rectilíneo uniformemente variado se toman en cuenta las variaciones de la velocidad que los objetos móviles cotidianamente experimentan. Se trata de un modelo más realista que el del movimiento rectilíneo uniforme. Aún así todavía es bastante limitado, pues restringe al móvil a viajar únicamente sobre una línea recta.
Índice del artículo
Estas son las principales características del movimiento rectilíneo uniformemente acelerado:
-El movimiento siempre transcurre a lo largo de una línea recta.
-La aceleración del móvil es constante, tanto en magnitud como en dirección y sentido.
-La velocidad del móvil aumenta (o disminuye) linealmente.
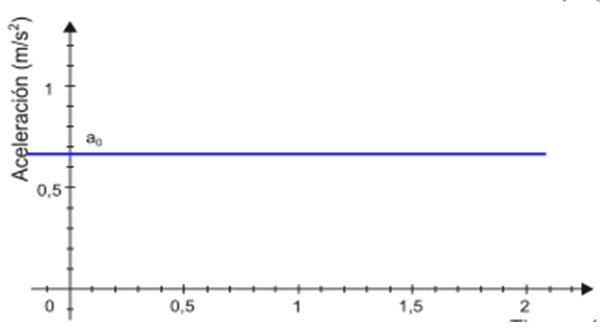
-Dado que la aceleración a se mantiene constante en el tiempo t, la gráfica de su magnitud en función del tiempo es una línea recta. En el ejemplo mostrado en la figura 2, la recta es de color azul y el valor de la aceleración se lee sobre el eje vertical, aproximadamente +0.68 m/s2.
-El gráfico de la velocidad v respecto a t es una línea recta (en color verde en la figura 3), cuya pendiente equivale a la aceleración del móvil. En el ejemplo la pendiente es positiva.
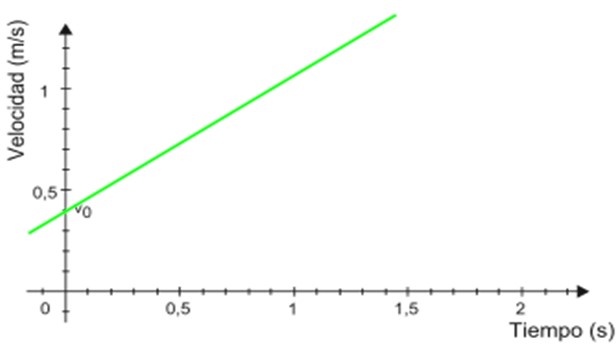
-El corte con el eje vertical indica la velocidad inicial, en este caso es 0.4 m/s.
-Finalmente el gráfico de la posición x versus el tiempo es la curva mostrada en rojo en la figura 4, que siempre es una parábola.
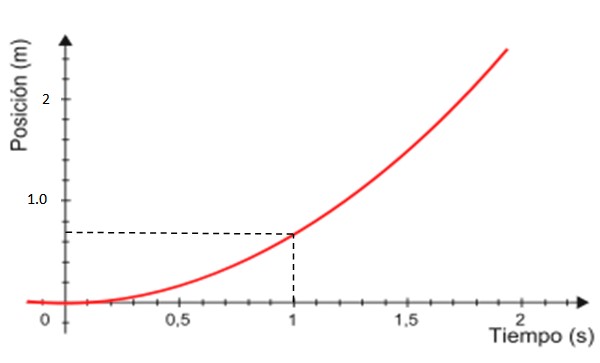
Al disponer de la gráfica v vs. t, el cálculo de la distancia recorrida por el móvil es muy fácil. La distancia recorrida equivale al área bajo la recta que está comprendida dentro del intervalo de tiempo deseado.
En el ejemplo mostrado, supongamos que se desea saber la distancia recorrida por el móvil entre 0 y 1 segundo. Mediante el uso de esta gráfica, ver la figura 5.
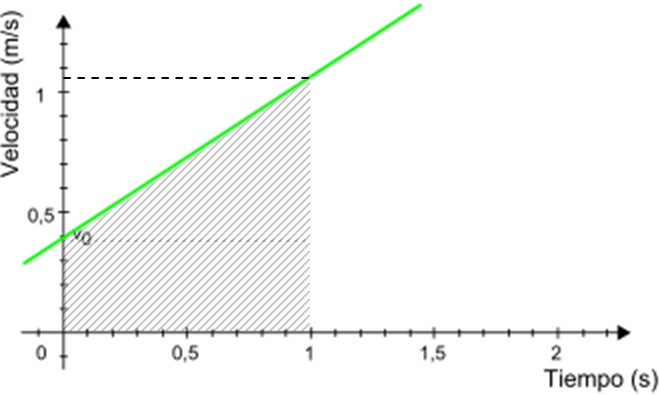
La distancia buscada equivale numéricamente al área del trapecio sombreado en la figura 3. El área del trapecio viene dada por: (base mayor + base menor) x altura/2
Distancia recorrida = (0.4 + 1.05) x 1/ 2 m = 0.725 m
También es posible dividir el área sombreada en un triángulo y un rectángulo, calcular las áreas correspondientes y sumarlas. La distancia recorrida es positiva, aunque la partícula vaya hacia la derecha o hacia la izquierda.
Tanto la aceleración media como la aceleración instantánea tienen el mismo valor en el MRUV, por lo tanto:
-Aceleración: a = constante
Cuando la aceleración es igual a 0 el movimiento es rectilíneo uniforme, ya que la velocidad sería constante en este caso. El signo de a puede ser positivo o negativo.
Ya que la aceleración es la pendiente de la recta v versus t, la ecuación v(t) es:
-Velocidad en función del tiempo: v (t) = vo + at
Donde vo es el valor de la velocidad inicial del móvil
-Posición en función del tiempo: x (t) = xo + vo t +½at2
Cuando no se dispone del tiempo, pero en cambio se tienen velocidades y desplazamientos, hay una ecuación muy útil que se obtiene despejando el tiempo de v (t) = vo + at y sustituyéndolo en la última ecuación. Se trata de:
–Ecuación que no contiene el tiempo: v2 =vo2 +2.a.Δx
Al momento de resolver un ejercicio de cinemática es importante asegurarse de que la situación planteada se adapta al modelo que se va a utilizar. Por ejemplo las ecuaciones del movimiento rectilíneo uniforme no son válidas para un movimiento acelerado.
Y las del movimiento acelerado no son válidas para un movimiento de tipo circular o curvilíneo, por ejemplo. El primero de estos ejercicios resueltos a continuación combina dos móviles con movimientos diferentes. Para resolverlo correctamente, es preciso acudir al modelo de movimiento apropiado.
Para averiguar la profundidad de un pozo, un niño deja caer una moneda y al mismo tiempo activa su cronómetro, el cual detiene justamente al escuchar el golpe de la moneda contra el agua. Su lectura fue de 2.5 segundos. Sabiendo que la rapidez del sonido en el aire es 340 m/s, calcular la profundidad del pozo.
Solución
Sea h la profundidad del pozo. La moneda recorre esta distancia en caída libre, un movimiento vertical uniformemente variado, con velocidad inicial 0, ya que la moneda se deja caer, y aceleración constante hacia abajo igual a 9.8 m/s2. Toma un tiempo tm en hacer esto.
Una vez que la moneda choca contra el agua, el sonido causado por el chasquido viaja hacia arriba hasta el oído del niño, quien detiene el cronómetro al escucharlo. No hay razones para creer que la rapidez del sonido cambie mientras sube por el pozo, así que el movimiento del sonido es rectilíneo uniforme. El sonido tarda un tiempo ts en llegar al niño.
Ecuación de movimiento para la moneda:
h = ½.g.tm2 =4.9 tm2
Donde se han sustituido x y a de la ecuación para la posición dada en el apartado anterior, por h y g.
Ecuación de movimiento para el sonido:
h = vs . ts = 340 ts
Se trata de la familiar ecuación distancia = velocidad x tiempo. Con estas dos ecuaciones se tienen tres incógnitas: h, tm y ts. Para los tiempos hay una relación, se sabe que todo tarda 2.5 segundos en suceder, por lo tanto:
tm + ts = 2.5 s
Igualando ambas ecuaciones:
4.9 tm2 = 340 ts
Despejando uno de los tiempos y sustituyendo:
4.9 tm2=340.(2.5 – tm)
Al desarrollar el término de la derecha y trasponer términos se obtiene:
4.9 tm2+340 tm – 850 = 0
Esta es una ecuación de segundo grado con dos soluciones: 2.416 y -71.8. Se escoge la solución positiva, que es la que tiene sentido, ya que el tiempo no puede ser negativo y en todo caso debe ser menor que 2.5 segundos. Para este tiempo se obtiene al sustituir la profundidad del pozo:
4.9 tm2= 4.9 x 2.4162 m = 28.6 m
Un automóvil que viaja a 90 km/h se acerca a una avenida transversal con un semáforo. Cuando está a 70 m de allí se enciende la luz amarilla, cuya duración es de 4 segundos. La distancia entre el semáforo y la siguiente esquina es de 50 m.
El conductor tiene estas dos opciones: a) frenar a – 4 m/s2 o b) acelerar a + 2 m/s2. ¿Cuál de las dos opciones permite que el conductor se detenga o atraviese toda la avenida antes de que la luz cambie a rojo?
Solución
La posición inicial del conductor es x = 0 justo cuando ve la luz amarilla encenderse. Es importante convertir las unidades adecuadamente: 90 km/h equivalen a 25 m/s.
Según la opción a), en los 4 segundos que dura la luz amarilla el conductor recorre:
x(t) = vo t +½at2= 25.4 -½.(-4).42m =68 m (Se detiene 2 metros antes del semáforo)
Analizando la opción b) se tiene:
x (t) = vo t +½at2= 25.t +½.2.t2
Mientras dura la luz amarilla, el conductor recorre de esta forma:
x= 25.4 +½.2.42m = 116 m
Pero 116 m es menor que la distancia disponible para llegar a la siguiente esquina, que es 70 + 50 m = 120 m, por lo tanto no logra atravesar toda la calle antes de que se encienda la luz roja. La acción recomendable es frenar y quedarse a 2 metros del semáforo.
A diario las personas experimentan los efectos de la aceleración: cuando viajan en coche o en autobús, ya que estos continuamente necesitan frenar y acelerar para adaptar la marcha a los obstáculos del camino. También se experimenta la aceleración cuando se sube o se baja en un ascensor.
Los parques de diversiones son sitios donde la gente paga para experimentar los efectos de la aceleración y divertirse.
En la naturaleza el movimiento rectilíneo uniformemente variado se observa cuando se deja caer libremente un objeto, o cuando se lanza verticalmente hacia arriba y se espera a que regrese al suelo. Si se desprecia la resistencia del aire, el valor de la aceleración es el de la gravedad: 9.8 m/s2.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.40-45.
- Figueroa, D. Serie Física para Ciencias e Ingeniería. Volumen 3ra. Edición. Cinemática. 69-85.
- Giancoli, D. Physics: Principles with Applications. 6th. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson. 14-18.
- Kirkpatrick, L. 2007. Física: Una mirada al mundo. 6ta Edición abreviada. Cengage Learning. 15-19.
- Wilson, J. 2011. Fisica 10. Pearson Educación. 116-119
