Ángulos suplementarios: cuáles son, cálculo, ejemplos, ejercicios
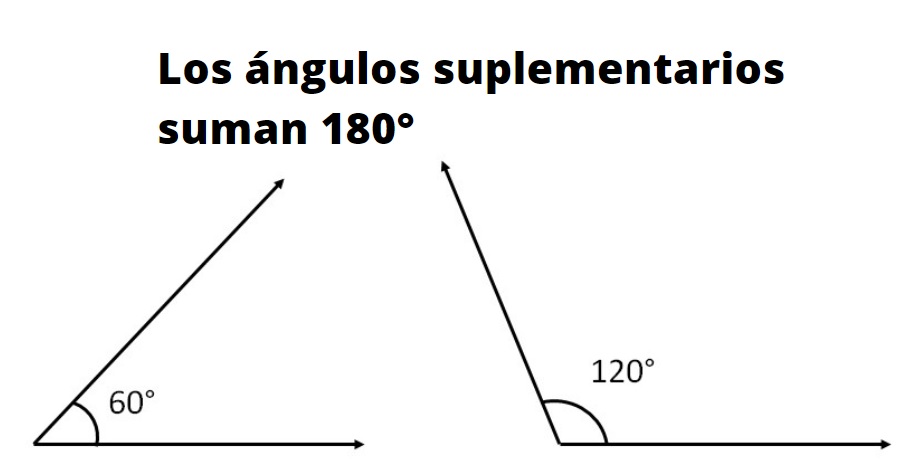
Dos o más son ángulos suplementarios si la suma de sus medidas se corresponde con la medida de un ángulo llano. La medida de un ángulo llano, también llamado ángulo plano, en grados es 180º y en radianes es π.
Por ejemplo, encontramos que los tres ángulos interiores de un triángulo son suplementarios, puesto que la suma de sus medidas es 180º. En la figura 1 se muestran tres ángulos. De lo anteriormente dicho se deduce que α y β son suplementarios, ya que son adyacentes y su suma completa un ángulo llano.
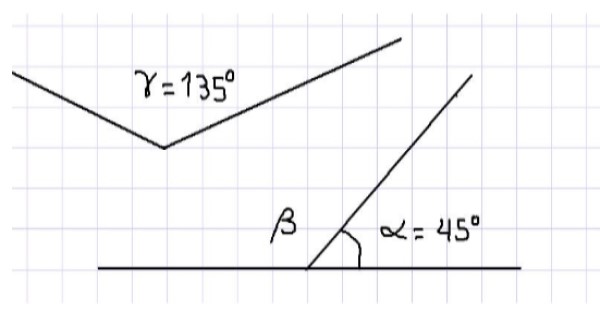
También en esa misma figura, se tienen los ángulos α y γ que también son suplementarios, porque la suma de sus medidas es igual a la medida de un ángulo plano, es decir 180º. No puede decirse que los ángulos β y γ sean suplementarios porque al ser ambos ángulos obtusos sus medidas son mayores a 90º y por tanto su suma sobrepasa 180º.
En cambio puede afirmarse que la medida del ángulo β es igual a la medida del ángulo γ, ya que si β es suplementario de α y γ es suplementario de α, entonces β = γ = 135º.
Índice del artículo
- 1 Ejemplos
- 2 Ejercicios
- 3 Ángulos suplementarios en dos paralelas cortadas por una secante
- 4 Referencias
En los ejemplos siguientes se pide encontrar los ángulos desconocidos, señalados con interrogación en la figura 2. Van desde los ejemplos más sencillos hasta algunos un poco más elaborados que el lector deberá ser con mayor cuidado.
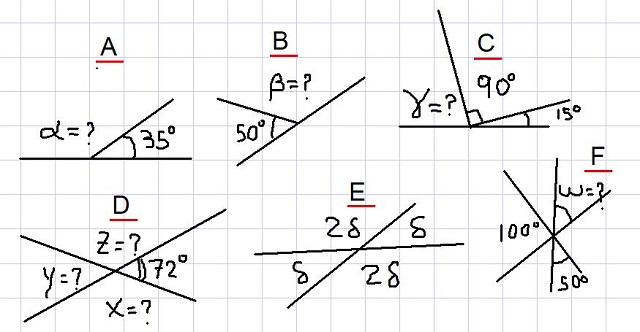
En la figura tenemos que los ángulos adyacentes α y 35º suman un ángulo plano. Es decir, α + 35º = 180º y por lo tanto se cumple que: α = 180º- 35º = 145º.
Como β es suplementario con el ángulo de 50º, entonces se sigue que β = 180º – 50º = 130º.
De la figura 2C se advierte la siguiente suma: γ + 90º + 15º = 180º. Es decir, que γ es suplementario con el ángulo 105º = 90º + 15º. Se concluye entonces que:
γ = 180º- 105º = 75º
Como X es suplementario con 72º, se deduce que X = 180º – 72º = 108º. Además Y es suplementario con X, entonces Y = 180º – 108º = 72º.
Y por último Z es suplementario con 72º, por lo tanto Z = 180º – 72º = 108º.
Los ángulos δ y 2δ son suplementarios, por lo tanto δ + 2δ = 180º. Lo cual significa que 3δ = 180º, y esto a su vez permite escribir: δ = 180º / 3 = 60º.
Si llamamos U al ángulo que está entre el de 100º y el de 50º se tiene entonces que U es suplementario a ellos dos, porque se observa que su suma completa un ángulo plano.
De inmediato se deduce que U = 150º. Como U es opuesto por el vértice a W, entonces W = U = 150º.
A continuación se proponen tres ejercicios, en todos ellos debe encontrarse el valor de los ángulos A y B en grados, de modo que se cumplan las relaciones mostradas en la figura 3. El concepto de ángulos suplementarios se emplea en la resolución de todos ellos.
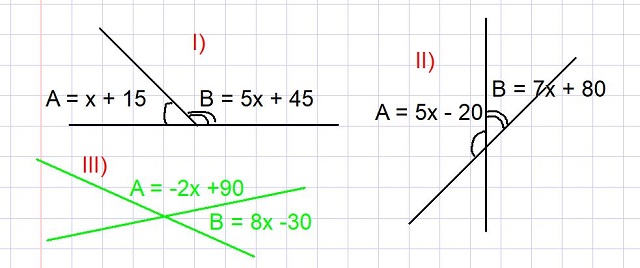
Determine los valores de los ángulos A y B de la parte I) de la figura 3.
Solución
A y B son suplementarios, de donde se tiene que A + B = 180 grados, entonces se sustituye la expresión de A y de B como función de x, tal como aparece en la imagen:
(x + 15) + (5x + 45) = 180
Se obtiene una ecuación lineal de primer orden. Para resolverla, enseguida se agrupan los términos:
6 x + 60 = 180
Dividiendo ambos miembros entre 6 se tiene:
x + 10 = 30
Y finalmente despejando, se deduce que x vale 20º.
Ahora se debe sustituir el valor de x para encontrar los ángulos pedidos. De allí se tiene que el ángulo A es: A = 20 +15 = 35º.
Y por su parte, el ángulo B es B= 5*20 + 45 = 145º.
Halle los valores de los ángulos A y B de la parte II) de la figura 3.
Solución
Como A y B son ángulos suplementarios se tiene que A + B = 180 grados. Sustituyendo la expresión de A y de B como función de x dada en la parte II) de la figura 3 se tiene:
(-2x + 90) + (8x – 30) = 180
De nuevo se obtiene una ecuación de primer grado, para la cual hay que agrupar convenientemente los términos:
6 x + 60 = 180
Dividiendo ambos miembros entre 6 se tiene:
x + 10 = 30
De donde se deduce que x vale 20º.
Es decir que el ángulo A = -2*20 + 90 = 50 º. Mientras que el ángulo B = 8*20 – 30 = 130 º.
Determine los valores de los ángulos A y B de la parte III) de la figura 3 (en color verde).
Solución
Como A y B son ángulos suplementarios se tiene que A + B = 180 grados. Hay que sustituir la expresión de A y de B como función de x dada en la figura 3, de lo cual se tiene:
(5x – 20) + (7x + 80) = 180
12 x + 60 = 180
Dividiendo ambos miembros entre 12 para despejar el valor de x, se tiene:
x + 5 = 15
Finalmente se encuentra que x vale 10 grados.
Ahora se procede a sustituir para hallar el ángulo A: A = 5*10 -20 = 30 º. Y para el ángulo B: B = 7*10 + 80 = 150º
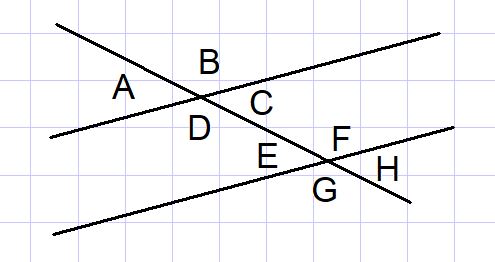
Dos rectas paralelas cortadas por una secante es una construcción geométrica habitual en algunos problemas. Entre tales rectas se forman 8 ángulos tal como lo muestra la figura 4.
De esos 8 ángulos, algunos pares de ángulos son suplementarios, los cuales enumeramos a continuación:
- Los ángulos exteriores A y B, y los exteriores G y H
- Los ángulos interiores D y C, y los interiores E y F
- Los ángulos externos A y G, y los externos B y H
- Los ángulos internos D y E, y los internos C y F
Por completitud, se nombran también los ángulos iguales entre sí:
- Los alternos internos: D = F y C = E
- Los alternos externos: A = H y B = G
- Los correspondientes: A = E y C = H
- Los opuestos por el vértice A = C y E = H
- Los correspondientes: B = F y D = G
- Los opuestos por el vértice B = D y F = G
En referencia a la figura 4, en la que muestran los ángulos entre dos rectas paralelas cortadas por una secante, determine el valor de todos los ángulos en radianes, sabiendo que el ángulo A = π/6 radianes.
Solución
A y B son ángulos externos suplementarios por tanto B = π – A = π – π/6 = 5π/6
A = E = C = H = π/6
B = F = D = G =5π/6
- Baldor, J. A. 1973.Geometría plana y del espacio. Cultural centroamericana.
- Leyes y fórmulas matemáticas. Sistemas de medida de ángulos. Recuperado de: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperado de: gutenberg.org.
- Wikipedia. Ángulos suplementarios. Recuperado de: es.wikipedia.com
- Wikipedia. Transportador. Recuperado de: es.wikipedia.com
- Zapata F. Goniómetro: historia, partes, funcionamiento. Recuperado de: lifeder.com
