Criterios de semejanza de triángulos: ejemplos, ejercicios resueltos
¿En qué consisten los criterios de semejanzas de triángulos?
Los criterios de semejanza de triángulos son las reglas que permiten conocer si dos triángulos son semejantes. La semejanza de figuras geométricas, incluyendo los triángulos, requiere que las figuras tengan igual forma, aunque no necesariamente tengan el mismo tamaño o la misma orientación.
Para que dos triángulos sean semejantes es preciso que: i) sus lados homólogos sean proporcionales y ii) los ángulos internos de cada uno tengan la misma medida.
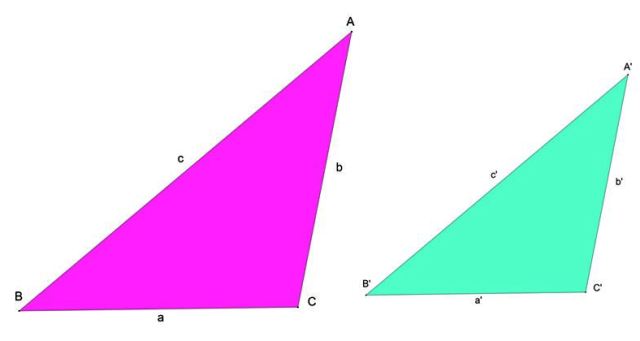
Una relación proporcional o proporción entre dos cantidades a y b se representa mediante el cociente a/b, con b ≠ 0. Para los triángulos semejantes son válidas las siguientes proporciones entre sus lados:
a/a´ = b/b´ = c/c´= r
Al valor de r se le llama razón de semejanza.
Además, los correspondientes ángulos internos tienen que ser de la misma medida, por lo tanto: ∠A =∠A´; ∠B =∠B´ y ∠C =∠C´. Según estas condiciones, los criterios de semejanza de triángulos son:
Criterio 1: dos triángulos son semejantes si tienen dos ángulos internos de igual medida. De ser así, el tercer ángulo también mide igual, ya que la suma de los ángulos internos en cualquier triángulo es 180º:
α = α´; β = β´
Criterio 2: los triángulos son semejantes si dos lados homólogos son proporcionales y el ángulo entre ellos es el mismo:
a/a´ = b/b´; α = α´
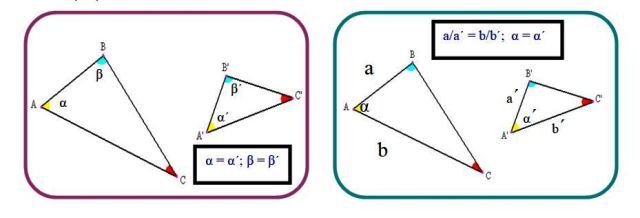
Criterio 3: los tres lados homólogos son proporcionales:
a/a´ = b/b´ = c/c´= r
Ejemplos
La semejanza de triángulos es muy útil para calcular alturas y distancias que no son fácilmente medibles de forma directa. A través de algunos cálculos sencillos, es posible averiguar estas longitudes mediante la comparación de triángulos semejantes.
Altura de columnas, edificios y árboles
Se dice que el padre de la geometría en la antigua Grecia, Tales de Mileto (625-547 a.C.), calculó la altura de la columna de un templo sin necesidad de instrumentos especiales, simplemente comparando la longitud de la sombra de su bastón con la de la columna y aplicando la semejanza de triángulos. Con el mismo método consiguió medir la altura de la Gran Pirámide de Egipto y así impresionar al faraón.
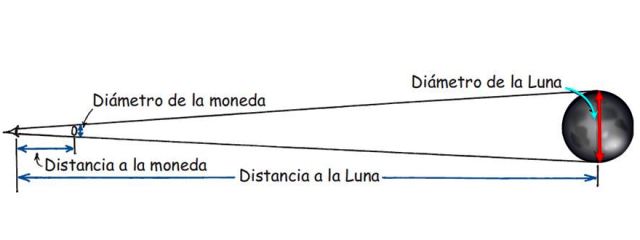
La distancia a la Luna
Hay un experimento sencillo que se hace para calcular la distancia entre la Tierra y la Luna. Requiere una moneda, un poco de cinta adhesiva y un vernier o una regla graduada. Cuando la Luna esté llena, se pega la moneda con cinta adhesiva al vidrio de una ventana y se observa la Luna con un ojo, ubicándose de manera tal que la moneda cubra justo a la Luna llena.
Cuando esto sucede, la razón entre el diámetro de la moneda y la distancia entre el ojo y la moneda, es la misma que hay entre el diámetro de la Luna y la distancia entre el ojo y la Luna:
Diámetro de la moneda/Distancia a la moneda = Diámetro de la Luna/Distancia a la Luna
La razón es aproximadamente de 1/110. Lo cual significa que la distancia a la Luna es 110 veces el diámetro de esta.
Actualmente el radio de la Luna se estima en 1737.1 km, por lo que su diámetro es 3474.2 km. Al sustituir este valor en la relación:
Distancia a la Luna = Diámetro de la Luna÷(Diámetro de la moneda/Distancia a la moneda)
Se obtiene:
Distancia a la Luna =3474.2 km÷(1/110) = 382.162 km
Muy cercano al valor establecido por los astrónomos de 384.000 km.
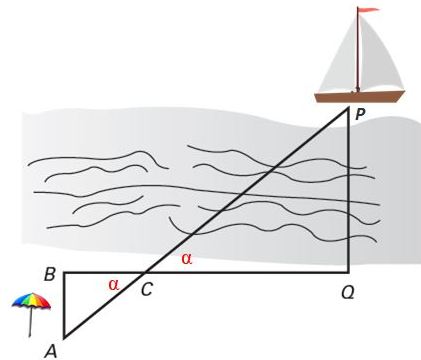
Distancia entre un barco y la orilla
Para medir la distancia entre el barco y la orilla se clavan estacas en la playa en los puntos A, B, C y Q. Los triángulos ABC y PCQ son semejantes por el criterio 1, ya que tienen dos ángulos iguales: los dos ángulos ∠C = α que son opuestos por el vértice y los dos ángulos rectos iguales a 90º: ∠B = ∠Q.
Dos triángulos ubicados de esta manera se dice que están en posición de Thales y siempre son semejantes. Se identifica a los triángulos en posición de Thales por tener un ángulo común y los lados opuestos a dicho ángulo son paralelos.
En la siguiente sección hay un ejercicio con valores numéricos.
Ejercicios resueltos
Ejercicio 1
Se quiere averiguar a qué distancia está el velero anclado de la figura anterior, de un punto Q ubicado en la orilla de la playa, para lo cual se clavan estacas en los puntos A, B, C y Q, determinando así el triángulo ABC, que es semejante a PCQ, pero cuyos lados son más fáciles de medir.
Calcular la distancia perpendicular PQ entre el barco y la orilla, mediante la semejanza de triángulos, si las distancias que se tienen son:
AB = 12 m
BC = 16 m
QC = 60 m
Solución
Las proporciones entre los lados homólogos son:
AB/QP = BC/CQ= 16 m/60 m = 0.267
Por lo tanto 0.267 es la razón de semejanza:
AB/QP = 0.267
QP = AB / 0.267 = 12 m / 0.267 = 44.9 m
Ejercicio 2
En el siguiente triángulo: ¿cuánto mide el segmento AD?
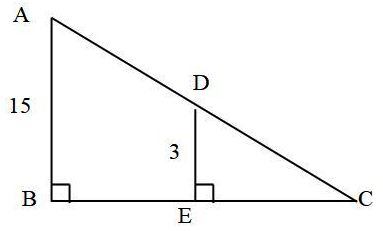
Se sabe que:
- AC = 25 cm
- AB = 15 cm
- DE = 3 cm
Solución
Los triángulos son semejantes, pues comparten un ángulo que es ∠C y los lados DE y AB son paralelos. La razón de semejanza se calcula mediante:
r = AB/DE = 15 cm / 3 cm = 5
Y también mediante:
r = AC / DC
Por lo tanto DC = AC /r = 25 cm / 5 = 5 cm
Puesto que:
AC = AD + DC
Se deduce que AD = AC – DC = 25 cm – 5 cm = 20 cm
Ejercicio 3
Un triángulo isósceles tiene un perímetro de 49 cm y una base de 21 cm. Calcular el perímetro de un triángulo semejante a este, pero cuya base mida 4 cm.
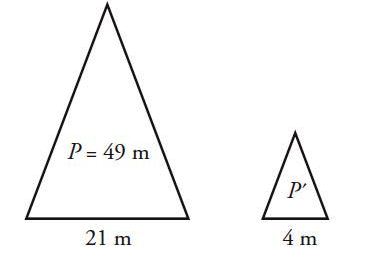
Solución
El triángulo isósceles tiene dos lados iguales, diferentes a la base b. Sea ℓ la medida de los lados y P el perímetro, que consiste en la suma de los tres lados. Para el triángulo más grande:
P = 2 ℓ + b = 49 cm
2 ℓ + 21 cm = 49 cm → ℓ = (49 -21) cm / 2 = 14 cm
Ahora se plantea la proporción entre los lados de los triángulos, los del triángulo pequeño se simbolizan con primas:
b/b´ = ℓ/ ℓ´
21 cm / 4cm = 14 cm / ℓ´→ ℓ´ = 14 cm / (21 cm / 4cm) = 2.67 cm
El perímetro del triángulo pequeño será:
P´ = 2 ℓ´ + b´ = (2 x 2.67) cm + 4 cm = 9.33 cm.
Referencias
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson.
- Clemens, S. Geometría con Aplicaciones. Addison Wesley.
- Ibáñez, P. 2010. Matemáticas III. Cengage Learning.
- Jiménez, R. Matemáticas II: Geometría y Trigonometría. 2da. Edición. Pearson.
- Stewart, J. 2007. Precálculo. 5ta. Edición. Cengage Learning.
- VicMat. Aristarco de Samos: las medidas del Sistema Solar. Recuperado de: vicmat.com
