Cuerda (geometría): longitud, teorema y ejercicios
Una cuerda, en geometría plana, es el segmento de recta que une a dos puntos de una curva. Se dice que la recta que contiene a dicho segmento es una recta secante a la curva. Con frecuencia se trata de una circunferencia, pero ciertamente se pueden trazar cuerdas en muchas otras curvas, como por ejemplo elipses y parábolas.
En la figura 1 a la izquierda hay una curva, a la que pertenecen los puntos A y B. La cuerda entre A y B es el segmento de color verde. A la derecha está una circunferencia y una de sus cuerdas, ya que es posible trazar infinitas.
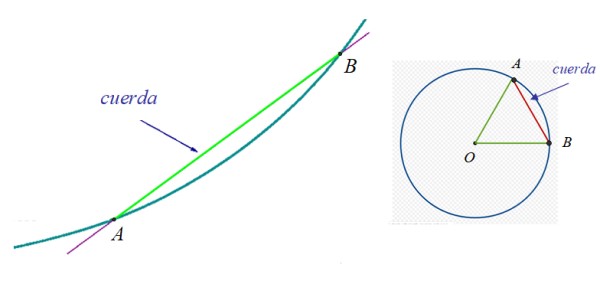
En la circunferencia es particularmente interesante su diámetro, al cual se conoce también como cuerda mayor. Se trata de una cuerda que siempre contiene al centro de la circunferencia y mide el doble del radio.
En la siguiente figura aparecen representados el radio, el diámetro, una cuerda y además el arco de una circunferencia. Identificar correctamente cada uno es importante a la hora de resolver problemas.
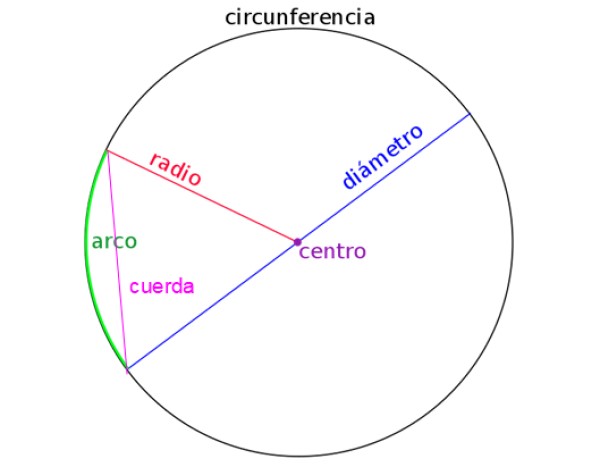
Índice del artículo
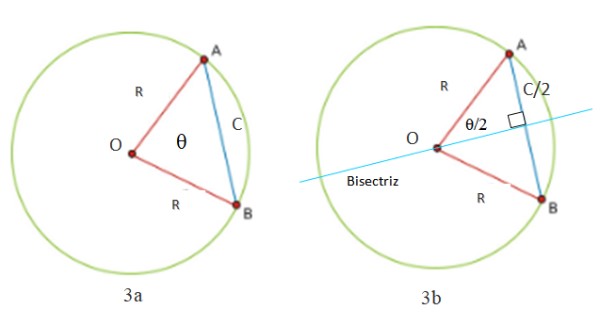
Podemos calcular la longitud de la cuerda en una circunferencia partiendo de las figuras 3a y 3b. Obsérvese que se forma siempre un triángulo con dos lados iguales (isósceles): los segmentos OA y OB, que miden R, el radio de la circunferencia. El tercer lado del triángulo es el segmento AB, llamado C, que es precisamente la longitud de la cuerda.
Es preciso trazar una recta perpendicular a la cuerda C para bisectar al ángulo θ que existe entre los dos radios y cuyo vértice es el centro O de la circunferencia. Este es un ángulo central -porque su vértice es el centro- y la recta bisectriz es también una secante a la circunferencia.
De inmediato se forman dos triángulos rectángulos, cuya hipotenusa mide R. Puesto que la bisectriz, y con ella el diámetro, divide en dos partes iguales a la cuerda, resulta que uno de los catetos es la mitad de C, tal como se indica en la figura 3b.
De la definición del seno de un ángulo:
sen (θ/2) = cateto opuesto/hipotenusa = (C/2) / R
Por lo tanto:
sen (θ/2) = C/2R
C = 2R sen (θ/2)
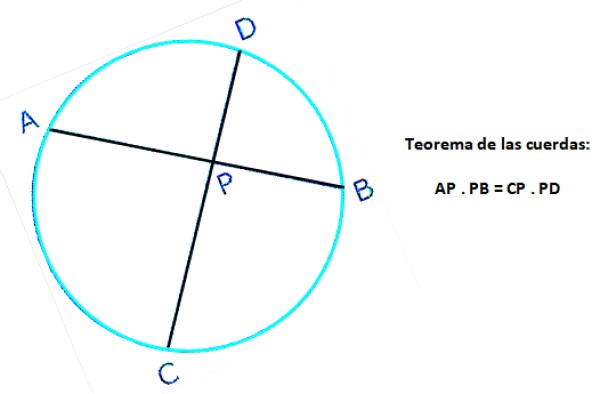
El teorema de las cuerdas dice así:
Si dos cuerdas cualesquiera de una circunferencia se intersectan en un punto, el producto de la longitud de los segmentos que aparecen en una de las cuerdas, es igual al producto de las longitudes de los segmentos que se definen en la otra cuerda.
En la siguiente figura se muestran dos cuerdas de la misma circunferencia: AB y CD, las cuales se intersectan en el punto P. En la cuerda AB se definen los segmentos AP y PB, mientras que en la cuerda CD se definen CP y PD. Entonces, según el teorema:
AP . PB = CP . PD
Una circunferencia tiene una cuerda de 48 cm, la cual dista 7 cm del centro. Calcular el área del círculo y el perímetro de la circunferencia.
Solución
Para calcular el área del círculo A, basta conocer el radio de la circunferencia al cuadrado, ya que se cumple:
A = π.R2
Ahora bien, la figura que se forma con los datos suministrados es un triángulo rectángulo, cuyos catetos son 7 y 24 cm respectivamente.
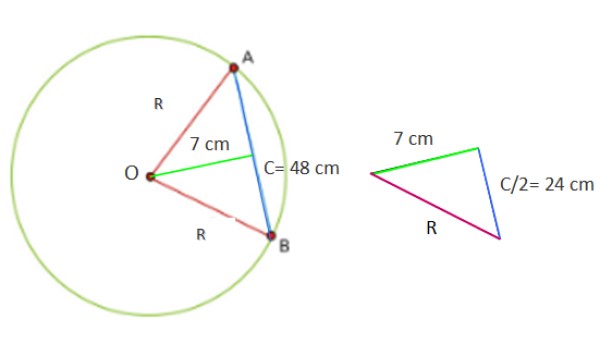
Por lo tanto para hallar el valor de R2 se aplica directamente el teorema de Pitágoras c2 = a2 + b2, ya que R es la hipotenusa del triángulo:
R2 = (7 cm)2 + (24 cm)2 = 625 cm2
Entonces el área pedida es:
A = π. 625 cm2 = 1963.5 cm2
En cuanto al perímetro o longitud L de la circunferencia, se calcula mediante:
L = 2π. R
Sustituyendo valores:
R = √625 cm2 = 25 cm
L = 2π. 25 cm = 157.1 cm.
Determinar la longitud de la cuerda de una circunferencia cuya ecuación es:
x2 + y2 – 6x – 14y -111 = 0
Se sabe que las coordenadas del punto medio de la cuerda son P (17/2 ; 7/2).
Solución
El punto medio de la cuerda P no pertenece a la circunferencia, pero los puntos extremos de la cuerda sí. El problema se puede resolver mediante el teorema de cuerdas enunciado previamente, pero antes conviene escribir la ecuación de la circunferencia en la forma canónica, para determinar su radio R y su centro O.
Paso 1: obtener la ecuación canónica de la circunferencia
La ecuación canónica de la circunferencia con centro (h, k) es:
(x-h)2 + (y-k)2 = R2
Para obtenerla es preciso completar cuadrados:
(x2 – 6x) + (y2 – 14y) -111 = 0
Obsérvese que 6x = 2.(3x) y 14y = 2.(7y), de manera que la expresión anterior se reescribe así, quedando inalterada:
(x2 – 6x+32-32) + (y2 – 14y+72-72) -111 = 0
Y ahora, recordando la definición de producto notable (a-b)2 = a2 – 2ab + b2 se puede escribir:
(x – 3)2 – 32 + (y – 7)2 – 72 – 111 = 0
= (x – 3)2 + (y – 7)2 = 111 + 32 + 72 → (x – 3)2 + (y – 7)2 = 169
La circunferencia tiene centro (3,7) y radio R = √169 = 13. La siguiente figura muestra la gráfica de la circunferencia y las cuerdas que se van a usar en el teorema:
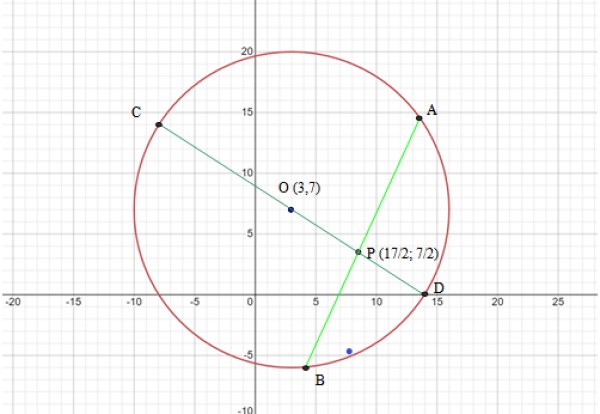
Paso 2: determinar los segmentos a utilizar en el teorema de cuerdas
Los segmentos a utilizar son las cuerdas CD y AB, de acuerdo a la figura 6, ambas se cortan en el punto P, por lo tanto:
CP . PD = AP. PB
Ahora vamos a encontrar la distancia entre los puntos O y P, ya que esto nos dará la longitud del segmento OP. Si a esta longitud le sumamos el radio, tendremos el segmento CP.
La distancia dOP entre dos puntos de coordenadas (x1,y1) y (x2,y2) es:
dOP2 =OP2 = (x2 – x1)2 + (y2 – y1)2 = (3- 17/2)2 + (7- 7/2)2 = 121/4 + 49/4 = 170 /4
dOP = OP = √170 /2
Con todos los resultados obtenidos, más la gráfica, construimos la siguiente lista de segmentos (ver figura 6):
CO = 13 cm = R
OP = √170 /2 cm
CP = OP + R= 13 + √170 /2 cm
PD = OD – OP =13 – √170 /2 cm
AP = PB
2.AP = longitud de la cuerda
Sustituyendo en el teorema de cuerdas:
CP . PD = AP . PB = [(13 +√170 /2) . (13 -√170 /2)] = AP2
[169 -170/4] = AP2
253/2 = AP2
AP = √(253/2)
La longitud de la cuerda es 2.AP = 2(√253/2) = √506
¿Podría el lector resolver el problema de otra forma?
- Baldor, A. 2004. Geometría plana y del espacio con Trigonometría. Publicaciones Cultural S.A. de C.V. México.
- C-K12. Lenght of a Chord. Recuperado de: ck12.org.
- Escobar, J. La Circunferencia. Recuperado de: matematicas.udea.edu.co.
- Villena, M. Cónicas. Recuperado de: dspace.espol.edu.ec.
- Wikipedia. Cuerda (Geometría). Recuperado de: es.wikipedia.org.
