Movimiento rectilíneo uniforme: características, fórmulas, ejercicios
El movimiento rectilíneo uniforme o a velocidad constante es aquel en el cual la partícula se mueve a lo largo de una línea recta y con velocidad constante. De esta forma el móvil recorre distancias iguales en tiempos iguales. Por ejemplo, si en 1 segundo recorre 2 metros, al cabo de 2 segundos habrá recorrido 4 metros y así sucesivamente.
Para realizar una descripción acertada del movimiento, ya sea rectilíneo uniforme o cualquier otro, es necesario establecer un punto de referencia, también llamado origen, respecto al cual el móvil cambia de posición.

Si el movimiento transcurre íntegramente a lo largo de una línea recta, interesa saber también en qué sentido el móvil la recorre.
Sobre una línea horizontal, es posible que el móvil vaya hacia la derecha o hacia la izquierda. La distinción entre ambas situaciones se hace mediante signos, siendo la convención usual la siguiente: hacia la derecha sigo (+) y hacia la izquierda signo (-).
Cuando la velocidad es constante el móvil no cambia su dirección ni tampoco su sentido, y además la magnitud de su velocidad permanece invariable.
Índice del artículo
Las principales características del movimiento rectilíneo uniforme (MRU) son las siguientes:
-El movimiento siempre transcurre a lo largo de una línea recta.
-Un móvil con MRU recorre distancias o espacios iguales en tiempos iguales.
-La velocidad permanece inalterable tanto en magnitud como en dirección y sentido.
-El MRU carece de aceleración (no hay cambios en la velocidad).
-Puesto que la velocidad v se mantiene constante en el tiempo t, la gráfica de su magnitud en función del tiempo es una línea recta. En el ejemplo de la figura 2, la recta es de color verde y el valor de la velocidad se lee sobre el eje vertical, aproximadamente +0.68 m/s.

-El gráfico de la posición x respecto al tiempo es una línea recta, cuya pendiente equivale a la velocidad del móvil. Si la recta de la gráfica x vs t es horizontal, el móvil se encuentra en reposo, si la pendiente es positiva (gráfica de la figura 3), la velocidad también lo es.

Conocer la distancia recorrida por el móvil cuando se dispone de la gráfica v vs. t es muy sencillo. La distancia recorrida equivale al área bajo la recta y comprendida dentro del intervalo de tiempo deseado.
Supóngase que se desea saber la distancia recorrida por el móvil de la figura 2 en el intervalo comprendido entre 0.5 y 1.5 segundos.
Esta área es la del rectángulo sombreado en la figura 4. Se calcula encontrando el resultado de multiplicar la base del rectángulo por su altura, cuyos valores se leen del gráfico.

Distancia recorrida = (1.5 – 0.5) x 0.68 m = 0.68 m
La distancia siempre es una cantidad positiva, sin importar si se va hacia la derecha o hacia la izquierda.
En el MRU la velocidad media y la velocidad instantánea siempre son iguales y puesto que su valor es la pendiente de la gráfica x vs t correspondiente a una recta, las ecuaciones correspondientes en función del tiempo son las siguientes:
-Posición en función del tiempo: x (t) = xo + vt
xo representa la posición inicial del móvil, en muchas ocasiones coincide con el origen del sistema de referencia, pero no siempre es así. A esta ecuación también se la conoce como ecuación itineraria.
-Velocidad en función del tiempo: v (t) = constante
Cuando v = 0 significa que el móvil está reposo. El reposo es un caso particular del movimiento.
-Aceleración en función del tiempo: a (t) = 0
En el movimiento rectilíneo uniforme no hay cambios de velocidad, por lo tanto la aceleración es nula.
Al momento de resolver un ejercicio, conviene asegurarse de que la situación se corresponde al modelo que se va a utilizar. En concreto antes de utilizar las ecuaciones del MRU es necesario cerciorarse de que son aplicables.
Los siguientes ejercicios resueltos son problemas de dos móviles.
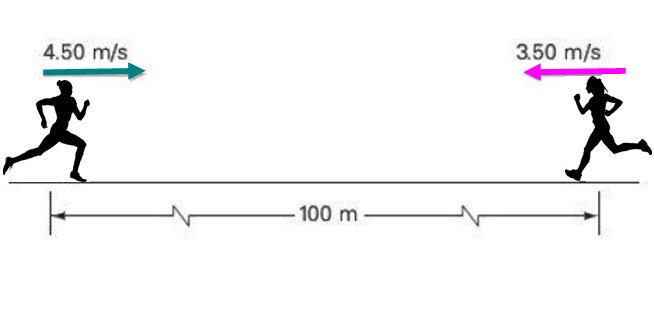
Dos atletas se aproximan una a la otra con rapidez constante de 4.50 m/s y 3.5 m/s respectivamente, estando separadas inicialmente una distancia de 100 metros, tal como indica la figura.
Si cada una mantiene su rapidez constante, encontrar: a) ¿Cuánto tardan en encontrarse? b) ¿Cuál será la posición de cada una en ese momento?
Solución
Lo primero es indicar el origen del sistema de coordenadas que servirá de referencia. La elección depende de la preferencia que tenga la persona que resuelve el problema.
Usualmente se escoge x = 0 justo en el punto de partida de los móviles, puede ser en la corredora de la izquierda o la de la derecha, incluso puede escogerse en el medio de ambas.
a) Vamos a elegir x = 0 sobre la corredora de la izquierda o corredora 1, por lo tanto la posición inicial de este es x01 = 0 y para la corredora 2 será x02 = 100 m. La corredora 1 se mueve de izquierda a derecha con velocidad v1 = 4.50 m/ mientras que la corredora 2 lo hace de derecha a izquierda con velocidad de -3.50 m/s.
Ecuación de movimiento para la primera corredora
x1 = x01 + v1t1 = 4.50t1
Ecuación de movimiento para la segunda corredora
x2 = x02 + v2t2 = 100 -3.50t2
Como el tiempo es el mismo para ambas t1 = t2 = t , cuando se encuentren la posición de ambas será la misma, por lo tanto x1 = x2. Igualando:
4.50t = 100 -3.50t
Es una ecuación de primer grado para el tiempo, cuya solución es t = 12.5 s.
b) Ambas corredoras se encuentran en la misma posición, por lo tanto esta se encuentra sustituyendo el tiempo obtenido en el apartado anterior en cualquiera de las ecuaciones de posición. Por ejemplo podemos utilizar la de la corredora 1:
x1 = 4.50t1 = 56.25 m
El mismo resultado se obtiene al sustituir t = 12.5 s en la ecuación de posición de la corredora 2.
La liebre reta a la tortuga a correr una distancia de 2.4 km y para ser justa le ofrece media hora de ventaja. En la partida, la tortuga avanza a razón 0.25 m/s, que es lo máximo que puede correr. Al cabo de 30 minutos la liebre echa a correr a 2 m/s y alcanza a la tortuga rápidamente.
Después de seguir durante 15 minutos más, piensa que tiene tiempo para echar una siesta y aun así ganar la carrera, pero se queda dormida durante 111 minutos. Cuando se despierta corre con todas sus fuerzas, pero la tortuga ya estaba cruzando la meta. Encuentre:
a) ¿Con qué ventaja gana la tortuga?
b) El instante de tiempo en que la liebre adelanta a la tortuga
c) El momento en el cual la tortuga adelanta a la liebre.
Solución a)
La carrera comienza en t = 0. La posición de la tortuga: xT = 0.25t
El movimiento de la liebre tiene las siguientes partes:
-Reposo por la ventaja que le dio a la tortuga: 0 t 30 minutos:
-Carrera para alcanzar a la tortuga y sigue corriendo un poco tras rebasarla; en total son 15 minutos de movimiento.
-Duerme durante 111 minutos (reposo)
-Despierta demasiado tarde (sprint final)
2.4 km = 2400 m
La duración de la carrera fue de: t = 2400 m/ 0.25 m/s = 9600 s = 160 min. A este tiempo le restamos 111 minutos de la siesta y 30 de ventaja, lo que hacen 19 minutos (1140 segundos). Significa que corrió durante 15 minutos antes de echarse a dormir y 4 minutos tras despertar para el sprint.
En este tiempo la liebre cubrió la siguiente distancia:
dL = 2 m/s . (15 . 60 s) + 2 m/s (4. 60 s ) = 1800 m + 480 m = 2280 m.
Como la distancia total era de 2400 metros, restando ambos valores resulta que a la liebre le faltaban 120 metros para llegar a la meta.
Solución b)
La posición de la liebre antes de quedarse dormida es xL = 2(t – 1800), considerando el retardo de 30 minutos = 1800 segundos. Igualando xT y xL encontramos el tiempo en que se encuentran:
2(t – 1800) = 0.25t
2t -0.25 t = 3600
t = 2057.14 s = 34.29 min
Solución c)
Para cuando la liebre es adelantada por la tortuga, aquella se encuentra dormida a 1800 metros desde la partida:
1800 = 0.25t
t = 7200 s = 120 min
El MRU es el movimiento más sencillo que se puede imaginar y por eso es el primero en ser estudiado en cinemática, pero muchos movimientos complejos pueden ser descritos como una combinación de este y de otros movimientos simples.
Si una persona sale de su casa y conduce hasta llegar a una larga autopista rectilínea por la cual viaja a la misma rapidez durante mucho tiempo, globalmente se puede describir su movimiento como un MRU, sin entrar en mayores detalles.
Desde luego la persona necesita dar algunas vueltas antes de entrar y salir de la autopista, pero mediante el uso este modelo de movimiento se puede estimar la duración del viaje conociendo la distancia aproximada entre el punto de partida y el de llegada.
En la naturaleza, la luz posee un movimiento rectilíneo uniforme cuya velocidad es de 300.000 km/s. Asimismo el movimiento del sonido en el aire puede suponerse rectilíneo uniforme con velocidad de 340 m/s en numerosas aplicaciones.
Al analizar otros problemas, por ejemplo el movimiento de los portadores de carga en el interior de un alambre conductor, la aproximación de MRU puede igualmente ser utilizada para dar una idea de lo que sucede dentro del conductor.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.40-45.
- Figueroa, D. Serie Física para Ciencias e Ingeniería. Volumen 3ra. Edición. Cinemática. 69-85.
- Giancoli, D. Physics: Principles with Applications. 6th. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson. 14-18.
- Kirkpatrick, L. 2007. Física: Una mirada al mundo. 6ta Edición abreviada. Cengage Learning. 15-19.
- Wilson, J. 2011. Fisica 10. Pearson Educación. 116-119.
