Circuito eléctrico mixto: qué es, características, partes, símbolos, ejemplos

¿Qué es un circuito mixto?

El circuito eléctrico mixto es aquel que contiene elementos conectados tanto en serie como en paralelo, de forma que, al cerrar el circuito, se establecen distintas tensiones y corrientes en cada uno de ellos.

Los circuitos se diseñan con una gran variedad de objetivos y sus elementos pertenecen a dos categorías: activos y pasivos.

Los elementos activos del circuito son los generadores o fuentes de voltaje o corriente, directa o alterna. Por su parte, los elementos pasivos son las resistencias, los condensadores o capacitores y las bobinas. Tanto unos como otros admiten conexiones en serie y paralelo, así como combinaciones de estas.

Otras posibles conexiones, diferentes de las asociaciones serie-paralelo, son delta (o triángulo) y estrella, de uso frecuente en máquinas eléctricas alimentadas con corriente alterna.

Características de un circuito mixto

En líneas generales, en un circuito mixto se observa lo siguiente:

• La alimentación del circuito puede ser a través de un generador directo (pila) o alterno.
• Se considera que los cables o alambres que unen los diferentes elementos no ofrecen resistencia a la corriente.
• Tanto el voltaje como la corriente pueden ser constantes o variables en el tiempo. Se utilizan las letras mayúsculas para denotar valores constantes, y las minúsculas cuando son variables.
• En los circuitos mixtos puramente resistivos, la corriente a través de las resistencias en serie es la misma, mientras que en las resistencias en paralelo en general es diferente. Para calcular la corriente y el voltaje a través de cada resistencia, usualmente se reduce el circuito a una resistencia única, llamada resistencia equivalente o R_eq .

Resistencias en serie

Resistencias en paralelo

• Si el circuito consta de n capacitores, cuando se asocian en serie la capacitancia equivalente C_eq resulta:

Capacitores en serie

Capacitores en paralelo

• Las bobinas o inductores siguen las mismas reglas de asociación que las resistencias. Así, cuando se quiere reducir una asociación de bobinas en serie para obtener la inductancia equivalente L_eq, se utilizan las siguientes fórmulas:

Inductores en serie

• Para resolver los circuitos mixtos con resistencias se utilizan la ley de Ohm y las leyes de Kirchoff. En circuitos resistivos sencillos basta con la ley de Ohm, pero para redes más complejas es preciso aplicar las leyes de Kirchoff en combinación con la ley de Ohm, además de la relación entre voltaje y corriente para capacitores y bobinas, si estos elementos también se encuentran presentes.

Relación entre el voltaje y la corriente

Dependiendo del elemento de circuito, existe una relación entre la tensión o voltaje a través del elemento con la intensidad de la corriente que pasa por él:

Resistencia R

Se emplea la ley de Ohm:

v_R(t) = R∙i_R(t)

Capacitor C

Inductancia L

Partes de un circuito mixto

En un circuito eléctrico se distinguen las siguientes partes:

Nudo

Punto de unión entre dos o más alambres conductores que conectan algún elemento activo o pasivo del circuito.

Rama

Elementos, ya sean activos o pasivos, que se encuentran entre dos nudos consecutivos.

Malla

Porción cerrada del circuito recorrida sin pasar dos veces por el mismo punto. Puede o no tener un generador de voltaje o de corriente.

Leyes o reglas de Kirchoff

Las reglas de Kirchoff se aplican tanto si las corrientes y voltajes son constantes o si son dependientes del tiempo. Aunque se las suele llamar leyes, en realidad son reglas para aplicar los principios de conservación a los circuitos eléctricos.

Primera regla

Establece el principio de conservación de la carga, al señalar que la suma de las intensidades de corriente que entran a un nudo, equivale a la suma de las intensidades que salen de él:

∑ I_entrada = ∑ I_salida

Segunda regla

En esta ocasión se establece el principio de la conservación de la energía, cuando afirma que la suma algebraica de las tensiones en una porción cerrada de circuito (malla), es cero.

∑ Vi = 0

Símbolos

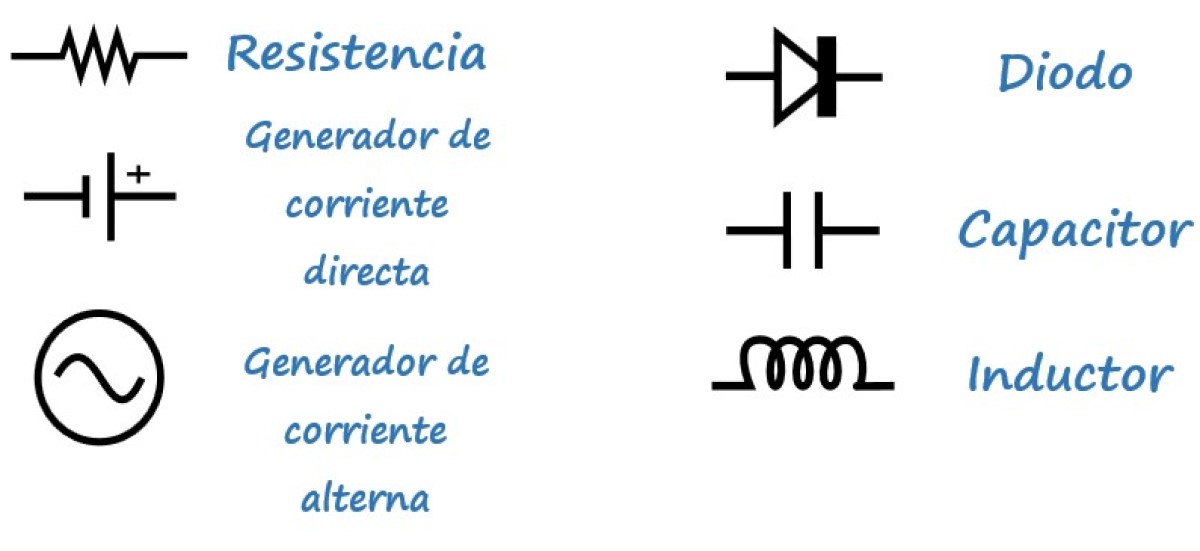
Para facilitar el análisis de los circuitos se utilizan los siguientes símbolos:

Ejemplos de circuitos mixtos

Ejemplo 1

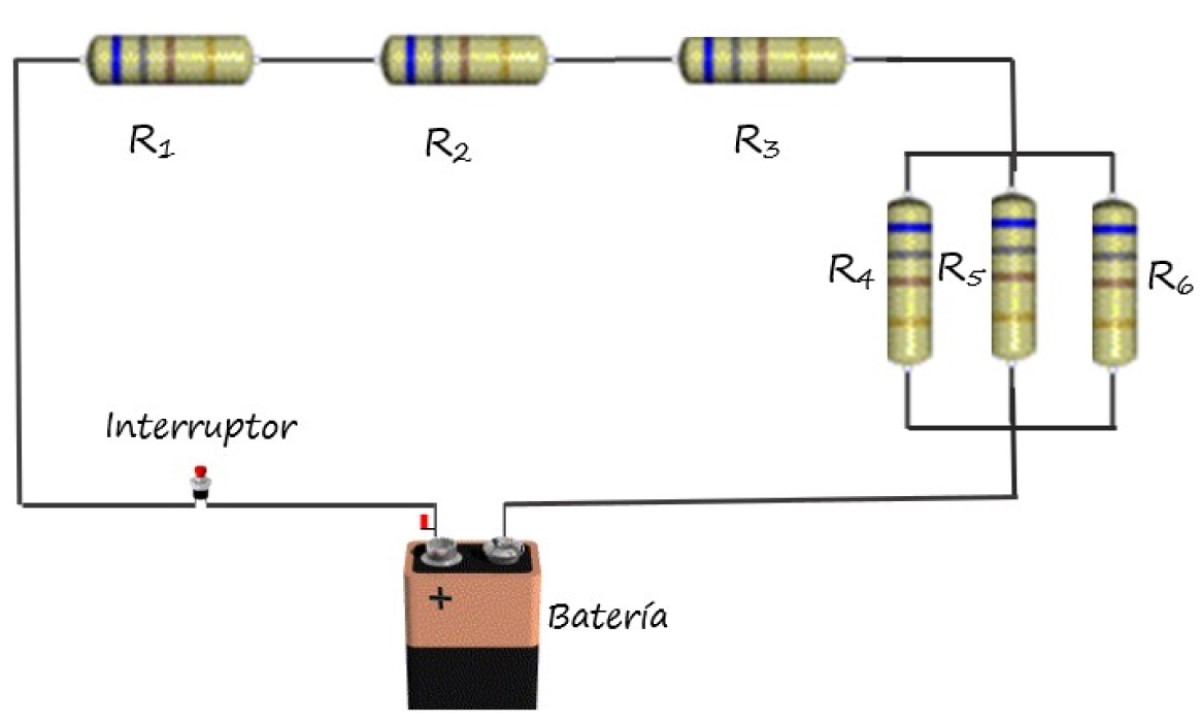
Dibujar el circuito mixto de la figura del comienzo en forma compacta, mediante el uso de los símbolos descritos arriba.

Respuesta

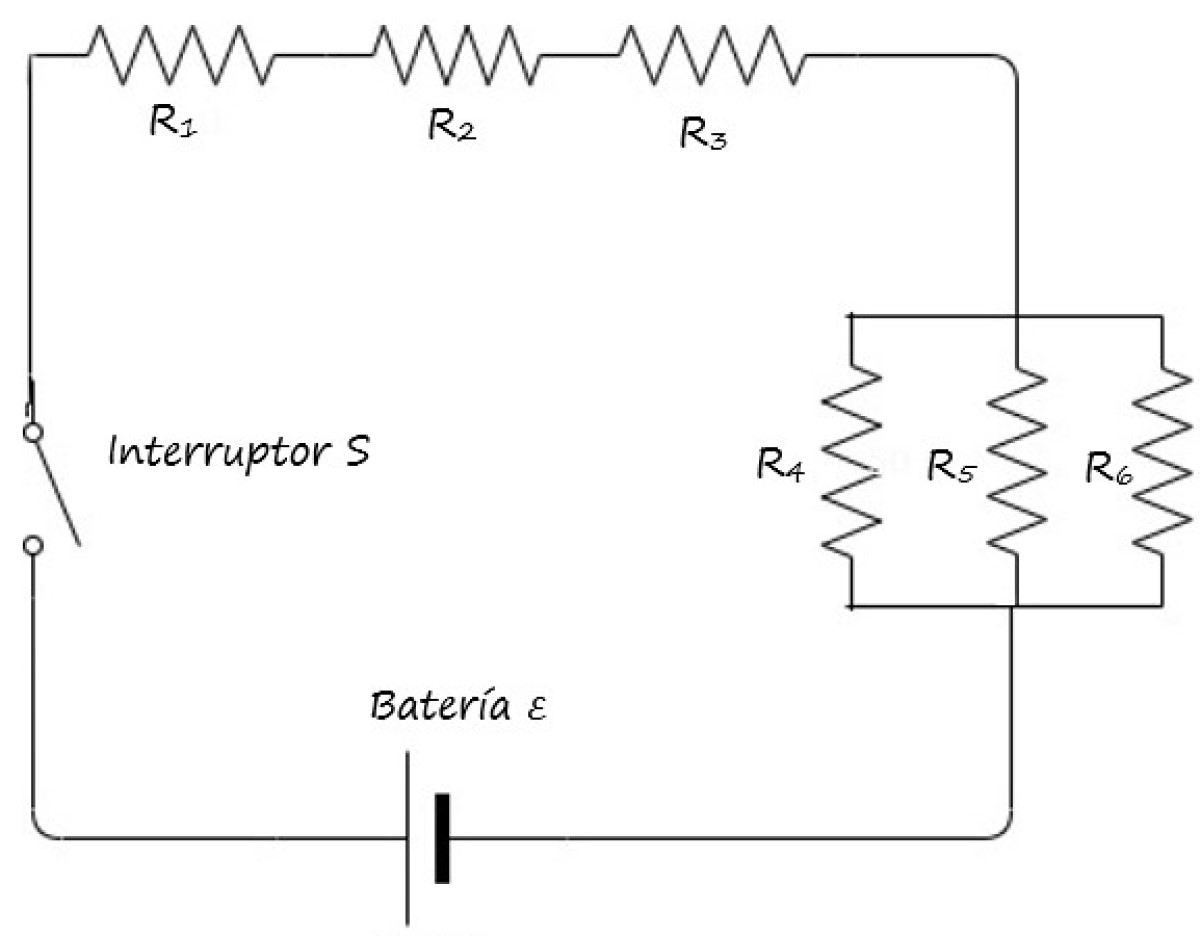
Ejemplo 2

En el circuito del ejemplo 1 se tienen los siguientes valores para las resistencias y la batería:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, R₄ = 24 Ω, R₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

Para el circuito mostrado, la batería se considera ideal, es decir, que no tiene resistencia interna. Por lo general las baterías reales tienen una pequeña resistencia interna que se dibuja en serie con la pila y se trata igual que las demás resistencias en el circuito.

Calcular lo siguiente:

• a) La resistencia equivalente del circuito.
• b) El valor de la corriente que sale de la batería.
• c) Los voltajes y corrientes en cada una de las resistencias.

Respuesta a

El primer grupo de resistencias: R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω están conectadas en serie, por lo tanto, la resistencia equivalente es R₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

En cuanto al grupo de resistencias R₄ = 24 Ω, R₅ = 48 Ω; R₆ = 48 Ω, están conectadas en paralelo y hay que aplicar la fórmula correspondiente:

R₄₅₆ = 12 Ω

El circuito simplificado que se obtiene se muestra en la siguiente gráfica, consistente en dos resistencias en serie con la pila o batería. Estas dos resistencias se suman para encontrar la resistencia equivalente del circuito original R_eq:

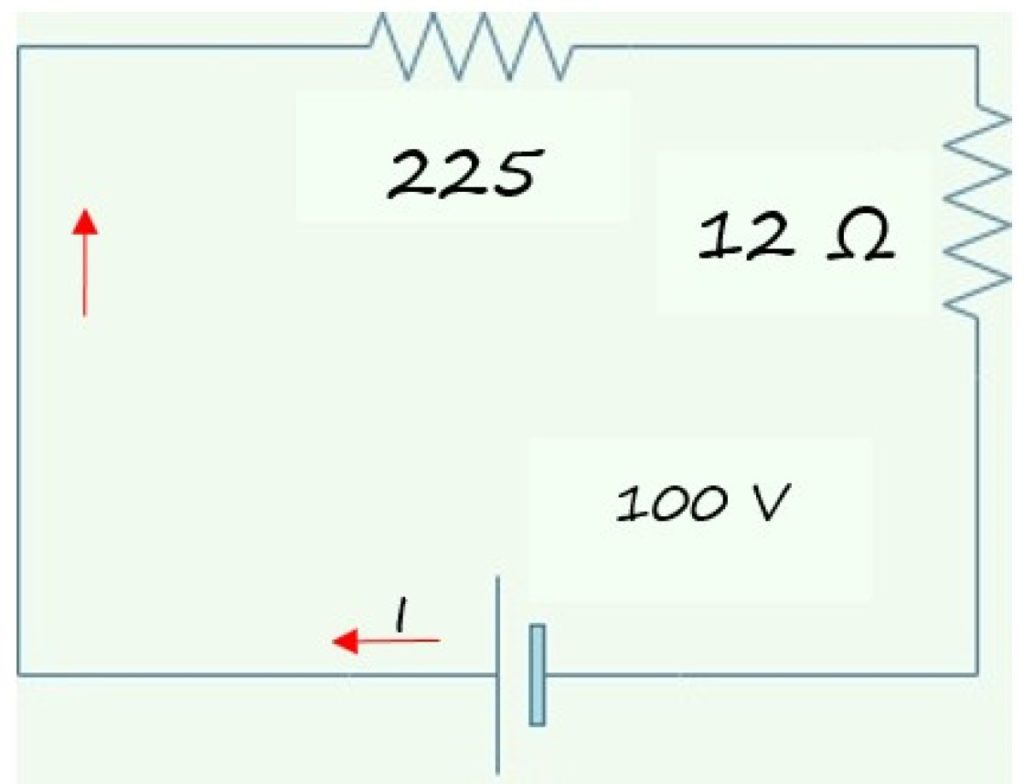
R_eq= 225 Ω + 12 Ω = 237 Ω

Respuesta b

La corriente que sale de la batería (por convención siempre se dibuja saliendo del polo postivo) se calcula con el circuito simplificado, que consiste en la resistencia equivalente R_eq en serie con la batería, al cual se le aplica la ley de Ohm:

ε = I·R

I = ε / R = 100 V / 237 Ω = 0.422 A

Respuesta c

Los voltajes y las corrientes en cada una de las resistencias sa calculan mediante la ley de Ohm. Lo primero que se observa es que la corriente que sale de la batería atraviesa totalmente las resistencias R₁ , R₂ y R₃ y en cambio, se divide al atravesar R₄ , R₅ y R₆.

Los voltajes V₁, V₂ y V₃ son:

V₁  = 0.422 A × 50 Ω = 21.1 V
V₂  = 0.422 A × 100 Ω = 42.2 V
V₃  = 0.422 A × 75 Ω = 31.7 V

Por su parte, los voltajes V₄, V₅ y V₆ tienen el mismo valor, ya que las resistencias están en paralelo:

V₄ = V₅ = V₆ = 0.422 A × 12 Ω = 5.06 V

Y las respectivas corrientes son:

I₄ = 5.06 V / 24 Ω = 0.211 A

I₅ = I₆ =5.06 V / 48 Ω = 0.105 A

Nótese que al sumar I₄, I₅ e I₆ se obtiene de nuevo la corriente total que sale de la batería.